
Tous droits réservés pour tous pays. All rights reserved.

 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
ICMC 93, Tokyo, 1993
Copyright © Ircam - Centre Georges-Pompidou 1993
This paper describes the ongoing works in the Music Representation Group at IRCAM. The general aims are stated. Then some insights are given on some specific projects such as a new quantifier, a general musical constraint satisfaction environment, and application of combinatorial optimization to musical problems.
The representation group puts a continuous development effort on PatchWork [LRD 93], a functional, common-lisp based visual programming environment which has been under design during the past three years and is now available through the new IRCAM User's Group. PatchWork has already been described in ICMC papers so we will just recall that it allows the user to go seamlessly back and forth between the Lisp programming level and the visual patch one, attention has been paid to genericity so different kind of musical objects may travel along the wires between modules, and the local states of modules can be viewed and edited through linked musical editors that offer a fairly good Common Music Notation interface.
A significant number of libraries have been designed this year including composer-specific formal systems - Bonnet, Boulez, Lindbergh, Malherbe, Messiaen, Murail, Riotte, Xenakis, among others - and music analysis ones such as an impressive model for a section of Ligeti's Melodien for orchestra by Marc Chemillier. The latter belongs to the field of formalized analysis pioneered by Riotte and Mesnage [Mesnage 88], where a computer model is build with the integral restitution of the analysed work in view when the model is submitted to simulation [Assayag 93].
PatchWork is a convenient platform for us to test new ideas and simulate prototypes of new systems, some of which will be briefly described here.
Kant is a project on rhythm quantification that has been raised by the attested failure of traditional approaches to that problem in the case we are confronted to at IRCAM : complex duration streams algorithmically generated submitted to transformation into a metrical structure in order to be integrated with other music materials prior to final instrumental writing - a different problem than quantifying an instrumental performance. Besides new formal tools such as neuronets [Desain 92] are still bounded to very simple sequences and fail to adress the higher levels of polyphony an metrics complexity.
The main ideas in our approach are :
This work is the generalization of a research done at IRCAM a few years ago by composer Claudy Malherbe and Gérard Assayag [Assayag 85]. The problem was to build from arbitrary material such as frequency analysis of complex sound objects a graph expressing harmonic relationships between objects. This graph would then be exploited when writing an instrumental score that would integrate those objects.
The idea is then to design a general tool that would help the composer to organize a database in order to build sequences optimized for any kind of relationship that he wants to reveal among objects. The underlying hypothesis is that to efficiently connect in time two musical structures whether it be such simple things as chords or more complex ones, maybe involving heterogenous materials (e.g. instruments and synthesis), one has to find a "perceptual interface", a common substructure that can be given a certain perceptual weight. This interface cans stay implicit (e.g. a common subfundamental betwenn two chords, or a sub. tactus between two rhythmic patterns) or be explicit (e.g. harmonic link between two chords). Once this is done, a graph can be built that expresses the weights of relationships between objects as well as data for later use. At this point, the idea of preferential pathes along this graph arises naturally. One would like for example to arrange a subset of the data base in order to gain a maximized expression of the relation ship (e.g. a sequence of chords that maximizes harmonic links, or joint motion between voices, etc.).
Unfortunately this is an instance of the Traveling Salesman Problem [Gilmore 92] (find a tour of a set of cities while minimizing the overall distance travelled through) which is the model for NP-complete problems (problems that no known reasonably fast algorithm can treat in general). We use an approximation of the TSP that is proved to yield a path that is no more than two times worst than the hypothetical optimal path. It runs that way:
A set of solutions can be built and compared, the freedom degrees being the choice of the tree root and the order of the children in the tree traversal.
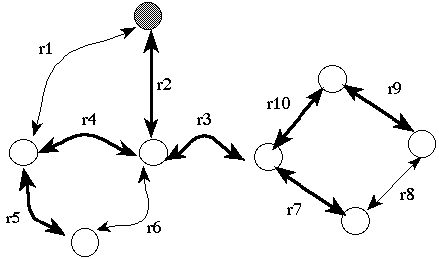
Figure 1.
The technique has been successfully tested in harmonic link optimization. An experience is being setup where the optimizing function is the joint motion between complex aggregate resulting from frequency and Terhardt analysis, the constructed data being sent to Foo (a synthesis control prototype by Gergardt Eckel) which will exploit this pre-structure in order to develop a continuous synthesis process where the voice motions will be emphasized by the effect of gain, vibrato, and any known technique of de-fusioning. Our aim there is to put the foundation for new tools that will help in the difficult problem of instruments-synthesis homogeneity.
A PIMS is the basic builduing block for generating musical material. It is defined as the structure <D, R, C> where D is a finite collection of finite sets (called Domains), R is binary relation on D and C is a set of constraints (relations) on D. Basically R is a structuring relation on D whereas elements in C are filtering relations on elements of D. Constraints in C define subsets of the cartesian product of the sets in some subset of D. Any element in the cartesian product of a constraint c is said to satisfy c. If all constraints in C define non empty sets the PIMS is said to be (locally) consistent .A PIMS in which D contains only singleton sets is called a PIMS instance . A PIMS exemplary is a consistent PIMS instance.
A partial order can be defined on PIMS's as follows: Let P=<D1, R, C> and Q=<D2, R, C> be PIMS. If any cartesian product on D1 is contained in some cartesian product on D2 then P<=Q. Given a PIMS P, the PIMS instanciation problem consists in finding a PIMS exemplary E such that E<=P. In this case E is said to be an exemplary of P. Seen from this perspective a PIMS is a structure scheme representing the set of its exemplary structures. The graph in the figure below represents a PIMS for the set of all three note chords beginning in any one of the notes in the set base (in MIDI), having consecutive intervals taken from the sets int1, int2 (in semitones), not containing octaves and positioned within the register from 60 to 79 in MIDI.
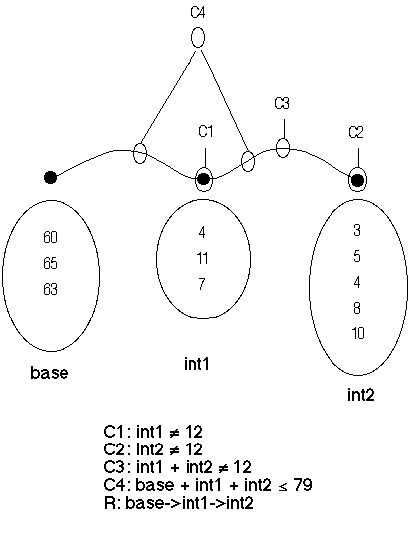
Figure 2.
Musical constraints within a PIMS are in general conceived by the composer as having different degrees of importance. We describe next a mechanism implemented in Niobé for taking account of this fact.
v(P) = minc in P [{1-a| a = importance(c) and ~satisfied(c)}U {1}].
Thus the value of PIMS instance P is equal to one minus the importance degree of the most important unsatisfied constraint c in P. The PIMS instanciation problem can then be redefined as follows: Given a PIMS P, find a PIMS instance Q<=P such that v(Q)<=v(R) for any PIMS instance R<=P. A careful formalization of this way of handling soft constraints can be found in [Schiex 92]. Algorithm AC-5 has been extended in Niobé for computing maximum valued PIMS instances.
An important issue in the design of Niobé has been to provide a user friendly layer for PIMS construction and instanciation. We describe next the implementation of a graphical interface for Niobé written in PatchWork.
(and (* 7 *) (not (* 4 4 *)).
Being represented by a PatchWork box, Niobé allows any patch to define entries for domains or constraint definition, thus taking full advantage of the visual programming aspects of PatchWork. The system and its graphical interface have been successfully employed for the generation of harmonic material for the latest piece of the composer Antoine Bonnet.
Aknowledgements
We wish to thank Georges Bloch who pointed out that the graph/TSP approach was pioneered by Schoenberg himself in his harmony Treatise [Schoenberg 49], quoting Bruckner 's "law of a shorter path". The minimization function was the harmonic link by common notes.
References
[Assayag 85] G.Assayag, M. Castellengo, C. Malherbe. "Functional integration of complex instrumental sounds in music writing." Proceedings of the ICMC. Vancouver, 1985.
[Assayag 93] G.Assayag. "CAO : vers la partition potentielle." in Les Cahiers de L'IRCAM. pp 13-41. IRCAM-Centre G. Pompidou, Paris 1993.
[Balaban 92] M. Balaban. "Music Structures: Interleaving the temporal and hierarchical aspects in Music." in: Understanding Music with AI.: Perspectives on Music Cognition. M. Balaban, K Ebcioglu and O Laske (eds).(MIT press, Cambridge, 1992).
[Desain 92] P. Desain, H. Honing. "The Quantization Problem: traditional and connexionist approaches." in M. Balaban, K. Ebcioglu, O. Laske (Eds) Undestanding Music with AI : Perspective on music cognition. pp 448-464. Cambridge, Mass.: MIT Press, 1992.
[DH 91] Y. Deville, P. Van Hentenryck "An Efficient Arc Consistency Algorithm for a Class of CSP Problems". In Proceedings of the IJCAI. 91 . Sydney, Australia, 1991.
[Gilmore 92] P.C. Gilmore, E.L. Lawler, D.B. Shmoys. "The Traveling Salesman Problem. A guided tour of combinatorial optimization" in Lawler, Lenstra, Rinnooy Kan (Eds) pp 87-143. John Wiley and sons, 1985.
[LRD 93] M. Laurson, C. Rueda, J. Duthen. "The PatchWork Reference Manual" IRCAM, 1993.
[Mackworth 77] A. Mackworth. "Consistency in Networks of Relations.". Artificial Intelligence, 8:99-118, 1977.
[Mesnage 88] M. Mesnage, A. Riotte. "Un modèle informatique d'une pièce de Stravinsky." in Analyse Musicale, 10:51-67, Paris 1988.
[Ovans 90] R. Ovans "Music Composition as a Constraint Satisfaction Problem". In Proceedings of the ICMC. 1990.
[Prim 57] R.C. Prim. "Shortest connection networks and some generalizations." Bell System Technical Journals, 36:1389-1401, 1957
[SH 91] S. Sidebotton, W. Havens "Hierarchical Arc Consistency Applied to Numeric Processing In Constraint Logic Programming". CSS-IS TR 91-06, Simon Fraser University. Burnaby, Canada, 1991.
[Schiex 92] T. Schiex "Possibilistic Constraint Satisfaction Problems or 'How to Handle Soft Constraints?'". (Personal Communication) CERT-ONERA 1992.
[Schoenberg 49] A. Schoenberg. "Traité d'harmonie". J.Claude Lattès. Paris.
[Taube 91] H. Taube. "Common Music: A Music Composition Language in Common Lisp and CLOS." Computer Music Journal 15(2):21 - 32, 1991.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .