Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved.

Introduction

Upright Piano

Modal Analysis

Modal Formalism for general viscous damping

 

 

 

Eigenvalue Problem

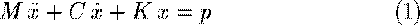
where 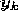can be writren as :

where 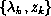are respectively the eigen values and the eigen vectors of equation(1)

Modal parameters extraction

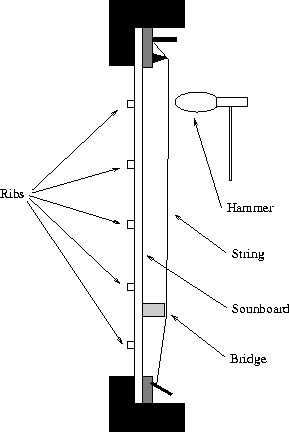
The response 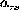at the point r to a sinusoidal excitation at the point s can be expressed using the eigen values and the eigen vectors of equation (1) :

where :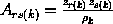 

Computation of the displacement resulting from any excitation

The displacement x(t) resulting from an excitation 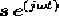can be computed using the formula :

where :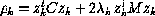

Mesasurements and Results

  
Figure 1: Modes resulting from the curve-fiting of measurements

Sound Radiation

Sound radiation of a baffled plate

The sound pressure p(r) and the acoustic velocity 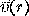resulting from the vibrations of a baffled plate moving with normal acceleration are given by :

Sound pressure radiated by the first mode of the soundboard

Active Intensity

Normal Active Intensity

The active intensity is the power radiated per unit surface.
It is given by the formula :

It is intersting to calculate the z componant of the active intensity near the soundboard in order to know which regions produce the acoustic power, in particular :

• If it is positive, the energy travels from the soundboard to the acoustic field
• If it is negative, the energy travels from the acoustic field to the sounboard.

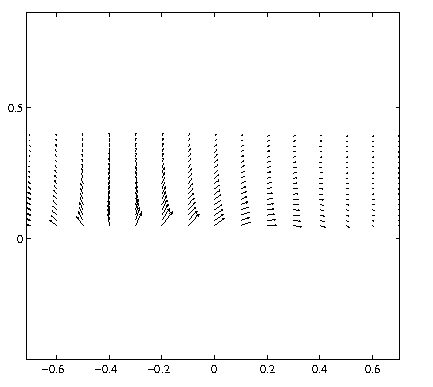
Computation of the normal Active Intensity at 5 centimeters of the soundboard

An example of a loop of active intensity

Active intensity field in a plane orthogonal to the plate for the mode 1 : 122Hz

Radiation efficiency

Power radiated

The total power radiated by a source can be computed using :

Power radiated by the soundboard versus frequency for several driving point

• Computation of the displacement of the soundboard using modal formalism
• Computation of the acoustic field
• Computation of the radiated power

Results

Radiated power for several points excited by a 1N force

Radiation efficiency

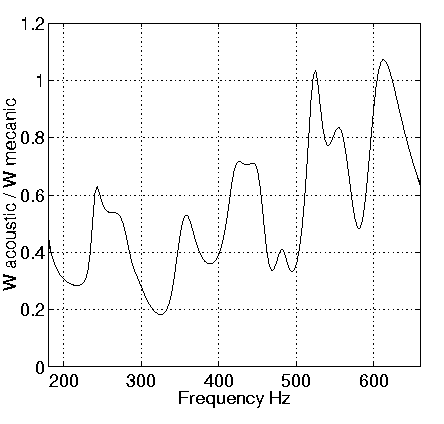
Radiation efficiency of the soundboard

Estimated radiation efficiency

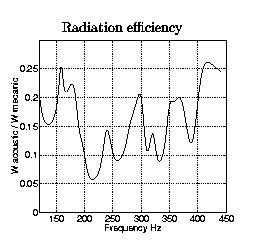
Radiation efficiency of a soundboard having eigen values (frequency and damping) a factor 1.5 higher.

Conclusion

• The first modes of the soundboard look like the ones of an isotropic suported plate
• The pressure radiated by the modes depends strongly of the position of the observer
• The frequencies of the first modes are well below the coincidence frequency of these modes
• There are loops of active Intesity
• The acoustic power depends on the location of the excitation point
• The radiation efficiency is about 15-20%

____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .

____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .