
Tous droits réservés pour tous pays. All rights reserved.

 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
ICMPC 94, Liège, 1994
Copyright © ICMPC 1994
Some authors, however, consider that the application of geometric models to dissimilarity data is not appropriate in the sense that they cannot account for certain context effect that might influence dissimilarity judgments (Tversky, 1976, Sjöberg, 1979). Tversky and Sjöberg propose classificatory models based on a conception of the similarity relation that is very different from that in geometric models. According to Tversky, the degree of similarity is defined by a matching function between the common and distinctive features of two compared objects. For Sjöberg, similarity is determined by reference to a common class and a universe, which is in turn defined by a set of mutually exclusive classes. In both conceptions, the extension of a stimulus context by the introduction of a new, different stimulus would result in an increase in the similarities among the objects that formed part of the original, "reduced" stimulus set. Tversky claims that features shared by all the objets in the original set acquire a greater "diagnosticity value" in the extended context since they are only shared by the subset of the objets drawn from the reduced context and not by the new objects in the extended context. Sjöberg proposes that the new objects may not be integrated into class of objets from the original set, which would have the effect of expanding the "universe" by the creation of new classes. He showed that the expansion of the universe results in an increase in judged similarity among objects belonging to a common class. No research to date has demonstrated such effects in a multidimensional space according to the geometric approach.
The present study investigated the possibility of such effects in the context of a geometric space. The idea is to test for these effects in a multidimensional timbre space by evaluating the influence of context changes on dissimilarity judgments between timbres. These effects should be reflected in changes in the metric distances between timbres in the geometric space as a function of the kind of contextual change. The timbre space upon which this study is based was determined by Donnadieu (1992) using 18 of the synthetic timbres employed by Krumhansl (1989) of which 12 were imitations of traditional instruments and six were hybrids. The pitch, loudness, and subjective duration of all sounds were equalized. The musical training of the 58 subjects participating in that study varied from nonmusician to professional musician. The MDS analysis used the CLASCAL model developed by Winsberg & De Soete (1993) which allows for weights on both the common dimensions and the specificities for latent classes of subjects. This analysis revealed a four-dimensional space without specificities and a single latent class of subjects. The first, second, and fourth dimensions correlated significantly with the dimensions of Krumhansl's space (attack, brightness, and spectral flux, respectively). The first and third dimensions of this space, however, were also significantly correlated. Based on this space, four contexts were constructed. Three "reduced" contexts comprised sets of timbres varying little on one of the four dimensions. Each of these contexts shared four timbres with each of the reduced contexts. The "extended" context comprised the set of 15 timbres common to all reduced contexts. According to the classificatory models, the dissimilarities between the four timbres shared by each pair of reduced contexts should be greater in the reduced contexts than in the extended context. We are also interested in knowing whether a change in context influences the dissimilarity between timbres along a single dimension (the dimension along which variation was minimized) or along several dimensions. Another hypothesis is that the minimization of variation along one of the four dimensions may cause subjects to no longer use that dimension in their evaluations of dissimilarity. According to this hypothesis, the reduce contexts would be best modeled by three-dimensional solutions and the extended context by a four-dimensional solution.
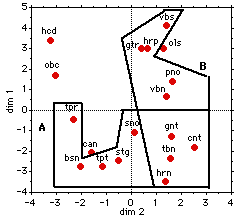
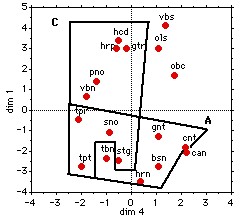
Figure 1. Timbre sets for the "reduced" contexts extracted from the four-dimensional space of Donnadieu (1992).
Procedure. The stimuli were presented diotically over a Sony Monitor K240 headset. Subjects were seated in a sound-treated room in front of the computer screen. After having read the instructions, the timbres composing the context to be tested were presented in random order to give the subject a sense of the range possible variation. Fifteen practice trials were chosen from the test context, including pairs for which the timbres had varying distances separating them in the original four-dimensional space. On each trial, a pair of timbres was presented and the subjects were asked to judge the degree of dissimilarity on a scale from 1 (very similar) to 9 (very dissimilar). The order of presentation of the sounds in the pair and the presentation order of the pairs were randomized. Each pair was presented only once in a given block. Two blocks for each context were presented within each test session. All subjects participated in four sessions corresponding to the four contexts. The presentation order of contexts A, B, and C were counterbalanced across subjects. Context D was always presented last. A mean interval of 11 days separated each session in order to reduce the possible influence of the previous context on judgments for the current context. 27 subjects participated in the experiment (15 nonmusicians and 12 musicians).
Repeated measures ANOVAs were also performed on the dissimilarity judgments for all pairs among the 9 timbres common to a given reduced context and the extended context (Pairs (36) X Context (2)). A significant effect of context was only observed for the A/D set (F(1,25)=6.1; p=.02) : dissimilarities were higher in the A context than in the D context. A significant interaction between pair and context was found for all three sets (A/D: F(35,875)=1.4; p=.05; B/D: F(35,875)=1.9; p=.001; C/D: F(35,875)=2.5; p<.0001). These interactions show that the effect of context depends on the pair of timbres being judged and may indicate differential effects of the underlying dimensions.
Multidimensional scaling with CLASCAL. According to the third hypothesis, we should observe the disappearance of one dimension in the reduced contexts. The MDS analyses for each of the three reduced contexts yield spaces in three dimensions. A four-dimensional space was found for the extended context. These results support the hypothesis.
Correlations among the dimensions of the different spaces. In order to verify that the missing dimensions in the reduced contexts corresponded to the dimensions on which the variation was minimized, correlations were performed between the positions of the timbres along each dimension of the extended and reduced contexts. According to the disappearance hypothesis, the dimensions of A should not correlate significantly with dimension 1 of the extended context. The same should hold for context B and dimension 2 of context D as well as for context C and dimension 4 of context D. The dimensions of A correlated significantly with dimensions 2, 3 and 4 of D. The dimensions of B correlated most highly with dimensions 1, 3, and 4 of D, though B's first dimension also correlated at -0.67 with D's dimension 2. The dimensions of C correlated most highly with dimensions 1, 2, and 3, thought C's dimension 2 also correlated at -0.60 with D's dimension 4. We may conclude from these results that dimension 1 of context D disappeared in context A, but that the variance along dimensions 2 and 4 in context D were only attenuated in context B and C respectively.
Analysis of context effects on the multidimensional structures. In order study the effects of context manipulation on the multidimensional structures, we examined the Euclidean distances between each of the six pairs of timbres common to a pair of reduced contexts and the extended context. The goal was to see if a change in context created by minimizing variation along a given dimension affected the distances between timbres along this dimension or along other dimensions of the space as well. This comparison requires a good correlation between the dissimilarity judgments and the Euclidean distances. The analysis reveals that all of the correlations were significant at a criterion of p=0.01 except two that were significant at p=0.05. The mean explained variance (r2) was 91.5% . The structure of relations between the four common timbres in their three possible contexts were analyzed qualitatively. In each case one of four timbres served as a reference point for lining up the structures in the different contexts for visual comparison. In general, the distances between the four timbres varied along the different dimension and not systematically along the minimized dimension. Furthermore, the distance separating the timbres along the minimized dimension was not systematically greater in context D than in the reduced contexts.
The hypothesis that a minimization of variation along one dimension should correspond to the disappearance of that dimension was verified with the qualification that in some cases the dimension seemed to be merely attenuated. In fact, the presentation of a set of timbres that vary little along a dimension leads subjects to take this dimension of variation into account to a lesser degree in their dissimilarity ratings, which does not support the predictions of the classificatory models. MDS analyses only gave three-dimensional structures for the reduced contexts and a four-dimensional structure for the expanded context. Correlations between these spaces indicate that indeed the dimension that was absent or attenuated was the minimized dimension. This effect is clearer for context A than for contexts B and C. The physical interdependence of certain dimensions in multidimensional timbre space may not allow subjects to evaluate the dissimilarities between timbres along a single one of its defining dimensions. It may be that in the case of timbre, the "brightness" and "spectral fine structure" dimensions are not separable, both being of a spectral nature. The partial correlation between the second dimension of the four-dimensional space and brightness and spectral fine structure dimensions of Krumhansl's study would argue in favor of this hypothesis. This result is partially coherent with the classificatory models, according to which a change in context should correspond to a change in the degree of similarity. In our case this would correspond not to the disappearance of a dimension but to a change in scale of the degree of similarity along the minimized dimension. In other words, the dimension considered as a succession of features should remain just as salient for the subjects. However, the dimensions tend to disappear or to be attenuated without the degree of similarity varying in a systematic fashion in the direction observed by Tversky and Sjöberg.
Grey, J.M. (1977). Multidimensional perceptual scaling of musical timbres. Journal of the Acoustical Society of America.61, 1270-1277.
Krimphoff, J. , McAdams, S. & Winsberg, S. (1994). Caractérisation du timbre des sons complexes. II : Analyses acoustiques et quantifications psychophysiques. Proceeding of 3rd French Congress Of Acoustics, Toulouse (in press).
Krumhansl, C.L. (1989). Why is musical timbre so hard to understand ? In J. Nielzen & O. Olsson (Eds.) Structure and Electroacoustic Sound and Music (pp.43-53). Amsterdam : Elsevier (Excerpta Medica 846).
Sjöberg, L. (1979). A classificatory theory of similarity. Psychological Research, 40, 223-247.
Tversky, A. (1977). Features of similarity. Psychological Review, 84, 327-352.
Winsberg, S. & Carroll, J.D. (1988). A quasi-nonmetric method for multidimensional scaling via an extended Euclidean model. Psychometrika, 53, 217-229.
Winsberg, S. & de Soete, G. (1993). A latent class approach to fitting the weighted Euclidean model, CLASCAL. Psychometrika, 58, 315-330.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .