Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved.

Wind instruments are currently described as feedback system in which a non-linear amplifier, the sound source, drives a linear filter, the pipe ^[1]. Highly simplified physical models of the clarinet and of the violin based on the method propoed by Mc Intyre, Schumacher and Woodhouse ^[2] have demonstrated that musically interesting signals could be obtained by caricatures which require only a modest computational power to produce sound in real time. The first commercial "virtual instruments" based on this principle were welcomed last year as musically very rewarding ^[3]. These models are obviously also useful as design tools for the craftsmen of conventional musical instruments. Even more simplified "source/filter" models in which the feedback from the filter towards the source is ignored, allow a considerable data compression of the speech signal in telecommunication. Better physical models of both wind instruments and of the human voice production would certainly he welcome for a wide range of applications

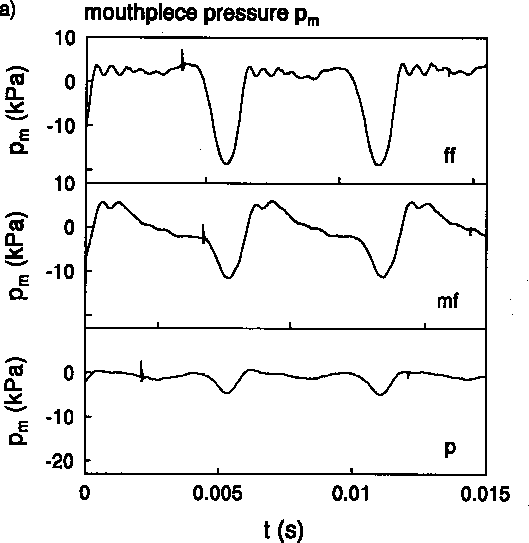
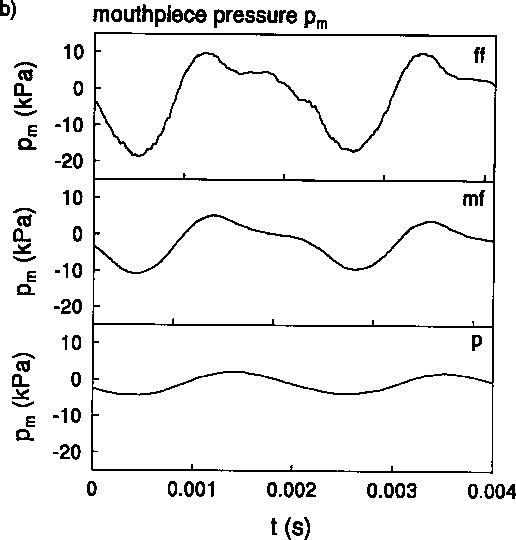
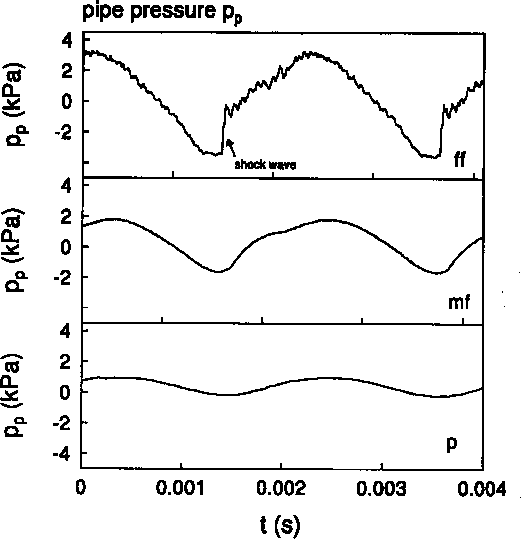
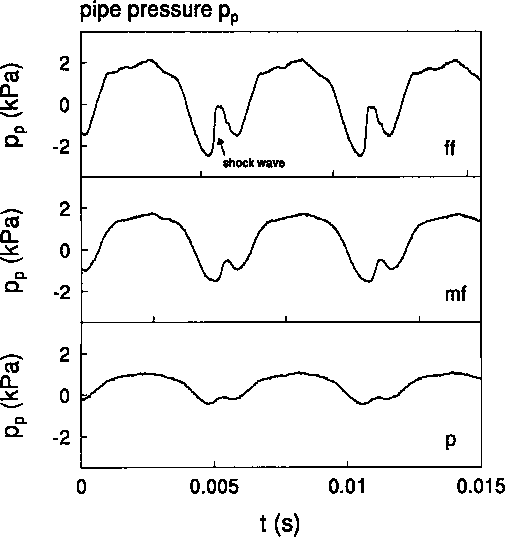
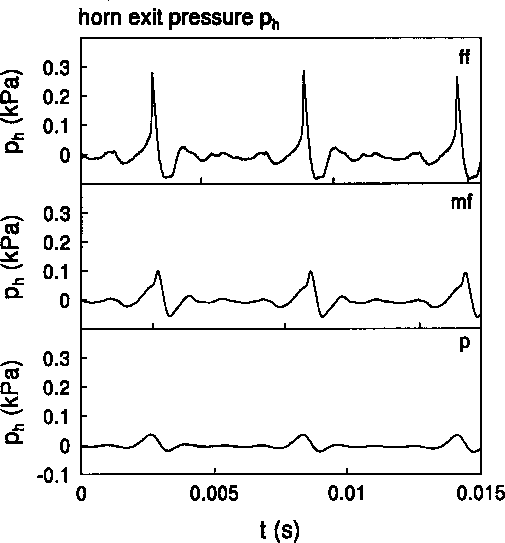
The non-linearity of the oscillator is a key aspect which is essential to reach steady oscillations in a feedback system and to determine the perceptive quality of the sound ^[1]. We focus in this paper on the hypothesis of a linear response of the pipe which has already been subject to controversy in the recent past. Backus and Hundley ^[4] report an essentially linear transfer function between the mouthpiece pressure fluctuations of an artificially blown trumpet and the radiated sound field at the listener position. Only a few per cent second harmonic generation by non-linear distortion were observed at the highest levels. These results were contradicted by later measurements of the amplitude dependency of the transfer function of a trombone by Beauchamp (^[5],^[6]). Beauchamp ^[7] had some doubt about his data, in particular the analogous tape recorder which had been used. In our experiments we used piezo electrical gauges (Kistler 603-A) with corresponding charge amplifiers (Kistler type 5007, band width lHz < f < 180kHz) for the internal pressure measurements and a l/8 inch BK condensator microphone with corresponding electronics outside the pipe. This in combination with modern electronic registration garantees the linearity and the bandwidth necessary in order to observe shock waves. Our experimental results, shown in Figure 1, confirm a violent non-linear behaviour of a trombone and provide an indication for the cause of the brightness of related brass instruments played at fortissimo levels. We observe the formation of step-wise pressure jumps. For the fortissimo level (ff) of the higher note shown in Figure 1 b), the pressurerise time corresponds to the travel time of the wave on the surface of the microphone

As we will explain further on, the non-linerity in the tranfer function depends crucially on a primary non-linearity of the source. The flow control by the lip-mouthpiece combination results into a particularly sharp presure rise during the oscillation. It is this compression phase which by non-linear wave propagation generate a shock wave. We now therefore try to understand why this occurs in a trombone while it does not occur in most instruments.

A simple explanation for the generation of this highly non-sinusoidal mouthpiece pressure p_m has been proposed for the trumpet by Backus and Hundley ^[4] and for the trombone by Elliot and Bowsher ^[8]. As shown in Figure 1 for a low pitch, the observed mouthpiece pressure signal p_m, is rather constant during much of the cycle, remaining close to the players driving pressure. This is due to the fact that the aperture between the lip is large compared to the neck of thc mouthpiece shown in Figure2: the neck controls the flow. The pressure varies sudddenly during the short time intervals in which the lips take the flow control over because they close completely. This results into the characteristic strong negative pressure pulses observed in Figure 1. This effect becomes stronger with increasing playing level. The details of the collision of the lips at closure is certainly critical. In voiced speech production ^[9] or in double red instruments ^[10] most of the radiated high frequency sound is generated in the closing phase of the "reed" movement. In contrast to this we will see that for the trombone the crucial phase of the cycle is the opening of the lips, corresponding to the compresion phase in p_m

It appears that, Backus and Hundley's mouthpiece pressure signals are dominated by much lower frequencies than our signals. Their signals do certainly not display such high pressure rise rates (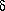p_m/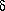t)_max as the signals we have measured. The 160dB mouth pressure amplitude reported by Backus and Hundley in their experiments, correspond to oscillation amplitudes of about 3kPa. This is much lower than our pressure fluctuations as shown in Figure 1. Also Backus and Hundley report measurements on a trumpet which can have a much shorter pipe than our trombone.

We now also can rationalize the behaviour of the pipe of the clarinet which we described earlier ^[11]. The reed channel of a clarinet is always much smaller than the pipe cross sectional area. The flow therefore is always controlled by the reed movement. In addition to this, the lay of the mouthpiece of a clarinet is curved in such a way that the reed closes gradually, the flow is never interrupted abruptly. This results into a fairly sinuoidal oscillation of the presure in the mouthpiece, even at fortissimo levels. Even though the oscillation amplitudes where comparable to lose found in the trombone, we found a very reasonable prediction of a linear model for the transfer of sound from the pipe to the listener in the case of a clarinet ^[11]. We could not even observe the non-linearities which certainly occur, for low pitches at fortissimo levels a result of vortex shedding at the pipe end and tone holes ^[12].

The very strong non-linearity of the acoustical drive of the trombone already explains much of the observed difference between the sounds of the clarinet and of the trombone. Simple models as proposed by Strong ^[13] already generate typical brass sounds but certainly not the specific brightness of the sound at fortissimo levels. This effect is controlled by the non-linear wave propagation in the pipe which we discuss now.

As the most relevant high frequencies are very efficiently radiated away at the horn, we neglect reflection at the pipe termination. We therefore can assume the propagation of a simple wave into a uniform region. Starting from the measured mouthpiece pressure p_m(t) and assuming a frictionless simple wave propagation along a pipe of uniform cross section, we can obtain an analytical prediction of the wave distortion. Thc calculation is based on the classical method of characteristics ^[14]. Due to the increase in speed of sound c with the temperature and the convective effects, the top of compression side of waves tend to catch up with the foot of thc wave. It appcars that the ratio of the pressure fluctuations p_m to the mean atmospheric pressure P^at is not the relevant parameter to judge the severity of the non-linear steepning. Theory predicts that for distance larger than the critical distance x, given by:

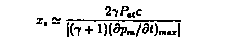
where 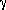= 1.4 is the Poisson constant, a shock wave is formed. The pressure profile predicted by integration along characteristics becomes multiple valued. The position and strength of this shock can be estimated from this multiple valued solution within the framework of a frictionless theory as for example the weak shock theory (^[14], ^[15]). The shock path in a (x, t) diagram is along the bisectrice of the angle formed by two characteristics of the same family which intersect in the region of multiple value solution. The weak shock speed is the mean value of the speed of the two intersecting characteristics. Equation (1) gives the first point of the shock path from which the shock path can be integrated numerically.

Even for the weak shock which we expect here, shock wave certainly correspond to a dramatic amount of high frequencies in the radiated sound: a bright "metallic" soud. As x_S, is determined by (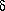p_m/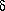t)_max we understand the importance of the initial non-linearity of the source which we discussed above.

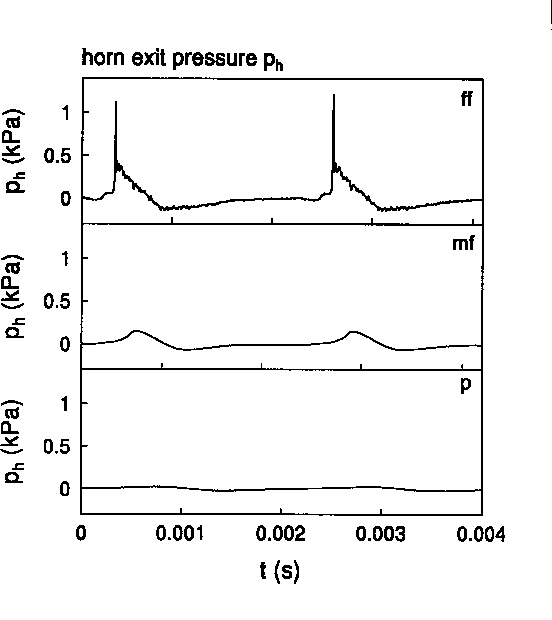
Using data shown in Figure 1 we see by using the formula for x_S that shock waves can be expected at fortissimo level because the cylindrical pipe segment in the trombone (2m to 3m) is longer than _S. Indeed in Figure 1 we see pressure discontinuities in the pressure signal measured at the end of this cylindrical pipe segment. Schlieren flow visualisation obtained with a Nanolite spark discharge (80 ns) indicates again a very sharp wave front at exit of thc horn (see Figure 2). This wave of at most a millimeter thickness corresponds to the sharp pulse in the pressure signal p^r detected by the microphone (see Figure 1). Shock waves are certainly formed in a trombone under typical playing conditions. We can also expect that non-linear wave propagation is musically relevant for thc trumpet.

It is interesting to note that "bright" instruments such as the trumpet and the trombone are different from brass instruments such as Saxhorns or Fluglehorns. The bright instruments have a cylindrical pipe segment just downstream of the mouthpiece. The conical bore of the Saxhorns implies a faster decay of the wave which reduces the non-linear wave steepening. This seems to confirm that the brightness is associated with shock wave formation.

The essential role of the cylindrical portion of the bore and the strong increase of radiation efficiency with the frequency are the important components in a simple explanation of this effect. As high frequencies are not reflected at the pipe termination they do not contribute to the regeneration of the lip oscillation. We expect that a simple linear model of the pipe taking into account at least the eight first resonances should be able to describe the lip oscillation. Once the lip movement is known, the calculated mouthpiece pressure could be used for a non-linear propagation model. In this model the mouthpiece pressure would drive a simple wave into a cylindrical bore. Weak shock theory can be used to predict the shock wave, if relevant. The calculated pressure signal at the end of the cylindrical bore would then be radiated away by a linear model of the horn, keeping by filtering the relevant audio-range of frequency, to avoid numerical problems with the shock waves.
This type of carricature is simple enough so that it could be implemented in a virtual instrument.

References

[1]

Fletcher N.H. & Rossing T.D., The Physics of Musical Intrument, Springer-Verlag, N.Y. (1991).

[2]

McItyre M.E., Schumacher R.T. & Woodhouse J., On the oscillations of musical instruments, J. Acoust. Soc. Am. 74 (1983) 1325-1345.

[3]

Rideout E., Yamaha VL1 virtual acoustic synthesiser, Keyboard June (1994) 104-118.

[4]

Backus J. & Hundley T.C., Harmonic generation in the trumpet, J. Acoust. Soc. Am. 49 (1971) 509-519.

[5]

Beauchamp J., Analysis of simultaneous mouthpiece and output waveforms, Audio Engineering Society preprint Nº 1626 (1980)

[6]

Beauchamp J., Wind instrument transfer rsponse, paper presented at the ASA meeting, Seattle, US (1990)

[7]

Beauchamp J., private communication (1990)

[8]

Elliott S.J. & Bowsher J.M., Regeneration in brass wind instruments, J.Sound and Vibration, 83 (1982) 181-217.

[9]

Pelorson X. Hirschberg A. van Hassel R.R., Wijnands A.P.J. &.; Auregan Y.,Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation, J. Acoust. Soc. Am., 9 (1994)1416-1431.

[10]

Gokhshtein A.Ya., Self-vibration of finite amplitude in a tube with a reed, Sov.Phys.Dokl., 24 (1979) 739-741.

[11]

Hirschberg A., Gilbert J., Wijnands A.P.J. & Valkering A.M.C., Musical aero-acoustics of the clarinet, J.Physique IV, Colloque C5 (1994) 559-568.

[12]

Disselhorst J.H.M. & van Wijngaarden L. , Flow in the exit of open pipes during acoustic resonance, J.Fluid Mec., 99 (1980) 293-319.

[13]

Strong W.J. & Dudley D.J., Simulation of a player-trumpet system, in proceedings of the Stockholm Musical Acoustic Conference (SMAC 93), Publications issued by the Royal Swedish Academy of Music, Nº 79 (1994) 520-524.

[14]

Pierce A.D., Acoustics, 2 th ed., Acoust. Soc. Am., N.Y. (1989).

[15]

Crighton D, Dowling A.P., Ffowcs Williams J.E., Heckl M. & Leppinton F.G. Modern Mathematical Methods In Acustics, Springer Verlag London (1992).

Acknowledgements:

Figure Captions:

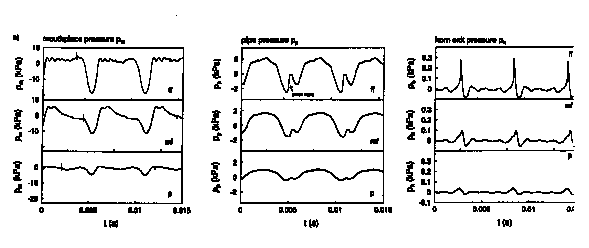
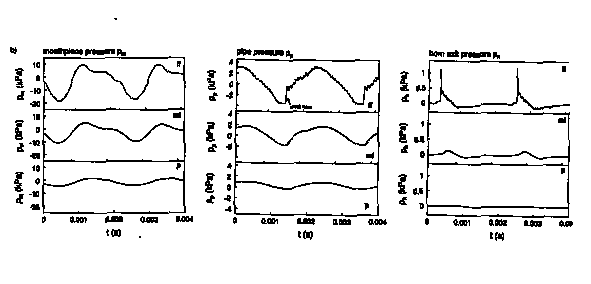
Pressure measured in the first position of a trombone for two pitches a)low and b)high at various playing levels : piano(p), mezzo-forte(mf), fortissimo(ff). We clearly observe the increased non-harmonicity of mouthpiece pressure p_m and non-linear wave steepening in the pipe pressure p_p with increasing playing level. Comparison of p_m and p_p with the pressure p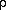 measured at the horn exit clearly demonstrate that the radiated sound is dominated by the high frequencies. The pressures p_m in the mouthpiece and p_p at the end of the cylindrical pipe section, have been measured by means of acceleration compensated piezo-electrical gages (Kistler 60A) coated with a O.lmm silicone layer to avoid thermal effects. The band-width of the filters of the charge amplifiers was 1 Hz < f < 180 kHz. 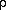An additional condensator microphone with a comparable bandwith (BK 1/8 inch.) measures the acoustical pressure p at 4.5 cm from the horn exit on the axis.

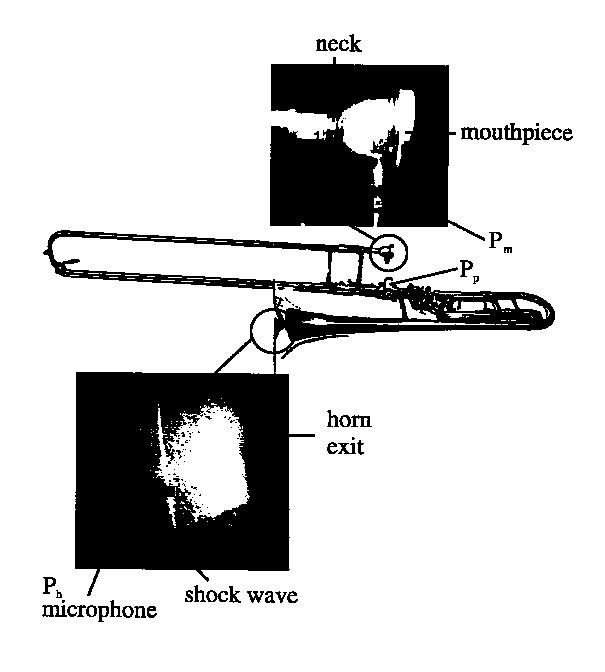
Figure 2:

A schematic representation of the trombone used in our experiments (A.Courtois trombone type 155, A. Courtois mouthpiece type 10 PM) with an indication of the position of the microphones. A typical flow visualization of a shock wave at the exit of the horn is shown. The mouthpiece geometry is specified.

____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .

____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .