Tous droits réservés pour tous pays. All rights reserved.
| Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
ICMC: International Computer Music Conference, Thessaloniki, Greece, Septembre 1997
Copyright © ICMA 1997
This paper discusses spatial sound processing algorithms and models with consideration of the following criteria: (a) naturalness and realism of the synthetic reverberation, with explicit and accurate control over the energy decay and distribution vs. time and frequency; (b) flexibility of the processing and mixing architecture with respect to the reproduction format or setup and the listening conditions; (c) computational efficiency of the system, both from the signal processing point of view and with regards to the implementation of a dynamic control interface. In conclusion, the implementation and applications of a real-time spatial sound processing software, called Spat, are described, and models for dynamically controlling early reflections and later reverberation processing parameters according to the positions and movements of the sound sources and the listener are discussed.
The traditional approach to real-time synthetic reverberation is based on delay
networks combining feedforward paths to render early reflections and feedback
paths to synthesize the later reverberation [2 - 7]. This approach cannot
guarantee the same degree of accuracy as convolution with a measured impulse
response, but provides a more efficient parametrization for dynamic control of
the synthetic reverberation effect. The use of feedback delay networks (FDNs)
for artificial reverberation can be justified fundamentally by a stochastic
model of late reverberation decays assuming that sufficient overlap (or
"density") of acoustic modes in the frequency domain and of reflections in the
time domain are achieved [2, 8]. Under these assumptions, later reflections can
be modeled as a Gaussian exponentially decaying random process, characterized
by a spectral envelope, denoted E(
), and the decay time
vs. frequency Tr() [8].
mi
to each delay unit (where mi is the delay length expressed in
samples) then has the effect of multiplying all poles by , i. e.
multiplying the reference impulse response by a decaying exponential envelope.
Frequency-dependent decay characteristics, specified by the reverberation time
vs. frequency Tr(), are obtained by use of "absorptive
filters" making each attenuation gi frequency-dependent:
where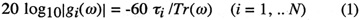
i = mi T is the delay
length expressed in seconds and T is the sample period.
An equivalent framework for reverberator design is given by digital waveguide
networks (DWNs) [5]. A DWN arises from the physical modeling of several
interconnected acoustic tubes, and is defined as a set of bi-directional delay
lines connected by "scattering junctions". A reverberator can be designed by
building a prototype DWN having lossless scattering junctions and then
introducing frequency-dependent losses [5]. The practical implementation
involves splitting each bi-directional delay line into a pair of
(mono-directional) delay units, which makes it equivalent to a FDN.
Consequently, losses can be introduced by the above method to provide explicit
control over the decay time Tr(). Conversely, any FDN can
be expressed as a DWN having a single (not necessarily physical) scattering
junction characterized by the matrix A [7].
The total delay length 
i(i)
gives the "modal density" of the artificial reverberator (average number of
eigenmodes per Hz) [2, 6, 8]. By taking
i(i) at least equal to one
fourth of the decay time, a sufficient modal overlap can be achieved [8]. With
an appropriate choice of the feedback matrix and care to avoid degenerated
cases in the distribution of delay lengths [2, 8], the impulse response can be
made indistinguishable from an exponentially decaying random Gaussian noise
with a frequency-dependent decay rate. Designing the absorptive filters
according to (1) maintains a constant frequency density along the decay by
imposing a uniform decay of all neighboring modes at any frequency, and thus
avoiding isolated "ringing modes" in the end of the reverberator's response.
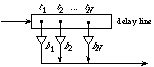
Figure 1: Basic feedback delay network
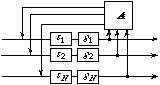
2.2 Classes of prototype networks
It can be shown [6 - 8] that a prototype network (i. e. having all poles
on the unit circle) is obtained whenever the feedback matrix A
(usually real) is unitary (or orthogonal), i. e. A*
A = I, where A* denotes the
(Hermitian) transpose of A. More generally [7], a sufficient
condition is that A be lossless, i. e. that there exist a
Hermitian, positive definite matrix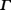 
such that
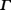A* A = 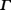(which includes unitary matrices when
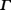= I).
The unitarity character can be defined not only for mixing matrices, but more
generally for N-input, N-output delay networks: a system is said
to be unitary if its matrix transfer function H(z) is unitary for
any complex variable z on the unit circle, (or, equivalently, if signal
energy is preserved through the system) [9]. Unitary networks are thus defined
as the multichannel equivalent of allpass filters. Similarly, one could define
a lossless network as a network having a lossless matrix transfer
function. This extension corresponds to a generalized definition of the energy
of a multichannel signal (replacing the L2 norm with the
elliptic norm induced by the matri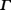x , i. e.
||x||2 = x* 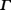x ) [7].
It has been shown [8] that any FDN whose open loop forms a unitary (or allpass) system has all of its poles on the unit circle (combining arguments in [7] and [8], it can be shown that this is also valid for lossless loops). We thus obtain a general class of prototype FDNs for artificial reverberation by applying feedback around any allpass or unitary -or, more generally, lossless- delay network. Arbitrarily complex unitary networks can be built by cascading or embedding unitary or allpass networks, which provides a wide variety of prototype FDNs (exhibiting not necessarily unitary feedback matrices) [8]. Similarly, a general class of arbitrarily complex prototype networks is given by DWNs with multiple lossless scattering junctions [5, 7]. However, despite the isomorphism between FDNs and DWNs mentioned earlier, the connections between the two corresponding classes of prototype networks remain to be further studied.
The matrix A should have no null coefficients, so that the recirculation through multiple delays produces a faster increase of the "echo density" along the time response. To speed up the convergence towards a Gaussian amplitude distribution, the "crest factor" of the matrix A (ratio of largest coefficient over RMS average of all coefficients) should be minimum. Ideally, all coefficients should have the same magnitude.
Several families of unitary matrices can satisfy this criterion, while allowing to minimize the complexity of an implementation on a programmable processor. The following solutions require generally O[N log2N] numerical operations (instead of N2) for a N by N matrix, and can provide low crest factors:
To design reverberators with multiple input and/or output channels, the
prototype network should be made to behave as a "multichannel noise generator":
the set of impulse responses associated to the different input/output channel
combinations should be equivalent to a set of mutually uncorrelated white
Gaussian noises with equal variance. This can be obtained with the structure of
Fig. 1, A being a real unitary matrix [8]. The FDN can thus be
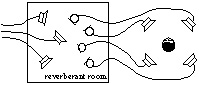
used to simulate a diffuse sound field as shown on Fig. 2, or to add
reverberation on a prerecorded multi-channel signal without affecting its
spectral content and balance.
Figure 2: Conceptual analog of multi-channel reverberator simulating
diffuse-field reverberation
where k =
2.4 Control of decay characteristics
In order to control the reverberation spectrum E()
and the decay rate Tr() independently, it is necessary to
know how the power gain of the FDN is affected by the attenuation introduced by
the absorptive filters. Assuming a unitary feedback matrix, the total power
gain of the loop is k = i(gi2), where
gi is given by (1). The power gain of the FDN is thus given
by k+k2+k3+... = k/(1-k). Consequently, the spectrum E(), the
reverberation time Tr() and the delay lengths
i can be controlled independently by inserting a
correcting filter c() in series with the FDN:
|c(
Equations (1) and (2) provide explicit control over the reverberation time
Tr()|2 = E() (1/k - 1) (2)i [ 10-6i / Tr()]
) and the spectrum E() with an
error smaller than a few percents or a fraction of a dB, respectively. The
design of each filter gi() and
c() can be optimized by a dedicated analysis-synthesis
procedure to simulate the diffuse reverberation decay of an existing room, with
arbitrary accuracy and frequency resolution [10]. An FDN as shown on Fig. 1 can
simulate the late diffuse reverberation of a room with the same degree of
accuracy and naturalness as a reverberation technique based on convolution with
an exponentially decaying noise sample. However, FDNs offer the advantage of
providing several independent input or output channels (Fig. 2) for no
additional processing cost, and dynamic control of decay characteristics
through a small set of filter coefficients.
A parametric control of the reverberation time vs. frequency can be implemented, for a wide range of applications, with simple 1rst- or 2nd-order absorptive filters [6, 8]. Biquadratic filters using 5 coefficients and designed to satisfy (1) allow control of the decay time in three independent frequency bands, with adjustable crossover frequencies. The signal-processing cost of the reverberation module of Fig. 1 is then equal to N (log2N + 7) operations per sample period (about 4 MIPS at a 48 kHz sample rate, if N = 8).
Alternately [4], the early reflections module can feed the late reverberation module without prior summing of all reflections on a single channel. This approach can be adapted as shown on Fig. 4 to provide control over the delay time and amplitude of each early reflection without affecting the tonal quality and decay characteristics of the later reverberation [8, 11]. Furthermore, in the implementation of Fig. 4, early reflections are rendered as N/2 stereo components, with left/right amplitude and time differences allowing to control their lateralization individually. The lengths of the delay units in the early and reverb modules can be easily set to adjust the overlap between the corresponding groups of reflections. The reverberator of Fig. 5 requires N (log2N + 9) numerical operations per sample period (about 5 MIPS at 48 kHz, if N = 8).
To simulate several sound sources in the same virtual room, this structure can be extended by connecting several early modules to a single reverb module [8]. Early reflection parameters can then be set differently for each source, and this will have the interesting consequence that the synthetic late reverberation responses produced associated to the individual source channels are mutually uncorrelated realizations of the same exponentially decaying random process, as would be the case for several sources placed at different positions in a real room [8].
Figure 3: Early reflections module
Figure 4: Spatial processor for two-channel stereo
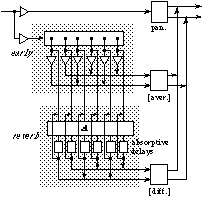
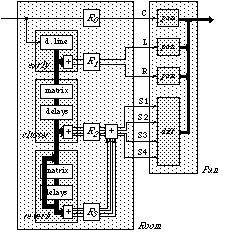
An illustration of this design method is given by the Room algorithm in
Fig. 6, which is composed of three cascaded unitary delay networks to provide
the generic room reverberation response shown on Fig. 5. The first stage is
simply an early module as previously described (Fig. 3 and 4), which can
be viewed as a 1-input, N-output unitary system (except for a scaling
factor). The cluster and reverb modules are both built by
cascading a unitary mixing matrix and a delay bank (with feedback for the
reverb module).
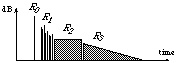
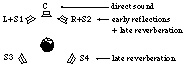
The R1 section in the impulse response (Fig. 5) contains
N/2 left reflections and N/2 right reflections adjustable in
amplitude and time. The R2 section contains
N2 reflections distributed to 4 uncorrelated channels, as is
the R3section (which has an even higher echo density). The
overlap between these different time sections is adjustable (with the only
constraint that Rn must start later than
Rn-1 and be at least as long). The total signal processing
cost of the Room module is 2N (log2N + 3) + 48,
i. e. 144 operations per sample period if N = 8, or 7 MIPS at 48 kHz,
including 3-band parametric shelving equalization for the direct sound and each
section of the reverberation, separately.
Figure 5: Generic reverberation model
Figure 6: Association of Room and Pan modules forming a
Spat processor
A complex sound scene can be synthesized by processing several individual
monophonic source signals independently and mixing the results at the output of
the respective Pan stages. A final output processing stage (denoted
Out) will generally be necessary to perform decoding and/or equalization
before feeding the loudspeaker or headphone system. The auditory sensation
experienced by the final human listener should ideally be indisguishable from
what he or she would experience if placed in the virtual sound scene at a given
position (when there are several listeners, we assume here that the acoustic
goal is the same for all of them).
2.6 Generalization - Room module
The preceding approach can be generalized to partition the impulse
response of the reverberator into several temporal sections, by (a) cascading
several unitary delay networks, (b) applying feedback to the last network and
associating an absorptive filter to each of its delay units, (c) collecting the
output signals after each stage to form the output of the reverberator.
3 Directional encoding and mixing in different formats and contexts
A spatial sound processing and mixing system can be divided into two
main signal processing stages (we assume, for the moment, a mono source signal
and a single listener). The first stage (denoted Room in Fig. 6)
synthesizes the temporal (reverberation) and spectral effects. It produces
several signals derived from the source signal and representing the direct
sound, each early reflection and the late reverberation decay (mixing these
different components into a single mono signal reconstructs the acoustic
information which would be captured by an omnidirectional microphone placed at
the notional listening position in the virtual sound scene). The second
processing stage (denoted Pan) synthesizes the directional effect
associated to each of these sound component and mixes the resulting signals in
a given multichannel output format.3.1 Directional encoding and reproduction techniques
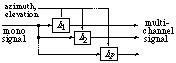
The Pan stage includes several elementary panning modules (Fig. 7) to process the direct sound and early reflections. These can be based on a
pairwise intensity panning technique [12] or emulate a multi-microphone
technique (e. g. binaural or B-format recording, or any conventional
stereophonic or quadraphonic technique). The linear filters
hi (Fig. 7), controlled by coordinates specifying the
direction of the sound, can include delays (to simulate spaced pick-up points)
and filtering (emulating the directivity of the pick-up transducers).
With an encoding technique producing direct loudspeaker feeds (pairwise
panning, conventional stereo techniques), the configuration of the loudspeaker
setup is determined at the directional encoding / mixing stage. The binaural
format and the 4-channel B-format, on the other hand, are generic
three-dimensional encoding schemes associated with decoding techniques allowing
reproduction on various loudspeaker arrangements, or headphones [13, 14, 11].
None of these 3-D sound techniques provides a superior performance to all other
techniques in all situations: the choice of the most adequate encoding format
and listening setup is based on performance and cost criteria according to the
application context (individual listening over headphones or loudspeakers,
domestic hi-fi, movie theater system, concert situation, presence of concurrent
visual cues...) [15]. Ideally, a spatial sound processing and mixing system
should be configurable to produce a mix in any of the above mentioned formats,
while the acoustic specification of the virtual sound scene should be defined
independently of the chosen format.
Figure 7: Elementary directional encoding module
Assigning to all early reflections the same direction as the direct sound would
be an excessive simplification, creating the risk of a perceived coloration of
the source signal in many cases. On the other hand, a fixed diffuse
distribution of early reflections would imply the loss of valuable directional
cues [12]. An intermediate approach consists of selecting a subset of early
reflections coming from directions close to the direct sound and adopting a
diffuse incidence approximation for other reflections. The directional group of
reflections can be rendered by producing two independent (left and right)
distributions of early reflections to form a "halo" surrounding the direction
of the direct sound. This is illustrated in Fig. 8 in the case of a frontal
sound reproduced over a 3/2-stereo loudspeaker arrangement.
This principle can be applied to any 2-D or 3-D encoding format, by panning the
left and right early reflection signals according to the direction specified
for the direct sound, so that the relative directions of the three signals are
preserved. As shown in Fig. 6, this requires only two panning modules for early
reflections, instead of one per reflection. The modularity of the system is
also improved: the Room and Pan stages now appear as two
independent modules associated in cascade. A general intermediate transmission
format is defined, comprising a center channel (C) conveying the direct sound,
two channels (L and R) conveying directional reflections, and four additional
("surround") channels conveying diffuse reflections and reverberation. The
Room module thus appears as a reverberator directly compatible with the
3/2-stereo format, while the Pan module appears as a format converter
simultaneously realizing the directional panning function.
Figure 8: Distribution of direct sound and reverberation signals on a
3/2-stereo setup (for a frontal sound).
Adopting diffuse-field normalization for all binaural synthesis filters in the
system eliminates the "diffuse" filter, and a further perceptually-based
approximation eliminates the "average" filter too [11]. The stereo spatial
processor of Fig. 4 can thus be turned into a binaural processor essentially
without modifying the reverberator itself. The only significant increase in
complexity results from replacing, in the direct sound path, the stereo panning
module by a binaural one.
Applying the inverse filtering approach to typical rooms is impractical because
it involves complex deconvolution filters and strong constraints on the
listening position. However, assuming that it is sufficient to specify the
desired room response as a distribution of energy vs. time, frequency
and direction, one can handle the equalization of the direct sound by inverse
filtering, while the remaining effects due to the reverberation of the
listening room are corrected by deconvolving echograms instead of amplitude
responses.
Rather than attempting to cancel listening room reflections, this approach
takes them into account to automatically derive optimal settings for the
synthetic reverberation parameters, so as to produce the desired target
echogram at the reference listening position. The implementation of this
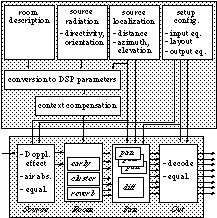
"context compensation module" (shown in Fig. 9) is simplified if the synthetic
and target reverberation -denoted R and T, respectively- are
modeled by partitioning their energy distribution in adjacent time sections
(Fig. 5) and frequency bands. The listening context is then characterized, in
each frequency band, by a set of energy weights Cijk
(representing the contribution of section Rj of the synthetic
room effect to section Tk of the target room effect, via
loudspeaker i). The coefficients Cijk are computed
off-line from echograms measured for each loudspeaker, with an omnidirectional
microphone placed at the reference listening position. The compensation is
computed in each frequency band by solving [Tk] = [Cjk] [Rj] to derive the energies
Rj (the matrix inversion is straightforward since, due to
causality, the matrix C is lower triangular). The matrix
C depends on the (azimuth and elevation) panning coordinates and
the directional reproduction technique: Cjk =
This technique (which can be extended to process live acoustic sources with
close miking) suffers from two fundamental limitations. (1) When the existing
room effect his too strong compared to the target room effect, the inversion
yields unrealizable negative energy values for some of the synthetic
reverberation parameters. This could be remedied by an improved optimization
algorithm including a positivity constraint and based on minimizing a
perceptual dissimilarity criterion. (2) Although the method allows controlling
the global intensity of early reflections at the listening position, their
temporal and directional distribution can not be controlled exactly (this would
imply extending the inverse filtering approach to early reflections). Despite
these limitations, a prototype real-time implementation (in 3 frequency bands
and 4 time sections) tested in a variable acoustic room, has confirmed that
this method allows a convincing simulation of a reverberant configuration in a
less reverberant one, without increasing the constraints on the listening
position.
Figure 9: General structure of a Spat processor
Chowning [12] introduced the principle of a higher-level perceptually-based
control interface for independent control of the angular localization and the
perceived distance r, resulting in a 2-D graphic interface for
simulating moving sources. Angular panning was applied to the direct sound and
a fraction of the reverberation, while the distance cue involved simultaneous
attenuation in intensity of the direct sound (1/r2) and the
reverberation signal (1/r) [12]. Moore's system [16] used more
sophisticated reverberation algorithms [3] and provided individual control of
each early reflection in time, intensity and direction, according to the
geometry and physical characteristics of the walls of the virtual room, the
position and directivity of each sound source, and the geometry of the
loudspeaker setup. Both of these designs involve controlling the pattern or
distribution of the reflections according to the position of the sound source,
which implies that an independent reverberation processor must be associated to
each source channel in the mixing system (or, alternatively, to each output
channel [12]).
The Spat processor of Fig. 6 presents an intermediate approach: early
reflections are handled separately from the later reverberation, yet not with
the exhaustivity of Moore's model. The software library includes several
families of elementary modules (early, cluster, reverb,
pan...) which can be combined to build reverberation and mixing systems.
The Pan and Out modules (Fig. 9) can be configured for pairwise
intensity panning, B-format, stereo or binaural encoding, with reproduction
over headphones or various 2-D or 3-D loudspeaker arrangements. The Room
module can be implemented in several versions differing in the number of
internal channels N and the flexibility of the generic model (with or
without the early and cluster modules, or sharing the
reverb module between several sources). The heaviest implementations of
a complete Spat processor according to Fig. 9 involve a theoretical
processing cost of 20 MIPS at 48 kHz, which is within the capacity of e. g. a
Motorola DSP56002.
A higher-level control interface (Fig. 9) provides a parametrization
independent from the chosen encoding format. Reverberation settings can be
derived from the analysis of measured room responses. Reverberation and
distance effects can be dynamically controlled via perceptual attributes [17,
15] (derived from earlier psycho-experimental research carried out at IRCAM),
or via physically-based statistical models. These models provide efficient
alternatives to the geometrical (image source) model [16], which entails a
prohibitive complexity for real-time tracking of source or listener movements,
unless restricted to particularly simple room geometries and only the first few
reflections.
The Spat software can be used in a wide variety of applications due to
its adaptability to various output formats and mixing configurations [15]. It
is currently implemented as a collection of modules in the FTS/Max environment,
and runs in real time on Silicon Graphics or NeXT/ISPW workstations. Since its
initial release [17], it has been used for musical composition and production
of concerts and installations, and in the post-production of CD recordings
using 3-D sound effects. Other current applications include assisted
reverberation systems for auditoria and research on human-computer interfaces,
virtual reality, and room acoustics perception.
[2] Schroeder, M. R. 1962. "Natural-sounding artificial reverberation". J.
Audio Eng. Soc. 10(3).
[3] Moorer, J. A. 1979. "About this reverberation business". Computer Music J. 3(2).
[4] Stautner, J., and Puckette, M. 1982. "Designing multi-channel
reverberators". Computer Music J. 6(1).
[5] Smith, J. O. 1985. "A new approach to digital reverberation using closed
waveguide networks". Proc. 1985 ICMC.
[6] Jot, J.-M. and Chaigne, A. 1991. "Digital delay networks for designing
artificial reverberators". Proc. 90th Conv. Audio Eng. Soc.
[7] Rochesso, D., and Smith, J. O. 1997. "Circulant and elliptic feedback delay
networks for artificial reverberation". IEEE trans. Speech & Audio 5(1).
[8] Jot, J.-M. 1992. "Etude et réalisation d'un spatialisateur de sons
par modèles physiques et perceptifs". Doctoral dissertation, Telecom
Paris.
[9] Gerzon, M. A. 1976. "Unitary (energy preserving) multi-channel networks
with feedback". Electronics Letters 12(11).
[10] Jot, J.-M. 1992. "An analysis/synthesis approach to real-time artificial
reverberation". Proc. 1992 IEEE Int. Conf. Acou. Speech and Signal Proc.
[11] Jot, J.-M., Larcher, V., and Warusfel, O. 1995. "Digital signal processing
issues in the context of binaural and transaural stereophony". Proc. 98th Conv.
Audio Eng. Soc.
[12] Chowning, J. 1971. "The simulation of moving sound sources". J. Audio Eng.
Soc. 19(1).
[13] Malham, D. G., and Myatt, A. 1995. "3-D sound spatialization using
ambisonic techniques". Computer Music J. 19(4).
[14] Cooper, D. H., and Bauck, J. L. 1989. "Prospects for transaural
recording". J. Audio Eng. Soc. 37(1/2).
[15] Jot, J.-M. 1997. "Real-time spatial processing of sounds for music,
multimedia and human-computer interfaces". Submitted ACM Multimedia Systems J.
(special issue `Audio and Multimedia').
[16] Moore, F. R. 1983. "A general model for spatial processing of sounds".
Computer Music J. 7(6).
[17] Jot, J.-M., and Warusfel, O. 1995. "A real-time spatial sound processor
for music and virtual reality applications". Proc. 1995 ICMC.
____________________________ ____________________________
3.2 Directional distribution - Pan module
Adapting the system to a given output format simply implies replacing
each elementary panning module (along with the diffuse distribution module
necessary for the late reverberation). Typically, the Pan stage should
include an individual panning module for each synthetic early reflection.
However, in a natural situation, the directions of the early reflections are
not perceived individually. This can be exploited in order to improve the
efficiency and modularity of the mixing architecture.
3.3 Binaural encoding
In the particular case of binaural encoding, the Room -
Pan structure of Fig. 6 still allows individual panning of each early
reflection, provided that this be realized in the Room module instead of
the Pan module. Although it implies a loss of modularity, this mode can
be kept as a special option for accurate auralization using binaural
techniques. However, implementing a binaural panning module requires about 140
operations per sample period, i. e. about 7 MIPS at 48 kHz (assuming that the
two directional filters h1 and h2 are both
made of a variable delay line cascaded with a 12th-order variable IIR filter)
[11].
A drastic improvement in efficiency can be obtained by introducing
perceptually-based approximations in the rendering of spectral cues for early
reflections [11]. The general approach consists of reducing the order of the
filters hi (possibly down to preserving only
frequency-independent time and amplitude interaural difference cues), and
lumping the remaining spectral cues in an "average" binaural filter (shown on
Fig. 4) for the whole set of early reflections. Similarly, the diffuse
reverberation requires a static filter simulating the "diffuse-field
head-related transfer function" as well as a 2x2 mixing matrix for controlling
the interaural cross-correlation coefficient vs. frequency.3.4 Equalization in listening rooms
For loudspeaker reproduction in anechoic conditions, all necessary
corrections can be implemented as inverse equalization filters after mixing,
and can be merged with the decoding operation in the case of transaural or
Ambisonic techniques (Out module). This includes time and spectrum
alignment of all loudspeaker channels, as well as level and spectrum
normalization between different directional encoding techniques and setups. The
only remaining discrepancies between situations then result from the intrinsic
performance of the 3-D sound techniques, in terms of localization accuracy and
robustness of the sound image according to the position of the listener. In a
practical context, however, the effects of the reverberation of the listening
room must also be considered, and compensated, if necessary, to maintain the
desired control over reverberation and distance effects, irrespective of the
listening conditions.i[sij Cijk], where
sij is the energy contribution of section
Rj in loudspeaker i.
4 Architecture and applications of a spatial sound processing software
The conventional mixing architecture, where directional localization
effects and reverberation effects are rendered by independent processing units,
implies strong limitations for interactive and immersive 3-D audio. These
relate to the heterogeneity of the control interface, the adaptation to various
reproduction formats, and the control of reverberation and distance effects
[15].5 Acknowledgments
The author would like to acknowledge the contribution of O. Warusfel
through discussions, collaboration in the experimental work, and, with J.-P.
Jullien, G. Bloch and E. Kahle, their input on perceptual and musical aspects
in the initial stages of the Spatialisateur project. This project is a
collaboration between IRCAM and Espaces Nouveaux, with the support of France
Telecom (CNET). Several aspects of this work are covered by issued or pending
patents.
References
[1] Gardner, W. G. 1995. "Efficient convolution without input-output
delay". J. Audio Eng. Soc. 43(3).
Server © IRCAM-CGP, 1996-2008 - file updated on .
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .