
Tous droits réservés pour tous pays. All rights reserved.

 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
Europhysics Letters 1 (6), pp. 295-302 (1986)
Copyright © Europhysics Letters 1986
Many musical instruments are in essence nonlinear physical systems, since their role is to convert a (quasi) constant force, pressure, etc. applied by the player into an oscillatory sound wave. For a physicist, the study of wind instruments is actually nothing but a subfield of hydrodynamics, since it amounts to studying the motion of the air inside and outside the instrument; the vibrations of the walls of the acoustical cavity are known to play a negligible role in the direct radiation of sound in the air, at least for woodwind instruments [1]. Important progress has been made recently on nonlinear hydrodynamics, instabilities, turbulence, etc. (for a review, see for example ref [2] or [3]) and one could wonder how these ideas could apply to the study of musical instruments. One specific property of wind instruments is that the nonlinearities are indeed important, but well localized-mostly in the excitation system [4, 5]; this contrasts with ordinary hydrodynamics where they are present at every point in the fluid. The aim of the present work is to study how these localized nonlinearities can drive instabilities and chaos. A related work on acoustical chaos, including sound propagation but not acoustical resonators, is described in ref. [6].
The physical study of musical instruments is not new
and much basic work was already
done in the last century [7, 8] or 50 years ago [9].
More recently, a nunber of advances in
our understanding of wind instruments have occurred;
for general reviews, see for example
ref. [4], [10] or [1]. Examples of important new results
are the studies of the role of the cut-
off frequency of hole lattices [4, 11], and of good
impedance peak co-operation [4, 12]. Here,
we take a model of the functioning of a woodwind instrument
which does not necessarily
include all these physical effects, but gives the simplest
description of nonlinear generation
of sound from a constant pressure. The model we use
draws heavily from the work published
in ref [13] and [14] (sections II-B and II-D); see in
particular the short discussion of period
doubling in appendix A of ref [14]. Among the instruments,
we choose to concentrate on the
clarinet, because it is simpler in many respects: its
acoustical cavity i approximately
cylindrical and the excitation mechanism uses a simple
reed; double reeds for the oboe or
bassoon, or flutelike excitation mechanisms are intrinsically
more complicated. A clarinet
reed is merely a thin, almost flat, flexible wedge of
cane which moves under the effect of the
pressures difference applied on both its sides (it tends
to "close" or "open"); this changes the
coupling between the applied pressure P0 inside the
mouth of the player and the pressure p
inside the acoustical resonator. A simple way to characterize
the reed is to use a nonlinear
function, f, which gives the flow of air entering the
clarinet as a function of the pressure
difference 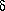 p = P0 - p; see fig. 1a). For a detailed
discussion of the shape of the curve which
gives f as a function of
p = P0 - p; see fig. 1a). For a detailed
discussion of the shape of the curve which
gives f as a function of 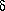 p, the reader is referred for
instance to [4] and [10]. We simply note
here that this curve includes negative (differential)
impedance parts; as is well known in
electronics for example, such negative impedances
are required to sustain permanent
oscillations.
p, the reader is referred for
instance to [4] and [10]. We simply note
here that this curve includes negative (differential)
impedance parts; as is well known in
electronics for example, such negative impedances
are required to sustain permanent
oscillations.
In the model, we include only two variables, the pressure p and the flow f, which are both functions of time t; more precisely, we define f as the flow divided by the cross-section of the cylindrical resonator (f then gives the air velocity). Since we ignore the dynamics of the reed, we simply write as a first equation
(1)
The second equation is obtained by writing a boundary condition which expresses the fact that the acoustical wave is a purely outgoing wave from the instrument (energy flows out from the bell and the open holes). If f(cL) and r() are the Fourier transforrn off(t) and p(t), this gives
Fig. 1. - a) Nonlinear characteristics of the excitation system, giving the air flow f as a function of the pressure differencep = P0 - p across the reed. When
p = pc the reed closes and f vanishes. b) Geometrical construction giving the successive values of
p and f, obtained by a nonlinear iteration using the function of a) after translation and a 45º rotation. O, 1, 2, 3 are successive iterates. F is an (unstable) fixed point. The case shown corresponds to no dissipation (
= o).
where Z(w) is the acoustical impedance of the resonator measured at a point close to the reed. If G(t) is the inverse Fourier transform of Z(w), one then obtains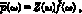
Equations (l) and (2) provide a closed system: (1) is nonlinear, but local in time; on the other hand, (2) is linear but includes multiple time delays, as we now discuss.
An idealized resonator [1] can be obtained by considering
a tube with constant section
ending on a small acoustical impedance  Z0, assumed to
be real, positive, and frequency
independent (Z0 =
Z0, assumed to
be real, positive, and frequency
independent (Z0 = 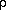 c is the acoustical impedance in
the open air). If any other source of
dissipation (viscosity, heat conduction) is ignored,
one easily obtains
c is the acoustical impedance in
the open air). If any other source of
dissipation (viscosity, heat conduction) is ignored,
one easily obtains
where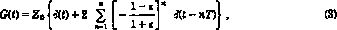
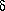 is the Dirac peak function, and T= 2L/c is the
time taken by a sound wave to travel
twice the length L of the tube. Clearly, this form
of G(t) implies multiple delays, and
complicates the solution of the problem. As discussed
in [13] and [14], an elegant way to
avoid this difficulty is to introduce two new variables
X+ and X-, the amplitudes of the
outgoing and ingoing waves:
is the Dirac peak function, and T= 2L/c is the
time taken by a sound wave to travel
twice the length L of the tube. Clearly, this form
of G(t) implies multiple delays, and
complicates the solution of the problem. As discussed
in [13] and [14], an elegant way to
avoid this difficulty is to introduce two new variables
X+ and X-, the amplitudes of the
outgoing and ingoing waves:Equation (2) then becomes:
where R(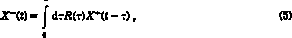
 ) is the so-called "reflexion function";
its Fourier transform R(w) is obtained from
Z(w) by the homographic transformation
) is the so-called "reflexion function";
its Fourier transform R(w) is obtained from
Z(w) by the homographic transformationFor the idealized resonator considered above, eq. (3) leads to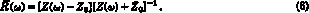
with only one time delay.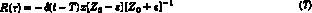
where the graph of F is obtained from that of F (with variables p and Z0f) by a 45º rotation around the origin. Now, if we set
and make use of (7), we obtain the final equation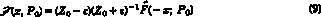
The approximations that we have made lead to a particularly simple result: the time dependence of the variable Y = - X-(t) is given by an iteration with the F function. We shall discuss here only particular solutions (it is easy to generalize), steplike solutions which remain constant and equal to Yn in any time interval nT < t < (n + 1) T, and then jump to the next value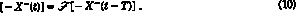
The corresponding geometrical construction is shown in fig. lb). When the time dependence of X- is obtained, equation (8) gives X+ and (4) allows one to come back to p and f. The time variations obtained in this way are similar to those shown in fig. 5 of ref. [14].
Iterations and Feigenbaum-type scenarios [15] appear
often in the study of strongly
dissipative systems [3]. This is not the case here,
since  is usually small (typically less than 0.1) and can even be put to zero.
is usually small (typically less than 0.1) and can even be put to zero.
Another difference with the usual case is that the "control parameter" P0 does not correspond to a "gain" on the nonlinear curve, but to a translation along a line at 45º to the axes. For small values of P0, the fixed point (intersection of the 45º line with the curve) i stable, since it has a slope between -1 and + 1: no oscillation occurs. When it reache the maximum of the p-f curve of fig. 1a) (that is when the differential impedance changes sign), the fixed point F become unstable: the clarinet starts to sound. The two values between which Y oscillates are obtained by intersecting the p-f curve with its symmetric with repect to the f-axes. If the curve has a steeper slope in the small pressure difference region, as in fig. 2a), small oscillations between almost equal values of Y are obtained just above threshold. On the other hand, if the opposite occurs, the bifurcation takes a different character, since the system jumps suddenly to a large level of oscillation (fig. 2b)). Fortunately, as noted by the authors of ref. [14], the f curve of real clarinets belongs to the first class of asymrnetry [4], which ensures the possibility for small oscillations and pianissirno playing.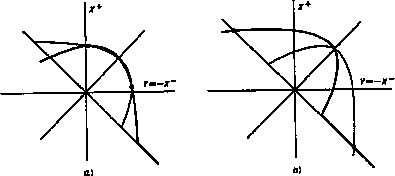
Fig. 2. - Geometrical construction of the permanent oscillation values just above threshold, obtained by intersecting the characteristic curve with its symmetric with respect to the f-axis. In fig. a), small oscillations are obtained just above threshold, but not in fig. b)
It is well known [15] that the stability of a 2-cycle of oscillations can conveniently be discussed in terms of the second iterate of F for which the 2-cycle corresponds to two stable fixed points Q and R shown in fig. 3. When the slope at these points exceeds 1 (in absolute value), the cycle becomes unstable and gives rise to a 4-cycle: a period doubling occurs in the system. Period doubling should, therefore, in principle be observable in clarinet-like systems. Nevertheless, in practice, with f-p characteristics similar to that of fig. 1a), our numerical calculations have shown that period doubling can only be obtained in a rather narrow range of the parameters, which might explain why the phenomenon does not seem to be known among real clarinet players.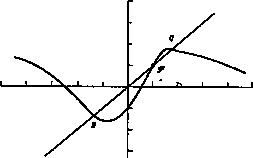
Fig. 3. - The second iterate of F;Q and R give the permanent regime of normal oscillation, until they become unstable (slope less than - l); then, period doubling occurs.
To do an experiment, it was, therefore, natural to try to obtain more flexibility on the nonlinearity introduced by the acoustical excitation system. The principle involved is shown in fig. 4; an ordinary acoustical resonator was used, in several cases a real clarinet, but the nonlinear reed excitation was replaced by an electroacoustic equivalent: a microphone measuring the acoustical pressure p inside the tube, a nonlinear system to include controlled nonlinearities in the feedback loop, and finally a loudspeaker to create a p-dependent air velocity f. The nonlinear system was either an analog electronic device, as in ref. [6], or an included digital processing of the data with a computer. The latter case gives even more flexibility on the choice of the nonlinear function, but requires using analog-digital converters, which introduces time delays (of the order of 100 µs in our experiment with two converters and the 4C computer of the IRCAM).
Figure 5 shows the results obtained in an experiment where the nonlinearity was obtained with an analog electronic circuit generating the function x3 - x; the resonator was simply a plastic tube (length: 14 cm; inner diameter: 2 cm) The results shown in fig. 5 are the Fourier spectra provided by the spectrum analyser; they correspond to increasing values of the gain in the nonlinear reaction loop. A series of three successive period doublings was obtained, the last one resulting in a very low pitch sound (70 Hz), which is very unusual with such a short resonator tube. All the period doublings could be clearly heard as sounds jumping one octave below, superimposed on some random acoustical noise, especially for the third bifurcation which is rather unstable. Beyond this bifurcation, acoustical chaos could be seen on the spectrum analyser and heard in the laboratory.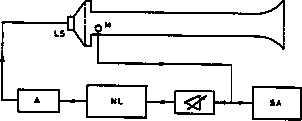
Fig. 4. - Sketch of the experimental set-up. The reaction loop includes a microphone M, a variable gain amplifier, a nonlinear system NL (either an analogic circuit or a digital device including AD converters and a computer), a power amplifier A and finally a loudspeaker LS. The signals are analysed through a spectrum analyser SA.
The number of observed period doublings might have been limited by the narrow domain of the experimental parameters in which they occur, but also by the poor efficiency of the electroacoustic components at low frequencies. The actual experiment is of course significantly different from an ideal experiment; for example phase rotations and band pass limitation are introduced by the loudspeaker. In practice, the time variations of the acoustical pressure have much smoother variations than steplike function. ALso, in the period doubling regime before the chaos limit, some random noise was already present, making the phenomenon slightly less clearly audible (and probably less interesting musically!).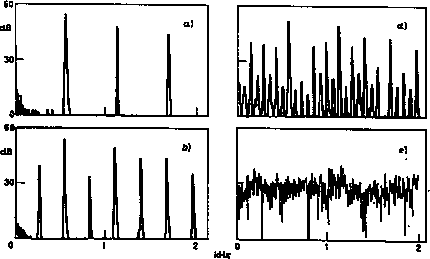
Fig. 5. - Results of our experiments showing the spectra obtained on the SA for increasing values of the gain in the feedback loop. a) Normal oscillation; b), c) (not shown) and d) are, respectively, the first, second and third period doublings; e) chaotic regime.
Similar results were also obtained with digitally generated nonlinearities, including experiments with a real clarinet (with its mouthpiece removed). In the latter case, we never obtained more than two period doublings. This is not extremely surprising with a real clarinet, the bore is not cylindrical (later holes, bell, etc.), and the reflexion function cannot be well approximated by one delta-function. We were never able to observe any period tripling in any of the experimental conditions. A more detailed report on the experimental results obtained in various situations (e.g with different sorts of nonlinearities) will be published elsewhere. A natural prolongation of these experiments would be to use several acoustical resonators in parallel, to study for example the evolution from quasi-periodic to chaotic regimes, etc.
In conclusion, although our mathematical model and the geometrical construction used in fig. 1, 2 and 3 are limited by the various simplifications on which they rely, the experiments show that the essence of their predictions for various regims of oscillations remains valid in more realistic situations, including nonideal resonators such as a real clarinet. More generally, woodwind instruments belong to a class of nonlinear systems which exihibit interesting behaviour, especially if one allows for more flexible nonlinearities. It has been known for a long time [7] that woodwind instruments can generate harmonic frequencies which do not correspond to any resonance of the resonator (e.g the even harmonics in a clarinet tone; the effect is simply a frequency doubling occuring in the nonlinear excitation). The effects observed here show that even the fundamental tone of the generated sound can also, fall at a frequency which is much below any resonance of the tube.
The authors are grateful to J. KERGOMARD and G. WEINREICH for many stimulating discussions and helpful advices.
 can be seen as a
mere (positive) convergence factor, useful to take
the
limit
can be seen as a
mere (positive) convergence factor, useful to take
the
limit 
 0+. Also, for real resonators, there are frequency-dependent
end corrections, the bore
diameter is not necessarily exactly constant, etc.,
so that the reflexion function is not a
0+. Also, for real resonators, there are frequency-dependent
end corrections, the bore
diameter is not necessarily exactly constant, etc.,
so that the reflexion function is not a 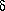 -function;
nevetheless, it has a significantly shorter memory than
G(
-function;
nevetheless, it has a significantly shorter memory than
G( ); see examples in [13].
); see examples in [13].
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .