Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved.

Abstract

We have explored some musical effects of tones with nonharmonic partials. The spacing of partials can be stretched so that each partial frequency F_IJ present in tones sounded singly or together is given by

F_IJ = A^{(I/12 + log}2^J)

Here I is the scale step in half tones, J is the partial number and A is the frequency ratio of a pseudo-octave (A = 2 for a true octave). We find that subjects can match the keys of stretched (A = 2.4) as well as unstretched passages. Stretched cadences (A = 2.4) do not seem final. But, a stretched "cadence" with equally spaced partials that goes from closely-spaced (tonally dissonant) to widely-spaced (tonally consonant) partials does seem final. Our experiments do not decide finally among three views of harmony : that harmony depends on a fundamental bass or periodicity pitch (Rameau), that harmony depends on the spacing of partials (Helmholtz and Plomp) or that harmony is a matter of brainwashing.

Introduction

All stringed and blown instruments have partials whose frequencies are harmonic or nearly harmonic ; that is, the ratios of the frequencies present in the tone are close to 1, 2, 3, 4, 5, 6, etc. times the frequency of the lowest partial, sometimes called the fundamental. It is commonly held that consonance, dissonance and harmony are associated with this integral relationship among the frequency components which make up musical tones. Indeed, nonharmonic tones, such as those of bells and gongs, do not lend themselves well to harmonic combinations, even though they add a pleasant clangor to the sound of an orchestra.

By using a computer to generate sounds, one can produce tones which include partials of any chosen frequencies.¹ This raises an important question : can tones with nonharmonic partials be used in attaining useful musical effects similar to but different from those of conventional harmony ? Our experiments were intended to give a better understanding of the subjective basis of harmony and to explore the musical use of sounds with nonharmonic partials, both sounds with "stretched" partials ² and sounds with "uniformly spaced" partials. ³

I. Theories of Harmony

Helmholtz's work has been added to by that of others. Particularly, Plomp and Levelt found in 1965 that two (or more) partials that lie within what is called a critical bandwidth produce an unpleasant sensation (unless they differ very, very little in frequency). ⁵ For frequencies above, say, 500 Hz, a critical bandwidth is about 1/4 octave (a minor third). However, Plomp and Levelt were careful to call the consonance of tones whose partials are separated by more than a critical band a "tonal consonance," and not to imply that this consonance is all there is to musical harmony.

Rameau had another view of harmony. ⁶ He observed that in a major triad all frequencies present are integer multiples of a basse fundamentale or fundamental bass which, in the root position of the chord (C, E, G) lies two octaves below the root of the chord (C). Thus, if the frequency of the fundamental bass is f_o, the frequency of the root (C) is 4f_o, the frequency of the third (E) is 5f_o, and the frequency of the fifth (G) is 6f_o. Because Rameau regarded the octave as essentially an equality, he could identify the fundamental bass of the chord with its root.

Neither Rameau nor Helmholtz knew of the phenomenon of residue pitch or periodicity pitch, which Schouten described in 1938. ⁷ When we are presented with harmonic partials in the absence of the fundamental, we perceive the pitch as the least common denominator of the frequencies present, that is, as the frequency of the missing fundamental. Thus, when we listen to a major triad we might well hear Rameau's fundamental bass. Terhardt has discussed this ⁸ and has demonstrated the effect. ⁹ The experiments we shall describe are relevant to the two views of harmony described above. But, one might hold that musical harmony is merely a matter of brainwashing ; that we accept combinations of tones that we have been taught are correct, and reject those that we have been taught are incorrect. We have some experimental evidence that bears on this.

II. Tones Used and Intent of Experiments

Here I is the scale step (I = 12 for an octave), J is the overtone number and A is the frequency ratio of the pseudo octave. For a true octave, A = 2 and

F_IJ = J2^I/12  (2)

we see that F_IJ gives the frequencies of harmonics of the notes of an equally tempered scale.

Within the accuracy of the equally tempered scale, major triads made up of notes of the true octave scale satisfy the criterion of Rameau ; the partials are all integer multiples of a fundamental bass. They also satisfy the criterion of Helmholtz. All lower partials either coincide or are well separated. If all the frequencies present in the triad are stretched according to (Eq.1), all the lower partials still coincide or are well separated. So, Helmholtz's criterion will be satisfied in the stretched triad. But, in the stretched triad the partial frequencies are no longer multiples of a fundamental bass frequency. There will no longer be a basis for a periodicity pitch. Rameau's criterion will not be satisfied.

To summarize the intent of our work with such stretched tones :

1. Harmonic effects which exist in stretched materials are produced by the interactions of stretched partials.
2. Harmonic effects which disappear in stretched materials are produced either by periodicity pitch or by brainwashing.
3. It is hard to separate brainwashing effects from other effects.

III. The Experiments

• The generations of stretched and unstretched materials.
• Test subjects' ability to identify the key of stretched and unstretched material.
• Test subjects' perception of "finality" of cadences for stretched and unstretched materials.
• Test subjects' perception of "finality" for unstretched materials with dissonant overtones removed.
• Test subjects' judgment of the finality of going from a totally dissonant chord with equally spaced partials to a tonally consonant chord with equally spaced partials.
• Observed difference and agreements among musicians and non-musicians as subjects.

III-1. Acoustic Description of the Materials

The amplitudes of the partials relative to the fundamental diminished at 9dB per factor of 2 in frequency ratio between the partial and the fundamental. The value 9dB per factor of 2 was selected to approximate normal musical instruments which tend to produce a spectrum which decreases faster than 6dB per octave, but not as fast as 12dB per octave.

The envelope of the notes was chosen to give a sustained sound with a moderately fast but not percussive attack, a slight diminuation (6dB) over the duration of the note, and a smooth decay.

The overall timbre can be described as a pleasant, bland, musical sound.

III-2. Key-Sensing Experiments

A test tape was prepared containing 24 test sequences. Each test sequence consists of the sequence :

XMXM_t

This sequence was selected over the more traditional MXM_t test in order to make the test slightly harder. In the MXM_t order, the cadence at the end of M is very close to the cadence at the end of X because X is a very short passage.

The 24 tests consisted of six groups :

1. 4 tests where M and M_t differed by 3 semitones, unstretched (A = 2) ;
2. 4 tests where M and M_t differed by 3 semitones, stretched (A = 2.4) ;
3. 4 tests where M and M_t differed by 1 semitone, unstretched (A = 2) ;
4. 4 tests where M and M_t differed by 1 semitone, stretched (A = 2.4) ;
5. 4 tests where M and M_t were major and minor of the same key, unstretched (A = 2) ;
6. 4 tests where M and M_t were major and minor of the same key, stretched (A = 2.4).

The test was taken by ten subjects. Five subjects (the non-musicians) had almost no experience as performers and described themselves as having little interest in music. The other five (the musicians) had extensive experience as amateur or semiprofessional musicians.

The results of the experiment are shown in Table I. We draw the following conclusions :

1. Everyone, musicians and non-musicians alike, performed at better than the chance level (50%) for both stretched and unstretched materials. Thus stretching did not destroy the ability to sense key in this test.
2. In general the larger the key change, the better was the performance.
3. Normal materials were easier to judge than stretched materials.
4. Musicians performed better than non-musicians.

III-3. Cadence Studies

All 25 chord pairs discussed in the next three sections were randomized on the test tape. Presumably the subjects used the same criteria in judging all 25.

The test was taken by 13 "musicians" and by 17 "non-musicians" defined according to the above discussed criteria. There were no apparent patterns of differences between the responses of the musicians and the non-musicians, so the results of these two groups were averaged together.

III-4. Finality of Cadences

Results are shown in Fig.3. It is clear that the unstretched cadence gave a strong sense of finality and the stretched cadence did not. The normal anticadence and the stretched anticadence were equally nonfinal. Thus, stretching seems to destroy the impression of finality in cadences. This supports Rameau rather than Helmholtz.

III-5. Is Finality Associated with Tonal Dissonance ?

In this experiment we started with a dominant seventh cadence as shown to the right in Fig.4. The horizontal lines at the left represent the tones of the two succeeding chords, the dominant seventh above and the tonic below. The dots on the lines show the position in half-steps of the seven partials that are present in each tone (1, 2, 3, 4, 5, 6, 8).

We see that in the dominant seventh chord there are five pair of partials a half step apart (very dissonant) and three pairs a whole step apart. When the circled dots are deleted, none of the remaining partials is less than a whole tone apart, and the chord sounds less dissonant. When the crossed dots are deleted as well, none of the remaining partials are less than a minor third apart and the chord sounds tonally consonant.

We note also that in the tonic chord, two partials must be deleted in order to make the least interval between partials a major second, and two more must be deleted in order to make the least interval between partials a minor third. Thus, the tonic chord itself has some tonal dissonance.

Subjects were asked to judge the finality of the dominant seventh cadences without deletion of partials, and with deletions to render the dominant seventh less tonally dissonant. The results are shown in Fig.5. All the cadences were given a very high finality rating. The removal of partials makes almost no difference in the ratings.

We should note that a musician identified the chords correctly even when partials had been deleted so as to make the least interval between the partials in the dominant seventh a minor third. We should also note that both the dominant seventh chord and the tonic chord were noticeably less harsh, less tonally dissonant, after this deletion of partials.

This portion of the experiment appears to argue against Helmholtz, that is, against acoustic dissonance as a basis for harmonic effects.

III-6. Cadence With Equally Spaced Partials

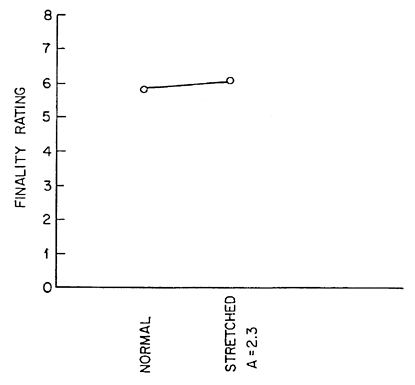
Figure 7 shows that this chord pair is given a relatively high finality rating. Furthermore, this rating, as we would expect, is not diminished by stretching (A = 2.3) the material. Thus, if one makes strong enough interactions between overtones, an impression of finality can be conveyed by a transition to an acoustically consonant situation. This would argue for Helmholtz's tonal consonance view of harmony.

IV. Supplementary Observations and Material

It is our observation that melodies are easily recognized despite stretching. A stretched (A = 2.4) version of the round, "Are You Sleeping, Brother John," was instantly recognized by an audience. The melody of harmonized stretched (A = 2.4) versions of "The Coventry Carol" and "Old Hundred" were recognized, but these had also been played unstretched.

In the harmonized stretched "Old Hundred" it seemed difficult to distinguish the inner voices. In fact, in single tones stretched A = 2.4, one tended to hear the partials as separated sounds rather than as fused into a tone of a single pitch. We believe that such fusion depends in part on the phenomenon of residue or periodicity pitch. ⁷ This has been noted by Cohen. ¹¹ She has observed further that the degree of fusion of a stretched tone depends on the envelope of the tone, and is greatest for an exponentially decreasing amplitude which gives a "struck" quality. ¹²

We observe that stretched tones sounded singly tend to fall apart into a group of partials, but when a sequence of such tones is played as a known melody the tones are heard as the individual notes of the melody.

It appears that whether or not a collection of stretched partials is heard as a single tone can depend on both the time evolution of the partial amplitudes and on the context (melodic or otherwise) in which the tones are heard.

V. Summary and Conclusions

We found :

1. Subjects can identify keys of both stretched and unstretched materials in an XMXM_t test.
2. Stretching destroys the perception of finality of cadences.
3. Removing dissonant overtones does not change the perception of the finality of cadences.

Result (2) argues for either Rameau or brainwashing.

Result (3) argues somewhat for brainwashing. We are taught that resolution is going from dissonance to consonance and in going from the dominant seventh to the tonic we accept the cadence as correct and final even when the tonal dissonance has been removed. But, cadences went from the dominant to the tonic before the dominant seventh was used.

Nonetheless, by using tones with equally spaced partials, we can get a sense of finality by going from a tonally dissonant chord to a tonally consonant chord. This argues for Helmholtz-Plomp.

We may observe that traditional harmony as we know it is like language, a complex but learnable art that is very difficult to explain.

The fact that under stretching melody is more robust than harmony seems to us salient and important.

Acknowledgment

Fig.1. Scores of passages used for key sensing tests.

Fig.2. Cadence (dominant to tonic) and anticadence (tonic to dominant).

Fig. 3. Finality ratings of stretched and normal cadences and anticadences. With normal (unstretched) partials the cadence is judged as having a great deal of finality and the anticadence as having little finality. With stretched partials, the finalities are essentially equal.

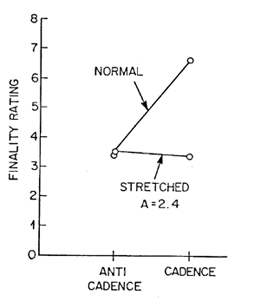
Fig. 4. Overtone frequencies of 7th cadence. The dots on the horizontal lines show the frequencies of the partials of a dominant seventh chord (above) and a tonic chord (bellow). The circles show deletions to make the minimum distance between partials a major second, and the crosses show additional deletions to make the minimum distance between partials a minor third.

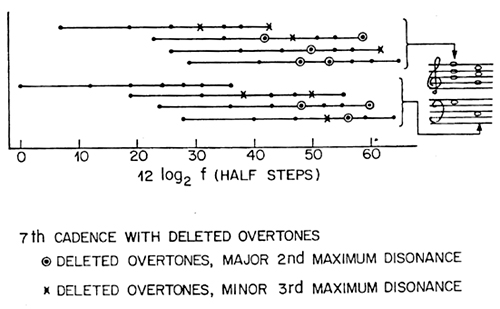
Fig. 5. Judgments of finality of cadence with partials deleted as in Fig.3 to remove tonal dissonance. For comparison, the square point is for a cadence stretched by A = 2.4.

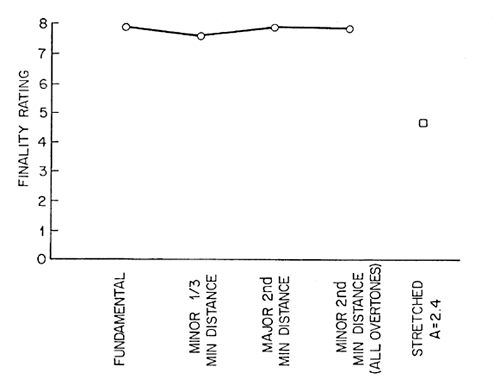
Fig. 6. A cadence with uniformly spaced overtones, going from a tonally dissonant to a tonally consonant chord.

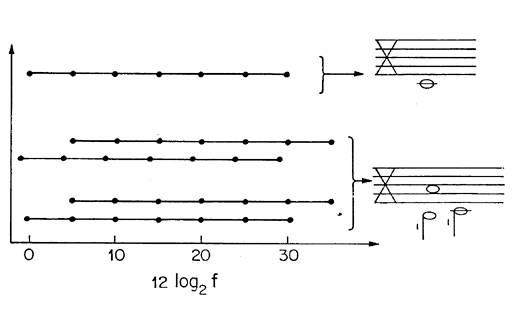
Fig. 7. Judgments of finality of the cadence of Fig. 6. It is judged as final with or without stretching.

1. M. V. Mathews, The Technology of Computer Music, (Cambridge, Mass.: The M.I.T. Press, 1969).
2. Frank H. Slaymaker, "Chords from Tones Having Stretched Partials," J. Acoust. Soc. Amer. 47, 1469-1571 (1970).
3. J. R. Pierce, "Attaining Consonance in Arbitrary Scales," J. Acoust. Soc. Amer. 40, 249 (1966).
4. H. Helmholtz, On the Sensations of Tone, (New York: Dover, 1954), Chap. 10.
5. R. Plomp and W. J. M. Levelt, "Tonal Consonance and Critical Bandwidth," J. Acoust. Soc Amer. 38, 548-560 (1965).
6. Jean-Philippe Rameau., Treatise on Harmony, (New York : Dover, 1971).
7. J. F. Schouten, "The Perception of Subjective Tones," K. ned. Akad. Wet. Proc. 41, 1086-1093 (1938).
8. Ernst Terhardt, "Pitch, Consonance and Harmony," J. Acoust. Soc. Amer. 55, 1061-1069 (1974).
9. Ernst Terhardt, Poster Demonstration, Rameau's "Basse Fundamentale," an Auditory Percept, "IRCAM Symposium sur la Psychoacoustique musicale," 11/13 July, 1977.
10. J. R. Pierce, Eight Tone Canon, Decca record DL 71080, "The Voice of the Computer."
11. Elizabeth Cohen, "Fusion and Consonance Relations for Tones with Inharmonic Partials," J. Acoust. Soc. Amer. 65, S123 (1970)(abstract).
12. Elizabeth Cohen, Ph.D. Thesis, Stanford University (1980).

____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .

____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .