
Tous droits réservés pour tous pays. All rights reserved.

 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
Philosophical Transactions of the Royal Society (vol 336), London Series B 1992
Copyright © Royal Society 1992
The trend toward using timbre in increasingly complex ways in music dates from orchestration practice in the last half of the 19th century ([Boulez, 1987]). This trend has been extended considerably with the advent of analog and digital means of sound generation and processing. These same means provide the researcher with the possibility to generate with precise control sounds of considerable complexity and thus to open the way to the systematic study of timbre perception.
For the psychologist, several interesting questions arise concerning a listener's ability to perceive and remember timbral relations in tone sequences ([Krumhansl, 1989]; [Mcadams, 1989]), as well as to build up hierarchical mental representations based these relations ([Lerdahl, 1987]). Research in the last 20 years (cf. [Plomp], 1970; [Risset & Wessel, 1982]; [Barrière, 1990]) has attempted to go beyond the loose negative definition of timbre given us by the field of psychoacoustics (i.e. timbre is what distinguishes two tones of identical pitch, loudness and perceived duration). To this end experimental paradigms that reveal the perceptual structure of timbral relations have been employed, and most notably those based on the multidimensional scaling of similarity (or dissimilarity) judgments.
In such a study, a number of tones differing in timbre (and equated for pitch, loudness, and perceived duration) are presented in all possible pairs to listeners who are asked to decide how dissimilar the tones of each pair are and to rate the dissimilarity on a scale of, say, 1 to 8. A multidimensional scaling algorithm is then applied to the matrix of judged dissimilarities. In many types of analyses, the algorithm tries to establish a monotonic relation between the dissimilarity ratings and Euclidean distances among the sounds arranged in a geometric structure in n dimensions, each sound being represented as a point. Sounds with similar timbres are thus near one another in the space and those with dissimilar timbres are farther apart. The experimenter tries solutions with varying numbers of dimensions and selects the solution that is a compromise between having a small difference between distances and ratings (which decreases with increasing n) and not having more dimensions than can be readily interpreted in terms of their underlying perceptual and/or psychophysical relevance to the group of listeners tested. Different studies on timbre have generally settled on two ([Plomb, 1970]; [Wessel, 1973, 1979]; [Ehresman & Wessel, 1978]; [Rasch & Plomp, 1982]) or three dimensions ([Grey, 1977]; [Krumhansl, 1989]). We will focus on the studies that adopted a three-dimensional solution.
Grey (1977) use 16 digitally recorded, analysed and resynthesized musical instrument tones performing an Eb3 (F0 = 311 Hz). Krumhansl (1989) used 21 synthetic tones developed by [Wessel, Bristow & Settel (1987)] on a Yamaha frequency modulation synthesizer: some of these tones were imitations of traditional Western orchestral instruments while others were hybrids (e.g. vibrone is a hybrid of vibraphone and trombone, and guitarnet is a hybrid of guitar and clarinet). Both Grey's and Krumhansl's spaces are qualitatively similar in the interpretation of their underlying dimensions, so we will confine our discussion to the latter since these tones were employed in our experiment.
A nonquantitative comparison of acoustic characteristics of the tones with their position along the various perceptual axes gave rise to the following interpretation (see Fig. 1). Dimension I seems related to the temporal envelope (rapidity of the attack and and degree of synchrony in the onsets of the harmonics) and might be called "attack quality". Sharp or biting attacks, such as that of the harpsichord, are found at one end of the dimension and softer, gentler attacks as with the clarinet are found at the other end. Dimension II seems related to a combined spectro-temporal property called "spectral flux". Instruments whose spectral envelope evolves relatively little over the duration of the tone (like the oboe) have low spectral flux compared to those whose spectrum changes a great deal (usually brightness increasing and decreasing with intensity as in the brass instruments). Dimension III seems related to the global spectral envelope and is called "brightness". [Grey & Gordon (1978)] have shown brightness to be highly correlated with the center of gravity of the long-term spectrum represented in terms of specific loudness and critical band rate ([Zwicker & Scharf, 1965]). Bright sounds (like the oboe) have a greater presence of energy in the higher harmonics than do duller sounds (like the French horn). In most cases the hybrid instruments were situated between the two instruments from which they were derived.
An additional aspect of the Krumhansl (1989) analysis (based on a technique developed by [Winsberg & Carroll, 1988])[1] revealed the existence of unique (though unspecified) perceptual features for certain instrument timbres. These features (called "specificities" in the analysis technique) are not taken into account by the three common dimensions. Examples of specific features might include the odd-harmonic, hollow tone colour of the clarinet which is not subsumed under brightness, or the "bump" at the return of the hopper on the end of a harpsichord tone. Eight of the 21 instruments had relatively high specificities (including the clarinet and harpsichord).
Figure 1. Timbre space derived from a three-dimensional scaling solution for dissimilarity judgments on 21 synthetic instrument tones. BSN = bassoon, CAN = cor anglais, CNT = clarinet, GTN = guitarnet (GTR/CNT), GTR = guitar, HCD = harpsichord, HRN = French horn, HRP = harp, OBC = obochord (OBO/HCD), OBO = oboe, OLS = oboleste (OBO/celeste), PNO = piano, POB = bowed piano, SNO = striano (STG/PNO), SPO = sampled piano, STG = string, TBN = trombone, TPR = trumpar (TPT/GTR), TPT = trumpet, VBN = vibrone (VBS/TBN), VBS = vibraphone. [Adapted from Krumhansl (1989)]
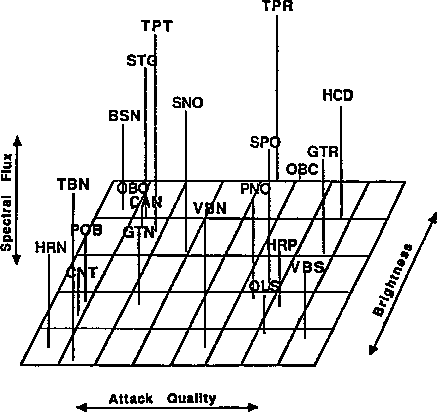
[Figure 1]
Once such a space has been quantified, one might ask whether the structure of the common dimensions is useful as a tool for predicting listeners' abilities to compare relations among the sounds. For example, can one use Euclidean spatial relations to define the properties of an interval formed by two timbres. This idea was initially developed by [Ehresman & Wessel (1978)] who applied [Rumelhart & Abrahamson's (1973)] parallelogram model of analogical reasoning in a semantic space to the timbre space composed of the tones used by Grey (1977). Rumelhart & Abrahamson took as a point of departure a three-dimensional space obtained by MDS techniques applied to dissimilarity judgments on animal names ([Henley, 1969]). They were interested in whether the structure of the space would allow them to predict people's choices when presented with an analogy task of the form A is to B as C is to D (or A:B::C:D). In general, if the relation between two objects, A and B, is represented as a vector in the space, the model predicts that subjects will chose an object D which is the closest to the end point of a vector starting at C and having the same magnitude and direction as AB (vectors are denoted in boldfaced type). They called this the ideal solution point, I. AB and CI thus form a parallelogram in the space. In their experiment, subjects were presented with analogies of the form A:B::C:{D1, D2, D3, D4}, where the Di's varied according to their distance from I. The probability of choosing Di as the best solution was found to be a monotonically decreasing function of the absolute distance of Di from I, thus supporting the parallelogram model. Ehresman & Wessel proceeded in analogous fashion with musical instrument tones. The underlying assumption behind the definition of a timbre interval as a vector is that processes exist for the encoding and processing of relations between timbres that are isomorphic with those for representing and processing vector quantities. While the results were not as strongly supportive of the parallelogram model as in the Rumelhart & Abrahamson study, they were better predicted by this model than a number of other models. This early paper is encouraging since it 1) formalizes the notion of a timbre interval as being composed of both distance and degree of change along important perceptual dimensions, and 2) shows that this definition is correlated with listeners judgments across intervals. The weakness of the study is that timbral vectors were computed from only a two-dimensional solution and that only relative vector magnitude was tested, ignoring the direction components. Our study systematically selected pairs of timbre vectors to be compared in an analogy task in order to test both magnitude and direction components.
Tones were derived from the set of 21 synthetic instruments described above. Each tone was realized playing an Eb3 at mezzo forte (MIDI velocity 70) on a Yamaha TX802 FM Tone Generator. All sounds had been equalized for pitch and loudness by Krumhansl (1989). There were some significant differences in duration, however, certain plucked and struck sounds lasting longer than sounds imitating forced vibration instruments (winds and bowed strings). The nominal duration for each tone was 300 ms.
The magnitude and direction components of a vector between any pair of sounds in the three-dimensional perceptual space derived by Krumhansl for these tones can be computed as follows (e.g. for A and B):
Magnitude (corresponds to the estimated perceived dissimilarity):
|AB| = {  (xAk - xBk)2 }1/2 , where xAk
is the coordinate on the kth dimension for timbre A;
(xAk - xBk)2 }1/2 , where xAk
is the coordinate on the kth dimension for timbre A;
Direction angles,  (degree of change on Dimension I) and
(degree of change on Dimension I) and
 (degree of change on Dimension II; the angle for Dimension III is
complementary to these two by the relation cos2
(degree of change on Dimension II; the angle for Dimension III is
complementary to these two by the relation cos2 +
cos2
+
cos2 + cos2
+ cos2
 1):
1):
 AB = cos-1 ((xA1-xB1)/|AB|),
AB = cos-1 ((xA1-xB1)/|AB|),
 AB = cos-1 ((xA2-xB2)/|AB|).
AB = cos-1 ((xA2-xB2)/|AB|).
Vectors can then be compared in terms of d,  , and
, and  .
Accordingly, four classes of four-tone sequences were constructed to be of the
form A:B::C:Di. Constraints were established for the selection of four
different kinds of Di, such that the magnitude and direction components of
AB and CDi were similar or quite different. These constraints are
schematically illustrated (for the two-dimensional case only) in Figure 2. They
can be formalized as follows :
.
Accordingly, four classes of four-tone sequences were constructed to be of the
form A:B::C:Di. Constraints were established for the selection of four
different kinds of Di, such that the magnitude and direction components of
AB and CDi were similar or quite different. These constraints are
schematically illustrated (for the two-dimensional case only) in Figure 2. They
can be formalized as follows :
Sequence 1--A:B::C:D1 (right magnitude, right direction on CD
with respect to AB); D1 close to I with small error ( ) on d,
) on d,
 , and
, and  :
:
|CD1| = |AB| +/-  d ,
d ,
 CD1 =
CD1 =  AB +/-
AB +/- 
 ,
,
 CD1 =
CD1 =  AB +/-
AB +/- 
 .
.
Sequence 2--A:B::C:D2 (right magnitude, wrong direction);
small error on d, but at least one of  CD2 or
CD2 or  CD2
must differ by at least 90º from
CD2
must differ by at least 90º from  AB or
AB or  AB,
respectively:
AB,
respectively:
|CD2| = |AB| +/-  d ,
d ,
|  CD2 -
CD2 -  AB | >= 90º and/or |
AB | >= 90º and/or |
 CD2 -
CD2 -  AB | >= 90º.
AB | >= 90º.
Sequence 3--A:B::C:D3 (wrong magnitude, right direction)
small error on  and
and  , but dCD3 must be larger than
dAB:
, but dCD3 must be larger than
dAB:
|CD3| >= 1.8 |AB|,
 CD3 =
CD3 =  AB +/-
AB +/- 
 ,
,
 CD3 =
CD3 =  AB +/-
AB +/- 
 .
.
Sequence 4--A:B::C:D4 (wrong magnitude, wrong direction):
|CD4| >= 1.8 |AB|,
|  CD4 -
CD4 -  AB | >= 90º and/or |
AB | >= 90º and/or |
 CD2 -
CD2 -  AB | >= 90º.
AB | >= 90º.
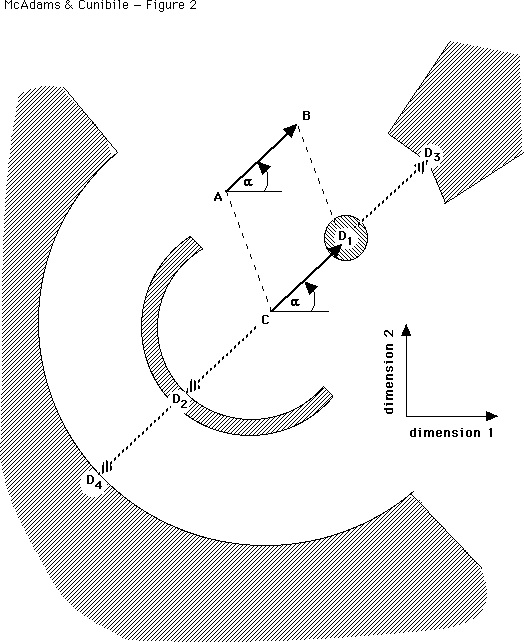
Figure 2. Two-dimensional representation of the different sequence
types. The angle  is with respect to dimension 1. The angle
is with respect to dimension 1. The angle  would be with respect to dimension 2 if the vectors were three-dimensional and
coming out of the page. The hashed areas represent the constraint space for the
end points of CDi vectors and are labeled D1, D2, D3 or D4, accordingly.
The ideal point I would be at the tip of the arrow-head for CD1. For the
three-dimensional case, the area would be a sphere for D1, a shell for D2, part
of a cone for D3, and a solid with a spherical hollow for D4.
would be with respect to dimension 2 if the vectors were three-dimensional and
coming out of the page. The hashed areas represent the constraint space for the
end points of CDi vectors and are labeled D1, D2, D3 or D4, accordingly.
The ideal point I would be at the tip of the arrow-head for CD1. For the
three-dimensional case, the area would be a sphere for D1, a shell for D2, part
of a cone for D3, and a solid with a spherical hollow for D4.
In the above equations, the maximum allowed value of the error terms was fixed
as follows: | d| <= 0.35, |
d| <= 0.35, |
 | <= 22.9º,
|
| <= 22.9º,
|
 | <= 22.9º. These values were determined empirically
to be as small as possible while giving a reasonable number of sequences for
each type listed above[2]. The range of d for timbre pairs used in the
experiment was 2.5-14.6 with a mean of 7.60. The range of angles was
14.2º-177.7º (mean = 95.7º) for
| <= 22.9º. These values were determined empirically
to be as small as possible while giving a reasonable number of sequences for
each type listed above[2]. The range of d for timbre pairs used in the
experiment was 2.5-14.6 with a mean of 7.60. The range of angles was
14.2º-177.7º (mean = 95.7º) for  and 7.7º-164.6º (mean
104.8º) for
and 7.7º-164.6º (mean
104.8º) for  .
.
Ideally, we want to find appropriate D1, D2, D3, and D4 for any given set of A, B, and C tones and ask listeners to rank order them with respect to their relative success in fulfilling the analogy as was done in Ehresman & Wessel (1978). This would allow us to test directly for the relative importance of magnitude and direction components of the timbral vectors. With the given space however, this was impossible since sets of 7 timbres (A, B, C, D1, D2, D3, D4) satisfying the constraints could not be found. We were obliged to settle on an experimental paradigm in which pairs of sequences were presented and subjects were to compare them and determine which best satisfied the analogy A:B::C:D. This reduced the stimulus search constraints to finding sets of five timbres (A, B, C, D, D'). The comparison types and the effect each is designed to test are listed in Table I. The following is an example of a D1/D4 comparison, where oboleste is a hybrid of oboe and celeste:
D1 - harp is to harpsichord as oboleste is to guitar, or
D4 - harp is to harpsichord as oboleste is to clarinet.
At least five versions of each of the six possible pairs of sequence types were found with the exception of A:B::C:D2/A:B::C:D3 (subsequently referred to simply as D2/D3). This comparison was thus dropped from the experiment. Each version of a comparison was composed of different timbres while still satisfying the stimulus constraints for the two sequence types. The use of multiple versions allows us to test the generality of the analogy task across different sets of timbres.
| Comparison Type | Vector Component Tested | Origin of Effect |
|---|---|---|
| D1/D2 | direction | right magnitude in both cases right direction on D1 wrong direction on D2 |
| D1/D3 | magnitude | right direction in both cases right magnitude on D1 wrong magnitude on D3 |
| D1/D4 | magnitude and direction | right magnitude and direction on D1 wrong magnitude and direction on D4 |
| D2/D3 | magnitude vs. direction | right magnitude and wrong direction on D2 wrong magnitude and right direction on D3 |
| D2/D4 | magnitude under wrong direction | wrong direction in both cases right magnitude on D2 wrong magnitude on D4 |
| D3/D4 | direction under wrong magnitude | wrong magnitude in both cases right direction on D3 wrong direction on D4 |
In each trial, listeners heard two sequences of four timbres with the following time structure, where the durations indicate silent intervals between the 300 ms tones: A - 500 ms - B - 900 ms - C - 500 ms - D - 1300 ms - A - 500 ms - B - 900 ms - C - 500 ms - D'. After a pause of 2700 ms, the 8-tone sequence was repeated once.
A complete block of 50 trials included the five sequence comparison types (D1/D2, D1/D3, D1/D4, D2/D4, D3/D4) each being presented in five versions with different timbres and with the order of presentation of the sequences counterbalanced.
Two groups of subjects were tested: 18 psychology students from René Descartes University without any formal musical training (nonmusicians) and 7 professional composers participating in a workshop on computer music at IRCAM. The nonmusicians were tested individually over headphones in a single-walled soundproof chamber and entered their responses on the computer keyboard. The composers were tested in a group listening to loudspeakers in a sound treated studio and entered their responses on a numbered answer sheet. The nonmusicians completed two blocks of trials while the composers completed a single block. The sounds were presented at a comfortable listening level.
Subjects were given an instruction sheet that explained the analogy task using a semantic and a visual example. The correct solutions to each example were explained. Six practice trials were given with a randomly selected set of experimental trials. No feedback was given on either the practice or the experimental trials. After completing the practice trials, any further questions the subject had were answered before proceeding to the first block of trials.
1. Subjects will prefer D1 over D2, D3, and D4 as a solution to the analogy, since it is the best fit to the parallelogram model. A corollary to this hypothesis would predict that the preference of D1 over D4 be stronger than that over D2 or D3 since D4 is the farthest removed in all respects from the ideal point.
2. D2 will be preferred over D4: listeners prefer the right magnitude even though the direction is wrong in both CD intervals.
3. D3 will be preferred over D4: listeners prefer the right direction even though the magnitude is wrong in both CD intervals.
4. There will be no differences among the different versions of each comparison type since the analogy judgment is based on a perception of abstract relations among the timbres of the stimulus tones.
5. The effects of Hypotheses 1-3 will be stronger for composers than for nonmusicians since the activity of reasoning with sound and making timbre judgments in composition will allow the former group to develop more consistent judgment strategies.
An additional point of interest concerns the missing D2/D3 condition. In the absence of this condition, a comparison between D1/D2 and D1/D3 preferences will indicate something of the relative effect of distance and direction. We have no a priori hypothesis about this result based on the parallelogram model.
The data consisted of percent choices of one of the paired sequences over the other for each version of each comparison type collected across order of presentation. An effect of block of trials (nonmusicians only) was only found for the D1/D2 comparison, the percent choice of D1 being greater in the second block (two-tailed, t(17) = 3.01, p < .01). In the subsequent analyses, the data are grouped across blocks for the nonmusicians.
The means for the experimental conditions are highly correlated between subject groups (r = .65, p < .01). While composers tend to express stronger preferences (one-tailed, t(24) = 1.66, p = .055), the patterns of both data sets are qualitatively similar. Thus Hypothesis 5 is at most only weakly supported by the data.
The means for each comparison type obtained for each subject group are shown in Figure 3. In order to test for differences from chance choice (50%), one-group t-tests were performed on means for each comparison type across versions for each of the subject groups. The Bonferoni-adjusted criterion was .005 (10 tests). All means except for the D3/D4 comparison were significantly different from chance for nonmusicians, and all except for the D1/D4 comparison were different from chance for composers.
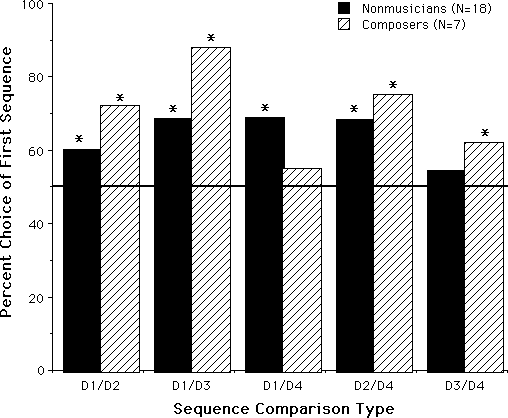
Figure 3. Global means (across versions, presentation orders, and listeners) for five sequence comparison types. The comparison type is labeled on the horizontal axis. The two groups of subjects (nonmusicians and composers) are shown are shown with solid and hashed bars, respectively. The horizontal line is positioned at 50% (chance choice). The asterisks over certain bars indicate that the mean is significantly different from chance.
Hypothesis 1 which predicted that D1 would be preferred over all other sequences is confirmed in all cases for nonmusicians and in all cases except D1/D4 for composers. This latter result is quite surprising, since according to the parallelogram model, D4 should be the farthest from the ideal point and D1 the closest. Examination of the means for the five versions of D1/D4 for composers shows that three hover around chance, one is significantly higher than chance (preference for D1), and one is quite lower than 50% (preference for D4) though this latter mean just misses being significantly different from 50%. In general, however, the results suggest that the parallelogram captures a significant portion of subjects' judgment strategies since the timbre closest to the ideal point is preferred over other more distant timbres. The corollary to Hypothesis 1 is not confirmed, i.e. preferences for D1 over D4 are not higher than those of D1 over D2 or D3. This will require further reflection since the parallelogram model of Rumelhart & Abrahamson (1973) predicts monotonically decreasing preference with increasing distance from the ideal point.
That relative distance between timbre pairs can be evaluated even though the directions are dissimilar is suggested by the fact that the mean preference for D2 is reliably above chance for both subject groups. Hypothesis 2 is thus confirmed indicating that the distance component of the timbral change is perceptually important in perceiving timbral relations.
Hypothesis 3 (D3 is preferred over D4) is confirmed for composers but not for nonmusicians. This result suggests that the latter group can evaluate relative direction of timbral change even though the distances between the timbres are quite different. Examination of the five versions of D3/D4 for the nonmusicians reveals that two had means reliably above 50% (preference for D3) and one was significantly below 50% (preference for D4).
In the absence of a D2/D3 condition, a comparison of D1/D2 means with those for D1/D3 suggests that distance change across timbre pairs (D1/D3) is more easily noticed than direction change (D1/D2), since D1 is preferred more over D3 than over D2. This difference is not statistically significant, however.
Overall the results are encouraging, indicating an ability to make judgments on timbral relations. However, some of these global effects need to be qualified by a closer look at the different versions grouped under each comparison type.
To test for effects of individual versions within comparison type, one-way analyses of variance with repeated measures on version were performed. The results are shown in Table II. For both subject groups, four out of five comparison types have significant overall differences between versions. This indicates that not every version of each comparison had the same perceptual result and was thus not judged in a similar way. In particular, one notes a great dispersion of means for certain comparisons (D3/D4 for nonmusicians and D1/D4 for composers) that result in the global mean being not different from random choice. Globally, we must reject Hypothesis 4 which predicted equal performance for all versions of a comparison type.
| Nonmusicians | Composers | |||
|---|---|---|---|---|
| Comparison Type | F(4, 68) | p | F(4, 24) | p |
| D1/D2 | 3.58 | < .01 | 8.26 | < .005 |
| D1/D3 | 2.36 | > .05 | 3.12 | > .10 |
| D1/D4 | 4.49 | < .005 | 5.14 | < .005 |
| D2/D4 | 9.20 | < .001 | 7.10 | < .001 |
| D3/D4 | 9.00 | < .001 | 3.88 | < .05 |
(c) Effect of the relative distance of Di's from the ideal point
According to the Rumelhart & Abrahamson model, the choice of one sequence over another should be a monotonically increasing function of the distance between the ideal point and D. Therefore, for each comparison type, these distances were calculated and the mean percent choices for each comparison type were regressed onto the difference between these distances. This analysis indicates the degree to which judgments may have been based purely on the relative distance of D from I in each sequence. The regression was performed independently for nonmusician and composer groups. For nonmusicians the regression yielded a significant fit between mean data and distances (R = .48; F(1,23) = 6.80, p < .05). While the fit is not bad, the regression only accounts for 23% of the variance in the data indicating that other factors are entering into the judgments that are unaccounted for by a simple distance-from-ideal-point model. For composers, the fit between mean data and distances is not significant (R = .04; F(1,23) = 0.04). In spite of the strong correlation between the means for nonmusicians and composers, there appears to be no relation between relative distance from the ideal point and the sequence preferred as best completing the analogy for the composers.
Another possibility is that listeners made judgments based on the relative degree of change along the different perceptual dimensions. Accordingly, we performed a multiple regression of the differences in change along each dimension between AB and CD or CD' vectors onto mean percent choice for each group. For nonmusicians, the fit was not significant (R = .46; F(3,21) = 1.93) whereas for composers the fit was significant (R = .57; F(3,21) = 3.33, p < .05). The partial F's for the multiple regression show that differences in change along Dimensions I and II (attack, spectral flux) are largely responsible for this fit. Taken together, these two regression analyses may indicate differences in listening and judgment strategies between the two groups.
A number of experimental conditions were designed within the framework of a Euclidean distance model of timbre space (Krumhansl, 1989) in order to test listeners abilities to perceive timbral relations and to judge their similarity in terms of magnitude and direction of timbre change. These results support and extend those of Ehresman & Wessel (1978).
A vector model of timbre intervals was fairly successful at predicting the choice of one type of sequence over another, where the sequences varied in the degree to which the magnitude and direction components of the timbral vectors matched across pairs of timbres. In general, timbres close to the ideal point predicted by the vector model are preferred as best fulfilling an analogy of the form A:B::C:D than are timbres that are at some distance from that point (conditions D1/D2, D1/D3, D1/D4). We have also shown that in some cases the model even predicts preference when both D's in a sequence comparison are quite far removed from I, indicating an ability to appreciate the appropriate vector magnitude under conditions of wrong direction (D2/D4) and of appropriate direction under conditions of wrong magnitude (D3/D4), though the latter condition is quite weak. What the model does not do is make predictions on the relative contributions of magnitude and direction of the comparison timbre vector. This is a subject for future research.
The strong effect of the timbre set chosen to realize each comparison type suggests a relative lack of generalizability of timbral interval perception across different timbres. This result may be due to a number of factors that were not controlled in this study: 1) there may be a relative instability of judgment strategies, since most of the listeners have never encountered a listening situation in which focussing on, or comprehending, abstract timbral relations was appropriate; 2) there may be effects of the relative magnitude of a given vector and the distance between to-be-compared vectors: very large vectors may be difficult to compare with precision and small vectors that are very far apart in the space may also be difficult to compare; 3) there may be effects of the degree of change along different common dimensions: the perceptual weights of change along individual dimensions may not be equivalent in this kind of listening task; and 4) there may be effects of specific features of individual timbres that are not taken into account by the common dimensions of the timbre space, but which influence the perceived distances between timbres and thus the timbre intervals that are to be compared.
Portions of this study were realized in partial fulfillment of the requirements for J.-C. Cunibile's Master's thesis at the Laboratoire de Psychologie Expérimentale, Université René Descartes ([Cunibile, 1991]).
 (xik -
xjk)2 + si + sj}1/2, where xik is the coordinate on the
kth dimension for tone i and si is the estimated specificity for
tone i that is not accounted for by the common dimensions.
(xik -
xjk)2 + si + sj}1/2, where xik is the coordinate on the
kth dimension for tone i and si is the estimated specificity for
tone i that is not accounted for by the common dimensions.
 and
and 
 leads in some cases to an
leads in some cases to an

 as large as 86º which results in the D for that
sequence being farther removed from I. The mean |
as large as 86º which results in the D for that
sequence being farther removed from I. The mean |
 | in D1
and D3 sequences was 36.3º with a standard deviation of 22.6º.
| in D1
and D3 sequences was 36.3º with a standard deviation of 22.6º.
Grey, J. M. (1977) Multidimensional perceptual scaling of musical timbre. Journal of the Acoustical Society of America, 61, 1270-1277.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .