
Tous droits réservés pour tous pays. All rights reserved.

 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
Stephen McAdams
1
R. Llinas & P. Churchland (eds.), The Mind-Brain Continuum, pp. 251-279, MIT Press, Cambridge, MA. 1996
Copyright © MIT Press 1996
One of the main goals of auditory cognitive psychology is to understand how humans can "think in sound" outside the verbal domain (McAdams and Bigand, 1993). Within the field of contemporary auditory cognition research, music psychology has a very important status. This field in its current form situates itself strongly within the cognitive framework in the sense that it postulates internal (or mental) representations of abstract and specific properties of the musical sound environment, as well as processes that operate on these representations. For example, sensory information related to frequency is transformed into pitch, is then categorized into a note value in a musical scale and then ultimately is transformed into a musical function within a given context. Some research has begun to address how these computations can be implemented, focusing on the nature of the input and output representations as well as on the algorithms used for their transformation. A still smaller number of researchers have begun studying the way in which these representations and algorithms are instantiated biologically in the human brain (Marín, 1982; Zatorre, 1989; Peretz, 1993). The goal of this chapter is to present research that lays the functional base for more neuropsychologically oriented work.
The processing of musical information may be conceived globally as involving a number of different "stages" (Fig. 1) (McAdams, 1987; Bigand, 1993a; Botte et al., 1995). Following the spectral analysis and transduction of acoustic vibrations in the auditory nerve, the auditory system appears to employ a number of mechanisms (primitive auditory grouping processes) that organize the acoustic mixture arriving at the ears into mental "descriptions" (Bregman, this volume). These descriptions represent events produced by sound sources and their behavior through time. Research has shown that the building of these descriptions is based on a limited number of acoustic cues that may reinforce one another or give conflicting evidence. This state of affairs suggests the existence of some kind of process (grouping decisions) that sorts out all of the available information and arrives at a representation of the events and sound sources that are present in the environment that is as unambiguous as possible. According to Bregman's (1990) theory of auditory scene analysis, the computation of perceptual attributes of events and event sequences depends on how the acoustic information has been organized at an earlier stage. Attributes of individual musical events include pitch, loudness, and timbre, while those of musical event sequences include melodic contour, pitch intervals, and rhythmic pattern. Thus a composer's control of auditory organization by a judicious arrangement of notes can affect the perceptual result.
Once the information is organized into events and event streams, complete with their derived perceptual attributes, what is conventionally considered to be music perception begins. The auditory attributes activate abstract knowledge structures that represent in long-term memory the relations between events that have been encountered repeatedly through experience in a given cultural environment. That is, they encode various kinds of regularities experienced in the world. Bregman (1993) has described regularities in the physical world and believes that their processing at the level of primitive auditory organization is probably to a large extent innate. There are, however, different kinds of relations that can be perceived among events: at the level of pitches, durations, timbres, and so on. These structures would therefore include knowledge of systems of pitch relations (such as scales and harmonies), temporal relations (such as rhythm and meter), and perhaps even timbre relations (derived from the kinds of instruments usually encountered, as well as their combinations). The sound structures to be found in various occidental cultures are not the same as those found in Korea, Central Africa or Indonesia, for example. Many of the relational systems have been shown to be hierarchical in nature and I will return to this point later.
Figure 1 . Schema illustrating the various aspects of musical information processing.
So the raw perceptual properties associated with musical events and groups of events activate the structures that have been acquired through acculturation, and the events thus acquire functional significance and evoke an interpretive framework (the key of F# major and a waltz meter, for example). A further stage of processing (event structure processing) assembles the events into a structured mental representation of the musical form as understood up to that point by the listener (McAdams, 1989). Particularly in Western tonal/metric music, hierarchical organization plays a strong role in the accumulation of a mental representation of musical form. At this point there is a strong convergence of rhythmic-metric and pitch structures in the elaboration of an event hierarchy in which certain events are perceived to be stronger, more important structurally, and more stable. The functional values that events and groups of events acquire within an event hierarchy generate perceptions of musical tension and relaxation or, in other words, musical movement. They also generate expectancies about where the music should be going in the near future based both on what has already happened and on abstract knowledge of habitual musical forms of the culture--even for pieces that one has never heard before. In a sense, we are oriented--by what has been heard and by what we "know" about the musical style--to expect a certain type of event to follow at certain pitches and at certain points in time (Dowling et al., 1987).
The expectancies drive and influence the activation of knowledge structures that affect the way we interpret subsequent sensory information. For example, we start to hear a certain number of pitches, a system of relations is evoked and we infer a certain key; we then expect that future information that comes in is going to conform to that key. A kind of loop of activity is set up, slowly building a mental representation that is limited in its detail by how much knowledge one actually has of the music being heard. It is also limited by one's ability to represent things over the long term, which itself depends on the kind of acculturation and training one has had. It does not seem too extreme to imagine that a Western musician could build up a mental structure of much larger scale and greater detail when listening to a Mahler symphony that lasts one and half hours, than could a person who just walked out of the bush in Central Africa. The reverse would be true for the perception of complex Pygmy polyphonic forms. However, on the one hand we are capable of hearing and enjoying something new, suggesting that there may be inborn precursors to musical comprehension in all human beings that makes this possible. On the other hand, what we do hear and understand the first time we encounter a new musical culture is most likely not what a native of that culture experiences.
The expectancies generated by this accumulating representation can also affect the grouping decisions at the basic level of auditory information processing. This is very important because in music composition, by playing around with some of these processes, one can set up perceptual contexts that affect the way the listener will tend to organize new sensory information. This process involves what Bregman (1990) has called schema-driven processes of auditory organization. Finally, there is some evidence now that attentional processes can affect the way information is processed in the auditory periphery by way of the efferent projections innervating the outer hair cells in the cochlea (Puel et al., 1988; Giard et al., in press), though their role in everyday perception is not yet clear. While the nature and organization of these stages are probably similar across cultures in terms of the underlying perceptual and cognitive processing mechanisms involved, the "higher level" processes beyond computation of perceptual attributes depend quite strongly on experience and accumulated knowledge that is necessarily culture-specific.
Let us now take a closer look at each of these areas. I cannot possibly do justice to the vast amount of research that has been conducted in music psychology in the last 25 years or so within the space of this chapter. I can only present a very brief overview of a few selected topics to demonstrate how it is possible to do rigorous experimental research on such an ephemeral beast as musical experience. The majority of the material will focus on the more specifically musical areas of abstract knowledge structures and event structure processing.
So on the one hand, abstract knowledge structures comprise systems of relations between musical categories that form the basis upon which the musical syntax of a given culture is developed (such as pitch categories, scale structures, and tonal and harmonic hierarchies). These systems imply the existence of psychological processes of categorization, abstraction and coding of relations among categories, as well as the functional hierarchization of these relations.
And on the other hand, learned generalizations from musical forms realized in time can comprise a lexicon of abstract patterns that are frequently encountered in a given culture (such as prototypical melodic forms, harmonic progressions, or formal schemes of musical structure like Western sonata form or Indian rg form). A pattern lexicon would imply the abstraction and coding of structures that underly the "surface" of heard events. The main difference between abstract systems of relations between musical categories (like scales and tonal hierarchies) and a lexicon of abstract patterns (like formal musical schemas) is that the former are a sort of hierarchical alphabet "out of time", from which elements can be drawn to build musical materials, while the latter are sequential schemes that can be elaborated with these constituent elements.
In what follows I will focus primarily on systems of pitch relations in Western tonal music. All humans perceive a large continuum of pitch (Fig. 2, level 1). However, the pitch systems of all cultures consist of a limited set of pitch categories that are collected into ordered subsets called scales. In the Western equal-tempered pitch system, all diatonic scales of seven notes (Fig. 2, level 3) are derived from an alphabet of the 12 chromatic notes within an octave (Fig. 2, level 2). The pitches of adjacent notes in the chromatic scale are separated by a semitone which corresponds to a frequency difference of approximately 6%. The octave is a special interval (a 2:1 frequency ratio) at which two pitches, though separated along the pitch dimension, seem to have something in common, or are perceived to be equivalent. In all cultures that name the pitches in scales, two pitches separated by an octave are given the same name (e.g. do re mi fa sol la ti do or C D E F G A B C in the Western system, and Sa Re Ga Ma Pa Dha Ni Sa in the Indian system). It has been shown that young infants (Demany and Armand, 1984) and white rats (Blackwell and Schlossberg, 1943) make errors in pitch discrimination for pitches separated by an octave, suggesting that octave equivalence may be a universal feature of the mammalian auditory nervous system.
Figure 2. Different levels of representation of musical pitch in Western tonal music (from top to bottom): spiral representing the psychophysical pitch continuum with octave equivalence; categorization of pitch continuum into the 12-note equal-tempered chromatic scale; selection of a diatonic 7-note scale from the chromatic scale; functional interpretation of certain notes as being more stable or perceptually important than others (context of C major in this case). [From Fig. 4.14, Dowling and Harwood (1986). (c) Academic Press. Adapted with permission.]
A given scale is defined by the pattern of intervals between the pitch categories. A major scale has the pattern 2--2--1--2--2--2--1 in numbers of semitones between scale steps (Fig. 3, upper panel). One type of minor scale (called natural minor) has the pattern 2--1--2--2--1--2--2 (Fig. 3, lower panel). Within a scale there often exists a functional hierarchy among the pitches (Fig. 2, level 4), as well as among chords that can be formed of the pitches. In the Western tonal pitch system, some pitches and chords, such as those related to the first and fifth degrees of the scale (C and G are the tonic and dominant notes of the key of C major, for example) are structurally more important than others (Fig. 3). This hierarchization gives rise to a sense of key. In fact when chords are generated by playing several pitches at once, the chord that is considered to be most stable within a key, and in a certain sense to "represent" the key, comprises the first, third and fifth degrees of the scale. In tonal music, one can establish a sense of key within a given major or minor scale and then move progressively to a new key (a process called modulation) by introducing notes from the new key and no longer playing those from the original key that are not present in the new key. Such phenomena suggest that there also exists a functional hierarchy among the keys that affects a listener's perception of tonal movement within a piece of music as well as his or her local interpretation of the function of given pitches and chords. Let's now look more closely at examples of research that have studied the nature of the mental structures underlying these music theoretic principles.
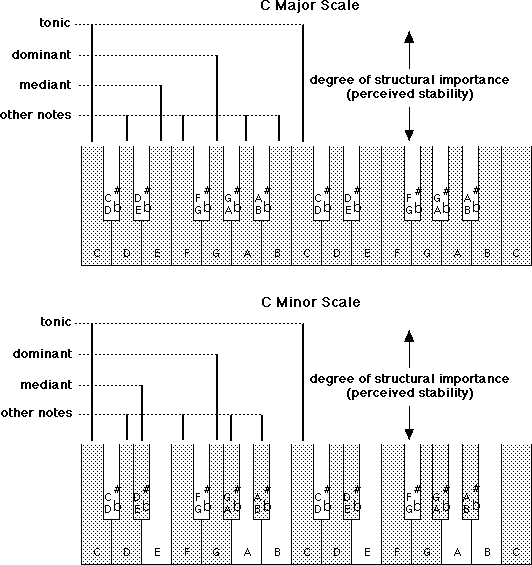
Figure 3. Piano keyboard representation of the scales of C major and C minor. Notes in each scale are shaded. The relative importance of the first (tonic - C), fifth (dominant - G) and third (mediant - E) degrees of the scale is illustrated by the length of the vertical bars. The other notes of the scale are more or less equally important followed by the chromatic notes that are not in the scale (unshaded).
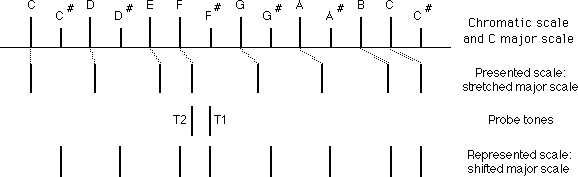
Figure 4. This diagram illustrates the chromatic scale from which the C major scale (longer vertical lines) is derived, the stretched major scale (starting on C and ending on C#) presented to listeners by Jordan and Shepard (1987), and the shifted major scale template thought to represent the framework against which listeners judged the fittingness of probe tones (positioned on C# major). Listeners judgments indicate that the fittingness of probe tones was judged with respect to a shifted major scale template rather than in relation to a perfect pitch memory of the stretched scale. For example, tone T1 (fourth note of the shifted scale) would be judged as well-fitted while T2 (fourth note of the stretched scale) would be judged as poorly fitted even though T2 was actually present in the context stimulus and T1 wasn't.
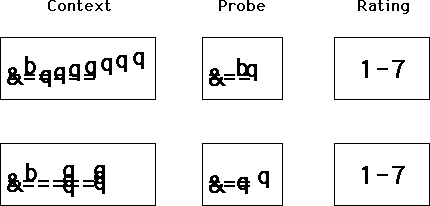
Figure 5. Schema of the probe-tone technique developed by Krumhansl (1979). A context-establishing stimulus is followed either by a probe tone that is rated for its fittingness with the context, or by a pair of events whose degree of relatedness is rated with respect to the context. Ratings are made on a numerical scale.
Krumhansl (1990, chap. 3) has shown that the hierarchy of tonal importance revealed by these profiles is strongly correlated with the frequency of occurrence of notes within a given tonality (the tonic appears more often than the fifth than the third, and so on). It also correlates with various measures of tonal consonance of notes with the tonic, as well as with statistical measures such as the mean duration given these notes in a piece of music (the tonic often having the longest duration). These correlations suggest that the acquisition and appreciation of a stable mental representation of the tonal hierarchy could be initially based on simple statistical and psychoacoustic properties of the musical surface. The importance of basic sensory qualities like dissonance (related to the psychoacoustic attribute roughness) should not be underestimated (Plomp and Levelt, 1965; Kameoka and Kuriyagawa, 1969). They form what Mathews et al. (1987) have called the "acoustic nucleus" from which higher level musical functions have evolved. While the higher level functions are specific to a given culture, they may have common origins, across cultures, in a given result of sensory processing.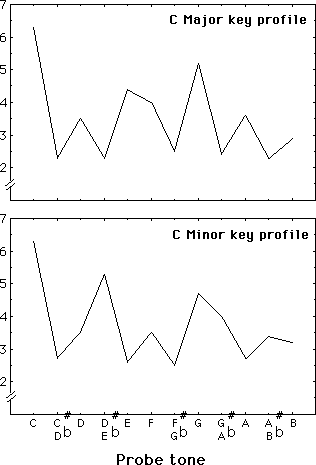
Figure 6 . Major and minor profiles derived with the probe-tone technique from fittingness ratings by musician listeners. [From Fig. 2, Krumhansl and Kessler (1982). (c) American Psychological Association. Adapted with permission.]
The establishment of a tonal context has a great deal of influence on the perception of relations between chords. If listeners are asked to rate the relatedness of two chords either independently of a context or within the context of two different keys, their relatedness varies as a function of the harmonic context (Bharucha and Krumhansl, 1983). In Figure 7, the relatedness judgments have been analyzed by a multidimensional scaling technique that positions each chord in a Euclidean space such that chords judged as being closely related are near one another and those judged as being less related are farther apart. Note that in the absence of a tonal context (that is within the context of random presentation of all the chord pairs), the chords C major and G major (I and V, respectively, on the left side of the middle panel), have a similar relation to that between the chords F# major and C# major (I and V, respectively, on the right side of the middle panel); in other words they are the same distance apart in this two-dimensional representation of the relatedness judgments. However, note that in the C major context, the I and V chords of C major are perceived as more closely related than are the I and V chords of F# major, while in the F# major context the reverse is true, in spite of the fact that acoustically the pairs of events were identical. This result suggests that relatedness depends on the harmonic context within which the chords are interpreted. These relations are considered to determine the harmonic expectancies that can be measured in listeners and also reflect the frequency of occurrence of chord progressions in tonal music.
Krumhansl (1990, chap. 7) has also demonstrated quite elegantly that the hierarchies for notes and chords can be used to predict listeners' mental representations of relations among keys. These relations would represent the next higher level in the hierarchical knowledge structure concerning the syntax of pitch relations in tonal music.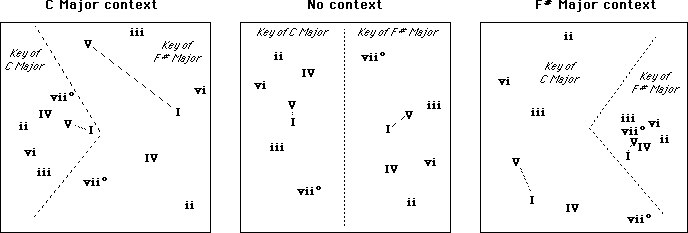
Figure 7. Effect of key context on perception of relatedness of chords. Note the changing distance between I and V chords in both keys as a function of context. These chords are closely related when they are the tonic and dominant chords of an established key but are distantly related when outside of the key. The Roman numerals indicate the degree of the scale on which the triad is based. Major chords are represented by upper case numerals, minor chords by lower case numerals and diminished chords by deg.. [From Fig. 1, Bharucha and Krumhansl (1983). (c) Elsevier Science Publications. Adapted with permission.]
A variant of this test was designed for two right-handed callosotomy (or split-brain) patients such that harmonic perception in each hemisphere could be tested independently (Tramo et al., 1990). Only the right hemisphere manifested the normal interaction between intonation detection accuracy and harmonic relatedness of prime and target chords. This result suggests that associative auditory functions which generate expectancies for harmonic progression in music are lateralized within the right hemisphere. Previous work by Zatorre (1989) has demonstrated elegantly that the processing of musical pitch also seems to be lateralized in the right hemisphere. Further work is required to determine how pitch computation and processes involved in the generation of harmonic expectancies interact computationally in the brain.
Until the middle of the 19th century, the role that timbre played in music was either one of carrying a melodic voice and allowing it to be distinguished from other voices, or one of signalling section boundaries by changes in instrumentation. It thus primarily had a role as an attribute according to which sound events could be grouped or segregated on the basis of their similarity. With the advent of the symphony orchestra, timbre became an object of musical development in its own right and composers began to build up composite timbres with sophisticated orchestration techniques (Boulez, 1987). Further on, in the latter half of the 20th century, first electronic and then digital sound synthesis techniques suddenly gave the musician undreamed-of control over this auditory attribute. Composers were no longer obliged to work with the "found objects" of the orchestra, but could begin to compose the sound from the inside. This opened the door to a structural use of timbre that in principle could come to rival that of pitch. However, there is no theory, nor even a common practice, in such uses of timbre and so many composers, while discovering the occasional stunning result by creative intuition, admit that they have no systematic approach to integrating timbre into a musical discourse.
The development in cognitive psychology of multidimensional scaling techniques has allowed us to begin to penetrate the nature of this multifarious attribute. Following from pioneering work by Grey (1977), Krumhansl (1989) has found that in dissimilarity judgments between timbres, musician listeners tend to base their judgments on about three main perceptual dimensions plus a number of distinctive features that belong to individual timbres (Fig. 8). We have recently succeeded in finding acoustic parameters that correlate very strongly with the position of the timbres along these dimensions (Krimphoff et al., 1994), which means we can now build sound synthesis devices that have powerful perceptual controls on them. The continuous dimensions include 1) the attack quality (horizontal axis) which distinguishes plucked and struck sounds from blown and bowed sounds and is correlated with the logarithm of the attack time, 2) brightness (depth axis) which distinguishes sounds containing a greater preponderance of high frequencies from those whose spectra are limited to lower frequencies and is correlated with the spectral center of gravity (amplitude-weighted mean frequency), and 3) the degree of variation in global spectral envelope among adjacent frequency components (vertical axis). We have yet to analyze acoustically the distinctive features that the analysis suggests exist for certain timbres, but they certainly involve acoustic characteristics that are not generally shared among the timbres tested. These features are what distinguishes most clearly sound sources from one another and may well be involved in what allows their recognition (McAdams, 1993). The common dimensions may be candidates for the development of musical structure, though their respective degrees of salience vary among classes of listeners (Donnadieu et al., 1994).
But more to the point about timbre as a structuring force in music, we have asked the following, related questions (McAdams and Cunibile, 1992): Can listeners perceive relations among timbres in a way that allows recognition of that relation itself when played with different timbres? And can these relations be derived from the timbre space described above? In more musical terms these questions translate as: Do listeners perceive timbre intervals in a way analogous to pitch intervals and can these intervals be defined with respect to timbre space? To investigate this we performed experiments using what one might call a timbre analogies task originally developed by Ehresman and Wessel (1978). We define a timbre interval as a vector between two points in the space (Fig. 9). The vector represents the degree of change along each underlying perceptual dimension and corresponds closely to the notion of pitch interval that has been shown to be so crucial to the mental representation of melody and harmony. For example, it is well established in music psychology that a melody (a pattern of pitch intervals) can be transposed (translated to a different starting pitch) and still be easily recognized if the interval pattern remains the same. Analogously for timbre, to find a similar interval starting from a different timbre in the space, one has simply to translate the vector, keeping the same length and orientation. In geometrical terms, this operation is equivalent to finding two other points that form a parallelogram with the two original points. Our results showed that both composers and nonmusician listeners can perform the task, though the musicians' judgments are generally more coherent with the timbral vector hypothesis than are those of nonmusicians. This study suggests that relations between timbres in this space can be perceived in their own right. Such developments may lead to a demonstration of the psychological plausibility of establishing timbre scales and melodies, and perhaps even of timbral hierarchies (Lerdahl, 1987). While this is only a preliminary study, that actually poses more questions than it answers since there is considerable variability among listeners, it opens the possibility that psychological research can give some useful conceptual tools to the practising composer.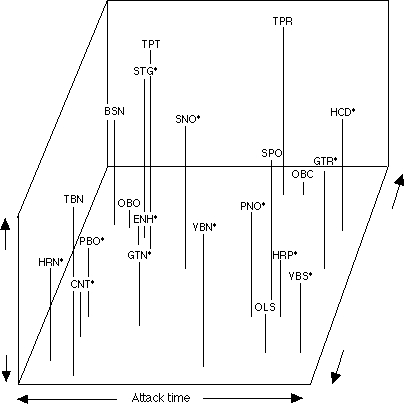
Figure 8. Three-dimensional timbre space derived from multidimensional scaling of dissimilarity judgments on 21 synthesized timbres by Krumhansl (1989). Axes are labelled with acoustical correlates to the perceptual dimensions analyzed by Krimphoff et al. (1994). Sounds with significant distinctive features not accounted for by their distance from other timbres in the three-dimensional space are marked with an asterisk. Abbreviations: HRN = French horn, TBN = trombone, CNT = clarinet, PBO = pianobow (bowed piano), BSN = bassoon, OBO = oboe, ENH = English horn, GTN = guitarnet (guitar/clarinet hybrid), STG = bowed string, TPT = trumpet, SNO = striano (bowed string/piano hybrid), VBN = vibrone (vibraphone/trombone hybrid), PNO = piano, OLS = oboleste (oboe/celeste hybrid), SPO = digitally sampled piano, HRP = harp, TPR = trumpar (trumpet/guitar hybrid), VBS = vibraphone, OBC = obochord (oboe/harpsichord hybrid), GTR = guitar, HCD = harpsichord.
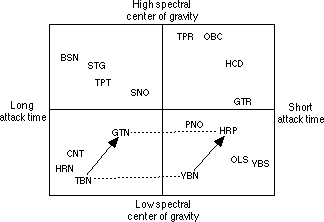
Figure 9. Timbral intervals may be conceived of as vectors in timbre space (shown as two-dimensional in this figure). The vectors represent the degree of change between two timbres along each salient perceptual dimension. The perception of an interval presupposes the brain's capacity to extract relational information from the sensory representation of the pair of timbres. An interval equivalent to TBN-GTN may be found starting from VBN by finding a point that best completes a parallelogram with the three other points: HRP in this case. (For abbreviations see Fig. 8.)
The first component parses the event stream into a grouping hierarchy. Groups of smaller time span are embedded in groups of longer time span recursively. In parallel, the second component analyzes the sequence into a hierarchical metric structure of alternating strong and weak beats that occur regularly in time. Strong beats at one level become beats at the next level. It is thus a reductional hierarchy in which weak beats are progressively reduced out. These two analyses converge to give a hierarchical segmentation of the event stream into time-spans. The third component assigns a reductional hierarchy of structural importance to the pitches in each time span as a function of their position in the segmentational structure. An important pitch at one level is carried upward to the next level, leaving behind the pitches that are subordinate to it. In this way the representation of melodic patterns is "reduced" to the pitches that have a structural importance, hence the label "time-span reduction" for this component. It should be noted that the level to which such a reduction can reasonably take place is probably limited by constraints on working memory, though this subjects has only recently begun to be studied in music psychology.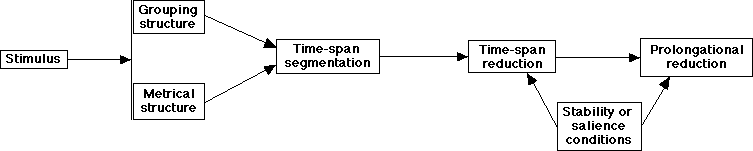
Figure 10. Major components of Lerdahl and Jackendoff's generative theory of tonal music.
Stability and salience conditions that play a role in determining structural importance are based on abstract musical knowledge represented in the form of tonal and harmonic hierarchies as discussed previously, or on psychoacoustic properties that make a given event stand out with respect to its neighbors. There is thus a convergence of pitch and rhythm information in the elaboration of the event hierarchy at this stage. Finally, the event hierarchy serves in the development of the last hierarchical representation, called prolongational reduction in the theory. This component expresses the melodic and harmonic tension and relaxation as well as the continuity and progression of the musical discourse. It is strongly based on the degree of relatedness of structurally important pitches and chords. Closely related chords produce a prolongation of the current state of tension or relaxation whereas more distantly related chords can progress to greater tension or greater relaxation. Let's now examine in more detail the experimental results related to each of these theoretical components.
One of the important musical by-products of grouping is the occurrence of subjective accents. These occur on isolated events, on the second of two events in a group, and on the first and last of a string of events (Povel, 1984).
Figure 11. Examples of temporal and qualitative segmentation according to the grouping rules of Lerdahl and Jackendoff (1983). In the temporal proximity rules, a change in duration of a note (rest) or of the time interval between note onsets (attack point) can provoke a segmentation. In the qualitative similarity rules, an abrupt change in pitch register, loudness, timbre or articulation (legato [long notes] vs staccato [short notes]) can also result in segmentation.
For a given sequence of events, listeners first extract a regular pulse at a certain tempo such that the majority of the perceived events fall on a beat rather than between the beats. Work by Fraisse (1963) and more recently by Drake and Botte (1993) has shown that a preferred tempo for the beat level exists at about 1.7 beats/sec (inter-onset time = 600 msec) or a musical tempo marking of 100/min, though for musicians the range can be larger extending from 100 to 900 msec. Next, on the basis of accents produced by the grouping structure, the listener tries to infer a metric structure in which every N beats is accented, where N is usually 2, 3 or 4. For example, in a waltz, it is relatively easy to extract the underlying pulse on the basis of the event sequence and then to determine that one out of every three is accented thus giving a ternary meter characteristic of the waltz. Povel (1984) has shown that if the accents resulting from the grouping structure are regularly spaced, a meter is easily inferred from a sequence, and the rhythmic pattern is also more easily remembered and reproduced (Fig. 13). When several possible beat structures can be fit to a given sequence, the sense of meter is more ambiguous and the pattern itself is more difficult to remember and reproduce. These results suggest that patterns that fit unambiguously to a given metric scheme have an internal representation that is more precise.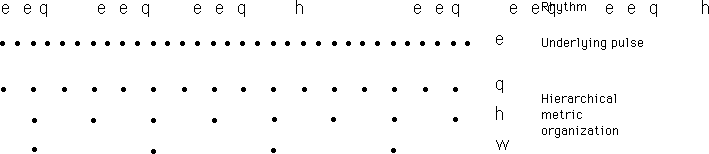
Figure 12. Metric organization of a rhythm pattern. An underlying pulse is determined from the smallest time interval of which the other intervals are integer multiples. For this rhythm, the lower metric levels are binary subdivisions of higher levels. The metric strength of an event is determined by the number of levels of the metric hierarchy that coincide with it.
Povel has also proposed that this mechanism implies a kind of hierarchy of adjustable internal clocks that organize the rhythmic sequence into a beat hierarchy and that can adapt to changes in tempo. Tempo fluctuations are called rubato in music; but, in spite of these fluctuations, we don't have any trouble following the beat structure. That this is so is evidenced by the fact that people don't tend to stumble over the beat when dancing to even the most fluctuating Viennese waltzes. Similar dramatic fluctuations can be found in the musics of many cultures. A particularly remarkable example is the gamelan music of Java. The extraction of pulse and metric hierarchy is a highly culture-specific phenomenon as Arom (1991) has shown for the complex polyrhythms played by the Aka Pygmies in Central Africa.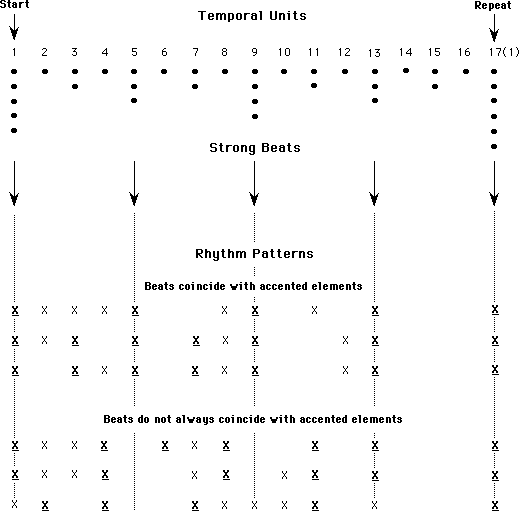
Figure 13. Examples of correspondence and conflict between subjective accents resulting from grouping and from the underlying meter. Events in a rhythmic pattern are marked with an X. Underlined X's are heard as accented due to the grouping structure. [From Fig. 11.4, Handel (1989). (c) MIT Press. Adapted with permission.]
Once a metric framework is well established, it can organize a temporal sequence even when few notes fall directly on the beats. This kind of situation is call syncopation, which gives a particularly exciting feel to a lot of African and Latin American music as well as to various styles of jazz. In these musics, the long periods where many important notes fall off the beat, create a great rhythmic tension that is then suddenly released when a strong beat of the underlying meter is reaffirmed by a note falling directly on it.
Serafine et al. (1989) have made an elegant demonstration of the psychological reality of a hierarchical mental representation of musical passages. They took melodies composed by Bach and simplified them to different degrees by a process similar to the time-span reduction in Lerdahl and Jackendoff's (1983) theory. For each reduction, "foil" reductions were also constructed that were similar to the "true" ones but included notes from the original melody that implied a different harmonic progression. Listeners had to identify the reductions that best corresponded to the original melody. That is, can one recognize the reduced version that corresponds to a given melody? Identification was better for the less reduced structures indicating certain limits in the hierarchical level at which such direct comparisons between melodies and reductions can be made. In a similar experiment conducted by Bigand (1990) listeners were able to judge the similarity between melodies that had different surface characteristics but that were derived from the same underlying structure as would be the case in the recognition of the relation between different variations on a theme.
Figure 14. Theme and elaborated variation played by the violins in Beethoven's 6th Symphony. The theme may be considered a structural "reduction" of the variation.
As with time span reduction, little research has explicitly tested this hypothesis, but there are nonetheless a few encouraging results. Bigand (1993b) has found that melodies constructed such that their underlying structures evoke the same tension/relaxation hierarchy are perceived as being more similar than melodies that have similar surface features but different underlying structures. Musicians and nonmusicians are able to estimate the degree of tension and relaxation of a given note in a melody with a remarkable precision and with a very good agreement among their judgments. Figure 15 shows the average estimates of musical tension given by listeners in response to two melodies that differ only in their rhythmic structure. These estimations correspond very well qualitatively to the structures predicted by the theory. In addition, a change in the rhythmic structure strongly affects the tension/relaxation hierarchy in terms of the independent contributions to the event hierarchy of the tonal hierarchy and the time-span segmentation. Notes that have a strong position in the tonal hierarchy tend to fall on strong beats in the melody in the upper panel and on weak beats in the lower panel. It is worth noting that for several runs of notes that have identical rhythmic structures in the two melodies, the fact that the position within the meter is different engenders large differences in perceived musical tension. This confirms the musician's intuition that the final percept depends on the convergence of both temporal and pitch information.
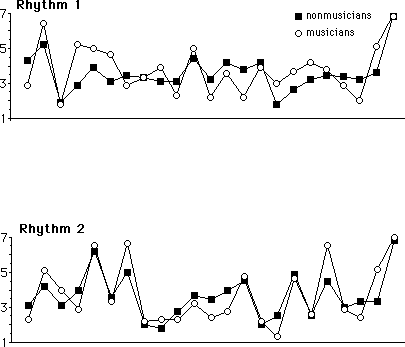
Figure 15. Musical stability profiles for musicians and nonmusicians. Higher ratings indicate greater stability or relaxation and lower ratings greater tension. The same melodic pattern was presented with two different rhythms which engendered significant changes in stability ratings. [From Fig. 7, Bigand (1993b). (c) Harwood Academic Press. Adapted with permission.]
Bharucha JJ (1987) Music cognition and perceptual facilitation: A connectionist
framework. Music Perception 5:1-30.
Bharucha JJ, Krumhansl CL (1983) The representation of harmonic structure in
music: Hierarchies of stability as a function of context. Cognition
13:63-102.
Bharucha JJ, Olney KL (1989). Tonal cognition, artificial intelligence, and
neural nets. Contemporary Music Review 4:341-356.
Bharucha JJ, Stoeckig K (1986). Reaction time and musical expectancy: Priming
of chords Journal of Experimental Psychology: Human Perception and Performance
12:1-8.
Bigand E (1990). Abstraction of two forms of underlying structure in a tonal
melody. Psychology of Music 18:45-60.
Bigand E (1993a) Contributions of music to research on human auditory
cognition. In: Thinking in sound: The cognitive psychology of human audition
(McAdams S, Bigand E, eds.), pp. 231-277. Oxford:Oxford UP.
Bigand E (1993b) The influence of implicit harmony, rhythm, and musical
training on the abstraction of `tension-relaxation schemas' in tonal musical
phrases. Contemporary Music Review 9:123-138.
Blackwell HR, Schlossberg H (1943) Octave generalization, pitch discrimination,
and loudness thresholds in the white rat. Journal of Experimental Psychology
33:407-419.
Botte MC, McAdams S, Drake C (1994) La perception des sons et de la musique.
In: Perception et agnosies: Séminaire Jean-Louis Signoret (Lechevalier
B, Eustache F eds.), pp. 55-99. Brussels: De Boeck.
Boulez P (1987) Timbre and composition - timbre and language. Contemporary
Music Review 2:161-172.
Bregman AS (1990) Auditory scene analysis: The perceptual organization of
sound. Cambridge, MA: MIT P.
Bregman AS (1993) Auditory scene analysis: Hearing in complex environments. In:
Thinking in sound: The cognitive psychology of human audition (McAdams S,
Bigand E, eds.), pp. 10-36. Oxford:Oxford UP.
Clarke EF, Krumhansl CL (1990) Perceiving musical time. Music Perception
7:213-252.
Deliège I (1987) Grouping conditions in listening to music: An approach
to Lerdahl and Jackendoff's grouping preference rules. Music Perception
4:325-60.
Deliège I, El Ahmadi A (1990) Mechanisms of cue extraction in musical
groupings: A study of Sequenza VI for Viola Solo by Luciano Berio. Psychology
of Music 18:18-44.
Demany L, Armand F (1984) The perceptual reality of tone chroma in early
infancy. Journal of the Acoustical Society of America 76:57-66.
Donnadieu S, McAdams S , Winsberg S (1994) Caractérisation du timbre des
sons complexes. I: Analyse multidimensionnelle. Journal de Physique
4(C5):593-596.
Dowling WJ, Harwood D (1986) Music Cognition. Orlando, FL: Academic P.
Dowling WJ, Lung KM, Herrbold S (1987) Aiming attention in pitch and time in
the perception of interleaved melodies. Perception and Psychophysics 41:642-56.
Drake C, Botte MC (1993) Tempo sensitivity in auditory sequences: A tentative
model of regularity extraction. Perception and Psychophysics 54:277-286.
Ehresman D, Wessel DL (1978) Perception of timbral analogies. Rapport IRCAM,
vol. 13 [unpublished technical report].
Fraisse P (1963) Psychology of time. Harper: New York [trans. from Psychologie
du temps. Paris: Presses Universitaires de France, 1957].
Giard MH, Collet L, Bouchet P, Pernier J (in press) Signs of auditory selective
attention in the human cochlea. Brain Research.
Grey JM (1977) Multidimensional perceptual scaling of musical timbres. Journal
of the Acoustical Society of America 61:1270-1277.
Handel S (1989) Listening: An introduction to the perception of auditory
events. Cambridge, MA: MIT P.
Jordan D, Shepard RN (1987) Tonal schemas: Evidence obtained by probing
distorted musical scales. Perception and Psychophysics 41:489-504.
Kameoka A, Kuriyagawa M (1969) Consonance theory. Part II: Consonance of
complex tones and its calculation method. Journal of the Acoustical Society of
America 45:1460-1469.
Krimphoff J, McAdams S, Winsberg S (1994) Caractérisation du timbre des
sons complexes. II: Analyses acoustiques et quantification psychophysique.
Journal de Physique 4(C5):625-628.
Krumhansl CL (1979) The psychological representation of musical pitch in a
tonal context. Cognitive Psychology 11:346-74.
Krumhansl CL (1989) Why is musical timbre so hard to understand? In: Structure
and perception of electroacoustic sound and music (Nielzén S, Olsson O,
eds.), pp. 43-53. Amsterdam: Elsevier (Excerpta Medica 846).
Krumhansl CL (1990) Cognitive foundations of musical pitch. Oxford: Oxford
UP.
Krumhansl CL, Jusczyk PW (1990) Infants' perception of phrase structure in
music. Psychological Science 1:70-73.
Krumhansl CL, Kessler E (1982). Tracing the dynamic changes in perceived tonal
organization in a spatial representation of musical keys. Psychological Review
89:334-68.
Lerdahl F (1987) Timbral hierarchies. Contemporary Music Review 2(1):135-160.
Lerdahl F, Jackendoff R (1983) A generative theory of tonal music. Cambridge,
MA: MIT P.
Marín OSM (1982) Neurological aspects of music perception and
performance. In: The psychology of music (Deutsch D, ed.), pp. 453-478. New
York: Academic P.
Mathews MV, Pierce JR , Roberts LA (1987) Harmony and new scales. In: Harmony
and Tonality (Sundberg J, ed.), pp. 59-84. Stockholm: Royal Swedish Academy of
Music, publ. no. 54.
McAdams S (1987) Music: A science of the mind? Contemporary Music Review
2(1):1-61.
McAdams S (1989) Psychological constraints on form-bearing dimensions in music.
Contemporary Music Review 4:181-98.
McAdams S (1993) Recognition of sound sources and events. In: Thinking in
sound: The cognitive psychology of human audition (McAdams S, Bigand E, eds.),
pp. 146-198. Oxford:Oxford UP.
McAdams S, Bigand E (eds.) (1993) Thinking in sound: The cognitive psychology
of human audition. Oxford:Oxford UP.
McAdams S, Cunibile JC (1992) Perception of timbral analogies. Philosophical
Transactions of the Royal Society, London, Series B 336:383-389.
Meyer LB (1956) Emotion and meaning in music. Chicago: U Chicago P.
Parncutt R (1989) Harmony: A psychoacoustical approach. Berlin: Springer
Verlag.
Peretz I (1993) Auditory agnosia: A functional analysis. In: Thinking in sound:
The cognitive psychology of human audition (McAdams S, Bigand E, eds.), pp.
199-230. Oxford:Oxford UP.
Plomp R, Levelt WJM (1965) Tonal consonance and critical bandwidth. Journal of
the Acoustical Society of America 38:548-560.
Povel DJ (1984) A theoretical framework for rhythm perception. Psychological
Research 45:315-37.
Puel JL, Bonfils P, Pujol R (1988) Selective attention modifies the active
micromechanical properties of the cochlea. Brain Research 447:380-383.
Serafine ML, Glassman N, Overbeeke C (1989) The cognitive reality of hierarchic
structure in music. Music Perception 6:397-430.
Shepard RN, Metzler J (1971) Mental rotation of three-dimensional objects.
Science 171:701-703.
Sloboda JA (1992) Empirical studies of emotional response to music. In:
Cognitive bases of musical communication (Jones MR, Holleran S, eds.), pp.
33-46. Washington, DC: American Psychological Association.
Thorpe LA, Trehub SE, Morrongiello BA, Bull D (1988) Perceptual grouping by
infants and preschool children. Developmental Psychology 24:484-91.
Tramo M, Bharucha J, Musiek F (1990) Music perception and cognition following
bilateral lesions of auditory cortex. Journal of Cognitive Neuroscience
2:195-212.
Zatorre RJ (1989) Effects of temporal neocortical excisions on musical
processing. Contemporary Music Review 4:265-278.
Laboratoire de Psychologie Expérimentale (CNRS), Université
René Descartes, EPHE,
28 rue Serpente, F-75006 Paris, France
and IRCAM, 1 place Stravinsky, F-75004 Paris, France
____________________________ ____________________________
Stephen McAdams
Server © IRCAM-CGP, 1996-2008 - file updated on .
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .