Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved.

Introduction

• d'une part sur la description physique des phénomènes, c'est à dire le matériau,
• d'autre part sur l'articulation de ces phénomènes, c'est à dire l'organisation et finalement la composition.

Cette recherche de modèles a pour but de permettre ce que nous considérons comme l'aboutissement et le dépassement de la simulation: l'extrapolation de nouveaux modèles créatifs pour la musique, à partir des modèles cognitifs élaborés grâce à la méthodologie de la synthèse par règles. La synthèse étant alors aussi bien l'épreuve de notre compréhension du fonctionnement des phénomènes, que celle de la musique elle-même. Nous réexaminerons donc la problématique de la synthèse de la façon suivante:

• dans la première partie nous reconsidérons certains des choix qui ont orienté le développement de techniques et de programmes de synthèse. Nous expliquons les raisons qui nous ont conduits à prendre comme point de départ un modèle physique de production de sons, la voix, du fait de sa généralité et de sa complexité,
• dans la seconde partie nous présenterons et comparerons deux types d'implémentation (filtres et fonctions d'ondes formantiques) du synthétiseur inspiré par ce modèle de production,
• dans la troisième partie nous décrirons le programme de synthèse par règles CHANT, contrôlant ce synthétiseur, et des exemples de travaux réalisés desquels se dégagent les notions de modèles et de règles, d'objets et de processus, dont l'importance a conduit à la conception et à la réalisation du programme FORMES.

1. Reconsidération des techniques et des programmes et choix d'un modèle de production

1.1 Reconsidération des techniques et des programmes

Par exemple:

• L'imitation de techniques analogiques
  Paradoxalement en effet, les moyens analogiques ont souvent été d'un emploi plus simple que bien des programmes. Les modules peuvent être reliés les uns aux autres par un simple câble (ce qui n'est pas le cas des sous-programmes, à cause notamment du passage des arguments). L'effet attendu est presque toujours obtenu sans le recours à un code mystérieux. Enfin le contrôle se fait d'un geste sur un potentiomètre par exemple. Une telle approche, cependant n'utilise que très pauvrement les immenses possibilités des traitements de signaux numériques, les capacités de traitement formel des langages informatiques ou de leurs structures de contrôle.
• La rapidité de calcul
  Ce souci était particulièrement justifié au début de la musique informatique, le matériel étant lent et non spécialisé pour la synthèse. Mais favoriser la rapidité de calcul peut avoir plusieurs conséquences néfastes. En premier lieu, une technique visant la rapidité est en général sans rapport avec les propriétés de la perception. D'où une grande difficulté de contrôle des caractéristiques perceptives du son, puisqu'elles dépendent des paramètres de la méthode de synthèse à travers une relation très complexe et arbitraire. L'apprentissage d'une telle méthode de synthèse est alors long et injustifié. Par contre, une technique particulière favorise généralement une famille spécifique de sons qui seront difficilement réalisables avec une autre technique. Ce qui se définirait comme un coefficient d'idiomaticite. En second lieu, une technique visant la rapidité est en général sans rapport non plus avec le mode de production des sons naturels (cf: modèles physiques), ce qui aggrave également les problèmes d'utilisation. Car on ne peut alors se fonder sur notre connaissance des relations entre les variations du mode de production et les variations correspondantes du son. De plus l'évolution des composants électroniques autorise désormais, pour un faible coût, des puissances de calculs considérables. La limite des calculs possibles est donc sensiblement repoussée.
• La représentation patch-liste de note-fonctions
  Ce choix a plusieurs conséquences. Une des difficultés réside dans l'explicitation des niveaux de contrôles intermédiaires entre le patch et la liste de notes. En effet un patch peut permettre de décrire de manière assez satisfaisante un instrument ou un synthétiseur. Mais en revanche les langages de patch déjà existants sont assez pauvres pour décrire des niveaux de contrôle évolués, du type fonction d'interprétation (par exemple: expressivité, décisions en fonction du contexte, qualité du timbre, intonation, accentuation, nuances, etc...).

  Pour offrir une possibilité de jeu véritable sur le son, il faut alors constituer un instrument d'une complexité très élevée, donc contrôlé par un grand nombre de paramètres. A tel point qu'écrire une seule note devient presque impossible. A la lourdeur de la description vient s'ajouter la lourdeur du temps de calcul quand le calcul s'effectue à l'échantillon. Or les fonctions de contrôle ont des variations relativement lentes: en moyenne 1OOhz. Dans les langages de la famille de «Music V» ce type de contrôle est aussi réalisé par des fonctions. Mais celles-ci ne sont plus alors des descriptions algorithmiques, contrairement au patch. Ainsi des corrélations entre paramètres ne peuvent plus être prises en compte. De plus leur portée temporelle est assujettie à la durée de la note. Ce qui rend ainsi acrobatique des contrôles de paramètres de façon continue, à travers les notes (par exemple dans le cas d'un legato) ou l'utilisation de fonctions dont la portée veut être différente de la durée d'une note (par exemple un crescendo sur une phrase entière]. Il semble donc manquer un niveau de contrôle intermédiaire, entre le patch et le niveau organisationnel de la note. Ce niveau devrait pouvoir être décrit dans un langage de programmation et permettre toute interaction entre son et perception, entre matériau et organisation.

Ce sont ces remarques qui nous ont amenés à envisager, d'une part le choix d'un modèle de production, la voix, et d'autre part le choix d'une méthodologie, la «synthèse par règles».

Le choix de la voix comme modèle de production s'impose du fait de sa richesse extrême, qui par la multiplicité de ses productions, la variété des utilisations musicales et langagières qui en découlent, sucite et permet une approche plus générale et féconde que l'étude d'un autre instrument aussi complexe soit-il. C'est ainsi la nécessité de rendre compte pleinement de la complexité des variations du modèle vocal, et plus particulièrement du résonateur, qui va forcer à atteindre la généralité qui ultérieurement permettra de dériver vers d'autres modèles pourtant très différents.

Nous allons donc maintenant envisager le fonctionnement de l'appareil vocal et sa modélisation pour examiner ensuite les choix qui ont été faits à partir de cette référence pour la réalisation du synthétiseur et du programme «CHANT».

1.2 Description du fonctionnement de l'appareil vocal: un modèle de production

La production de la parole, comme celle de nombreux sons ou signaux, est donc souvent représentée par un modèle comportant une source d'excitation et un filtre linéaire, non couplés (cependant il est souhaitable, sinon indispensable, que de tels couplages soient pris en compte: cf. (Carré) et (G. Weinreich).

Le filtre F¹, généralement linéaire, est caractérisé par sa fonction de transfert H¹ qui varie continuellement (Fig.1). Elle tient compte notamment des caractéristiques du système matériel qui est excité (conduit vocal, caisse de résonance, etc.) et de son rayonnement sonore.

Figure 1 - Amplitude (log) de la fonction de transfert H1.

Figure 2 - Amplitude (log) du spectre de la source voisée P.

Dans le cas de la voix, le modèle comporte une source périodique P pour les sons voisés et une source aléatoire s pour les sons fricatifs ou plosifs et pour le souffle. Une source est caractérisée essentiellement par son spectre d'amplitude (Fig.2). On peut le décrire également au moyen d'un filtre F2 qui représente son enveloppe, et d'une source P2 (et s2) à spectre plat X(f). Les deux filtres F2 et F1 en cascade peuvent alors être regroupés en un seul filtre F. Le spectre de l'onde résultante est alors le produit du spectre de la source par le gain du filtre:

Y [f) = X (f) . H (f) (Fig.3)

Figure 3 - Amplitude (log) du spectre de la forme d'onde de sortie.

Le cas d'une source glottale montre bien l'intérêt, d'un modèle de production ([Fant] et [Rothenberg]). Mais si on se limite à un tel modèle, on n'obtiendra qu'une famille limitée de sources. Pour des applications musicales, l'imagination ne doit pas être limitée. Il est donc intéressant de formaliser ce modèle dans le domaine spectral, puis de l'inclure dans un modèle plus général décrivant le spectre de la source. Ce modèle général est contrôlé par des paramètres directement liés aux caractéristiques du spectre dont on peut prévoir facilement les conséquences perceptives. A titre d'exemple: dans chaque bande de fréquence, amplitude et pente de l'enveloppe spectrale, rapport des amplitudes des harmoniques pairs et impairs, inharmonicité, variations aléatoires, etc.

Le conduit vocal est une sorte de tube d'environ 17 cm de long, de section variable, avec une dérivation vers le conduit nasal. De façon simplifiée, il peut être assimilé à une série de N résonateurs en cascade et M en dérivation. Son gain ou fonction de transfert présente donc en général N maxima appelés formants. Le caractère plus ou moins pointu de ces maxima est mesuré par leur largeur de bande à mi-hauteur du sommet (- 3 db).

Le spectre d'amplitude de l'onde sonore émise présente donc lui aussi, en général, des maxima correspondant aux formants. L'importance de ces formants tient non seulement à ce qu'ils dérivent de la forme du conduit vocal à chaque instant (pour chaque articulation), mais encore à leur prépondérance au niveau perceptif: en raison des propriétés de l'oreille (masquage notamment) les parties du spectre qui présentent de tels maxima sont bien représentées par la fréquence, l'amplitude et la largeur de bande des formants.

Nous allons examiner les détails de deux implémentations de la technique de synthèse, par filtres numériques et par fonctions d'onde formantiques. Puis nous comparerons ces deux implémentations.

2. Le synthétiseur chant

2.1 Filtre numérique

H(z)=( ₀+ ₁z^-1 +...+ _qz^-q)/(1+₁ z^-1+ ... + _pz^-p)

qui comporte p pôles et q zéros. C'est le cas par exemple en prédiction linéaire ([Moorer]). La réalisation d'un tel filtre numérique et le calcul de ses paramètres a et b présentent des difficultés dont nous parlerons ultérieurement. En conséquence, on peut utiliser une autre forme:

H(z)=c_i(1+d_iz^-1) / (1+a_iz^-1+b_i z^-2).

Le filtre H se présente alors comme un ensemble de J cellules en parallèle (Fig.4). Chaque cellule est constituée d'un filtre du 1^er ordre (un zéro) et d'une section du 2^eme ordre (2 pôles) en série, avec un gain c.

Figure 4 - Représentation du filtre en parallèle H.

Chaque cellule est de réalisation très simple. Le calcul des paramètres est aussi beaucoup moins complexe. Enfin ils permettent de contrôler directement et de façon simple les caractéristiques perceptuellement intéressantes de l'enveloppe du spectre (Fig.5):

• a et b déterminent la fréquence centrale d'une bande f de l'enveloppe du spectre et sa forme locale (maximum et largeur de bande, ou replat),
• c contrôle l'amplitude globale de cette zone,
• d permet d'incliner dans un sens ou dans l'autre, l' enveloppe dans cette zone.

Figure 5 - Amplitude (log) des différentes fonctions de transfert d'une cellule.

2.2 Fonctions d'onde formantiques (FOF)

E (k) = e_n(k)

(où n indexe les impulsions successives), alors la réponse S du filtre précédent peut être calculée facilement comme la somme des réponses s_n(k) décalées d'une période du fondamental T = 1 /FO (FO est la fréquence fondamentale de l'excitation et de la réponse) (Fig.6). Une réponse s_n(k) est elle-même la somme des J réponses partielles des cellules disposées en parallèle:

s(k) = s_n,i(k)

Figure 6 - Construction de la réponse S comme somme des réponses Sn.

où les s_n,i(k) sont appelés fonctions d'onde formantiques (FOF) car elles correspondent en général aux formants ou modes de résonance principaux du système.

Les variations de fréquence fondamentale sont obtenues en variant les durées de périodes fondamentales T = 1 /fO, c'est à dire les débuts des FOF successives. Les variations de l'enveloppe du spectre sont obtenues en modifiant les FOF partielles.

2.3 Calcul des FOF

C(1+d_iz^-1)/ (1+_iz^-1+b_iz^-2) =C_i(1+d_iz^-1)/((1-r_iz^-1)(1-r_iz^-1))

-k

• = -1/2 log b_i
• w= Arg r_i
• =Arctg{sin(w.e^-)/(d_i - a_i - cos(w.e^-))}
• G=C_i/sin

Ainsi une FOF s'obtiendrait simplement comme le produit d'une sinusoïde par une enveloppe exponentielle. Cependant, pour les sons naturels, I'excitation n'est pas une impulsion unitaire. Pour obtenir un contrôle plus précis sur le spectre, nous avons utilisé la FOF suivante (Fig.7):

• s(k)=0 pour : k<0
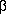• s(k)= 1/2(1 - cos ( k)).e^-k sin (wk + ) pour:0 k /
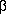
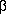• s(k)=e^-k sin(wk + ) pour: / < k

Figure 7 - Une fonction d'onde formantique.

C'est encore une sinusoïde multipliée par une enveloppe A(k). Cette enveloppe est une exponentielle amortie dont la discontinuité initiale est lissée par multiplication par 1/2 (1 - cos ( 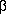k)) sur une durée de / échantillons. On obtient ainsi une enveloppe d'amplitude A (k):

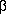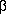• qui présente une attaque d'une durée de / échantillons et un amortissement général en exp (-k)
• qui ne présente pas de discontinuité du 1^er ni du 2^eme ordre,
• qui peut être obtenue très simplement par lecture de table et par une multiplication par C = exp (-) pour exp (-k).

• w est la fréquence centrale du maximum,
• est la largeur de bande à -3 db,
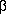• règle la largeur des jupes ou la pente de l'attaque.

Figure 8 - Amplitude (log) du spectre d'une FOF A(k) sin(wk+) pour différentes valeurs de / (w₀=2500 Hz, =80 Hz).

1. / =10 ms
2. / =1 ms
3. / =0.01 ms

2.4 Synthétiseur FOF

• 2 w, fréquence centrale
• BW_i, largeur de bande
• A_i amplitude
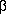• / _i, largeur de jupes
• _i phase initiale.

Figure 9 - Structure d'un synthétiseur FOF.

2.5 Comparaison du modèle FOF et du modèle filtre

Il y a de plus une différence intéressante. Nous avons toujours utilisé, à l'intérieur de chaque FOF partielle s_n,i(k) une fréquence w constante (une fréquence variable permet des effets intéressants d'élargissement du spectre). Or un résonateur continûment variable comme le conduit vocal devrait être modélisé par un filtre continûment variable, donc un w variable à l'intérieur d'une FOF partielle. En pratique, pour les sons vocaux et la plupart des sons instrumentaux, la durée de chaque période est si courte par rapport aux vitesses de variation des w que la différence n'est pas perceptible. Mais il faut d'abord noter que dans un filtre, les coefficients ne doivent pas subir de discontinuité, donc, doivent être interpolés entre chaque nouvelle valeur (tandis qu'en FOF on peut se contenter d'une nouvelle valeur à chaque période, les FOF étant nondiscontinues par construction). Ensuite, la différence entre les deux méthodes apparaît lorsque la largeur de bande BW est très faible et que w varie, rapidement. La réponse d'une cellule du filtre est alors presque une sinusoïde dont la fréquence centrale évolue continûment. Par contre, les s_n (k) déclenchées à chaque période n sont presque des sinusoïdes (amortissement très faible si la largeur de bande est très faible) de fréquences, chacune fixe, mais différente de la précédente: le spectre présente alors des raies très serrées donnant un son beaucoup plus riche que la quasisinusoïde sortant du filtre (Fig.10).

Figure 10 - Comparaison des modèles FOF et filtre pour de petites largeurs de bande et une évolution rapide en fréquences(a) modèle filtre.

C'est un moyen aisé pour obtenir un son riche dans une certaine bande ne fréquence sans avoir à préciser chacune des raies. On obtient ainsi une famille intéressante de sons. Nous avons, par exemple, synthétisé de la sorte des cymbales.

2.6 Discussion du modèle de synthèse en parallèle

Lorsqu'on place les J cellules en parallèle, on attend du module du gain complexe total qu'il soit la somme de ceux des cellules individuelles (ou des FOF). Ce n'est pas nécessairement le cas (Fig.11), car certaines composantes peuvent se trouver en opposition de phase, donc s'annuler. Cela se produit essentiellement entre les fréquences centrales de deux cellules voisines (Fig.12), où l'on voit apparaître un «trou» (un zéro) dans le spectre. On observe qu'on peut remédier à ce défaut en déphasant la réponse d'une cellule par rapport à l'autre (Fig.13). Ce déphasage est particulièrement simple dans la méthode FOF puisqu'il suffit de positionner correctement la phase initiale de la sinusoïde dans chaque cellule.

Figure 11 - Comparaison d'un modèle du gain complexe total avec la somme des modules des cellules individuelles.

Figure 12 - Présence d'un «zéro» entre les fréquences centrales de deux cellules voisines.

Figure 13 - Déphasage de la réponse d'une cellule en rapport avec l'autre.

Pour le modèle filtre, nous avons étudié un grand nombre de configurations de pôles et de zéro pour déphaser les cellules les unes par rapport aux autres. Mais on doit écarter l'utilisation de filtres déphaseurs, car ils sont ou inadéquats ou trop complexes, ce qui irait dans le sens contraire de la simplicité qui motive le modèle en parallèle. Par contre, on peut utiliser autant de sources qu'il y a de cellules, et leur déphasage est alors simple (par exemple, c'est la valeur initiale de l'index si on utilise une lecture de table).

Figure 14 - Sources individuelles pour chaque cellule du modèle parallèle.

C'est en particulier la solution que nous avons choisi pour l'implantation du programme CHANT sur le Systems Concepts Digital Synthetizer (Samson-Box) du C.C.R.M.A. à Stanford (Fig.14) (Grâce à l'accueil et à l'aide de John Chowning et John Gordon). En effet les générateurs peuvent produire, avec une phase initiale contrôlable, une impulsion périodique à spectre plat et à bande limitée.

Cette dernière caractéristique, aussi, est importante, car un filtre en parallèle tend à avoir un gain plus élevé que le filtre série de mêmes caractéristiques dans la zone de fréquence située au delà du formant de fréquence maximale (Fig.11): en effet, les gains des cellules s'ajoutent au lieu de se multiplier comme c'est le cas dans un modèle série (le problème n'apparaît pas en FOF grâce au contrôle des largeurs de jupe par B, donc au contrôle de l'amplitude du spectre au delà du formant de fréquence maximale).

L'octroi d'une source individuelle à chaque cellule est encore souhaitable pour permettre le contrôle, dans chaque bande de fréquence d'autres caractéristiques du spectre comme: inharmonicité, largeur de jupe, etc.

On peut également faire varier l'importance respective d'une certaine classe de partiels par rapport à une autre. A titre d'exemple, les harmoniques pairs et impairs: supposons qu'une source soit composée de deux trains d'impulsions T1 et T2 de fréquences Fo et 2Fo, et d'amplitudes respectives A1 et A2 (Fig.16). Le spectre correspondant au premier est un spectre de raies Fo, 2Fo, 3Fo,... et le second de raies 2Fo, 4Fo, 6Fo, ... Le spectre correspondant au train T1 +T2 est la somme des spectres respectifs de T1 et T2.

Figure 15 - Ensemble d'impulsions pour varier les tailles respectives des partiels pairs ou impairs.

Ainsi, en sommant ces deux spectres on peut, accroître l'intensité des raies paires si A1 et A2 sont de même signe, ou la diminuer (éventuellement; jusqu'à zéro) s'ils sont de signes opposés. Ceci revient à dire que le train d'impulsion à utiliser, somme des trains 1 et 2, est de fréquence 2Fo et d'amplitude, alternativement A1 + A2 et A1 pour les impulsions successives. On a ainsi, par un simple contrôle de l'amplitude des impulsions, un contrôle des raies paires et impaires et ceci dans chaque bande de fréquence (cf. octaviation).

Enfin, dans le cas où le filtre en parallèle est utilisé pour le traitement d'un signal, on peut déduire de ce signal J signaux qui serviront de sources aux J cellules. En stockant le signal d'origine dans une table et en le lisant avec des index déphasés on crée autant de sources déphasées. On peut également introduire d'autres variations, d'amplitude par exemple, spécialement si chaque période fondamentale peut être détectée de façon sûre; mais ce dernier point est délicat.

2.7 Nécessité d'une arithmétique flottante

Nous n'en déduisons pas que le modèle en série doive être abandonné. Au contraire, car le modèle en parallèle, nous l'avons vu, présente ses propres difficultés. Mais les synthétiseurs musicaux doivent inclure une arithmétique flottante très rapide et les opérations dont aucun ordinateur moderne ne se passe. La technologie actuelle le permet en effet pour un coût qui devient abordable et qui ne cesse de décroître. D'ailleurs, le surcoût est largement compensé par la puissance et la souplesse que gagne alors le synthétiseur.

Deux autres arguments plaident en faveur de l'arithmétique flottante. D'abord, il faut bien ajuster le niveau du signal pour la conversion numérique-analogique: qui n'a pas souffert de sons saturés ou inaudibles et perdu beaucoup de temps à ajuster des coefficients magiques de gain ? Dans un synthétiseur travaillant pour une bonne part en flottant, il suffit d'une passe «à vide» pour détecter l'échantillon d'amplitude maximum, en déduire le gain, et faire entendre, sans intervention humaine, un son dont le niveau est ajusté de façon optimale. C'est le cas dans le programme CHANT: sauf décision volontaire, le son n'est jamais saturé ni inaudible, et c'est un facteur de rentabilité et d'agrément considérable.

Le second argument concerne le calcul des paramètres. C'est à dire tous les paramètres qui précèdent la synthèse proprement dite. Ces algorithmes peuvent atteindre une grande complexité: quand on veut tendre vers la finesse d'interprétation traditionnelle, lorsqu'on veut maîtriser tous les détails du son et ses relations subtiles avec l'organisation. Là encore, ces algorithmes ne peuvent se résumer à quelques lectures de tables et interpolations. De plus, I'utilisateur doit être débarrassé de tout souci de dynamique des calculs et autres débordements (les algorithmes et la musique sont déjà bien assez complexes et ne pourront qu'y gagner). En conséquence, ce calcul des paramètres doit utiliser, lui aussi, une arithmétique flottante et rapide. Nous verrons de plus qu'il requiert un logiciel évolué.

Ainsi l'outil informatique peut se prêter aux utilisations les plus extrêmes, et les plus inattendues C'est un mérite du programme CHANT que d'accepter des paramètres qui ont, tant que possible, un sens immédiat. De plus il suffit de positionner des paramètres à des valeurs qui ne soient pas absurdes du point de vue physique et perceptuel pour obtenir un son à la fois attendu et d'une richesse surprenante.

3. Le programme chant

3.1 Description générale du programme

Dans le premier cas l'utilisateur spécifie simplement les valeurs de paramètres pré-existants, dans le second il bénéficie de toute la puissance d'un langage de programmation pour créer de nouvelles règles ou décrire l'évolution des paramètres de manière algorithmique dans des sous-programmes.

Dans la version de base, CHANT comporte une centaine de paramètres, mais beaucoup peuvent rester inchangés d'un son à l'autre, et sont par conséquent définis avec des valeurs par défaut, ce qui permet une extrême facilité d'utilisation.

Ces paramètres peuvent être regroupés sous les rubriques: fréquence du fondamental, variations aléatoires du fondamental, vibrato, variations aléatoires du vibrato, spectre: formants et fondamental, pente du spectre, calcul automatique du spectre, intensité du son, enveloppe locale des formants, et enfin contrôle sur la synthèse.

Chaque paramètre peut être défini soit par une valeur fixe, c'est-à-dire une constante, soit par une fonction du temps (fonction par segments), qui associe une valeur donnée à un temps donné et permet par conséquent l'interpolation d'une valeur à une autre.

Ces paramètres et leurs valeurs sont stockés dans un fichier, alors appelé fichier de paramètres. Certains autres fichiers peuvent ne contenir que des fonctions, par exemple des fonctions complexes calculées avec les moyens spéciaux disponibles dans l'Environnement et définis par un grand nombre de points. Ces derniers, appelés fichiers de fonctions, peuvent être appelés d'un fichier central, qui décrira tous les appels.

Ainsi les fichiers peuvent être utilisés de manière modulaire et constituer un véritable réseau, parfois d'une grande complexité.

Notamment par le jeu de facteurs et d'offsets appliqués aux fonctions, les fichiers, extraits de la bibliothèque, peuvent être utilisés comme des modèles desquels on dérive progressivement, par modifications successives, par réajustement des valeurs jusqu'à l'obtention de l'effet désiré.

Le travail de l'utilisateur consiste donc, dans un premier temps, à intervenir dans un fichier de paramètres, soit en définissant directement les valeurs, soit en modifiant les valeurs déjà définies, s'il part d'un fichier préexistant tel ceux disponibles dans la bibliothèque.

Mais ces modifications peuvent aussi être réalisées dans un mode interactif c'est à dire au dernier moment, juste avant de lancer la synthèse. Dans ce cas l'utilisateur donne au programme un fichier de paramètres et modifie alors seulement les valeurs qui l'intéressent. Le fichier original qui a servi de modèle reste intact, mais les modifications sont préservées dans un fichier de sortie produit automatiquement par le programme. Ce fichier de sortie est donc la réplique du fichier d'entrée, avec en plus les modifications insérées dans le mode interactif. Ceci permet un travail évolutif: le fichier de sortie pouvant être utilisé comme entrée et remodifié, ou bien pouvant être conservé pour garder chaque étape de l'élaboration.

Ceci montre le soin particulier qui a été porté, afin de faire de CHANT un instrument évoluable, c'est-à-dire à mémoire: tout travail devant pouvoir être conservé et réutilisé de manière simple et efficace. Ainsi, ces fichiers sont gardés dans une bibliothèque de fichiers de paramètres et de fonctions, qui représente la première partie de ce que nous avons appelé l'Environnement CHANT, qui en outre comprend un catalogue de sous-programmes et de programmes divers, programmes d'analyses variées, de construction de fonctions à partir d'un signal (et réciproquement), de tests rapides, de construction d'un spectre, etc.

La possibilité de conserver le travail accumulé a pour destination de répondre aux mêmes préoccupations que celles qui nous ont fait envisager la définition en termes de modèles, véritables schémas cognitifs d'une production donnée. Car pour être efficace, la définition et l'élaboration de tels modèles, qui sont coûteuses en temps d'expérimentation, doivent conduire à des connaissances facilement accessibles et réutilisables.

Ce premier niveau d'intervention dans CHANT pourrait être appelé constitution de modèle par données, ces données contrôlant les règles, les descriptions algorithmiques sous-jacentes qui forment par défaut dans CHANT le modèle vocal que nous allons décrire. Mais on peut également modifier ce modèle standard par ajouts et/ou éliminations de réglet et algorithmes et ceci constitue un deuxième niveau d'intervention dans CHANT qui pourrait être appelé constitution de modèle par règles et que nous décrirons par la suite.

Envisageons maintenant certaines des règles élaborées pour la constitution du modèle vocal: de celles, assez simples, de timbre des voyelles, jusqu'à celles plus complexes d'effort vocal, c'est à dire de relation entre timbre et amplitude, etc.

3.2 Elaboration du modèle vocal

Un premier travail consiste à définir précisément et à réaliser les timbres, notamment des voyelles, dans la voix chantée, la fréquence et l'amplitude du vibrato, Ies variations aléatoires du fondamental et du vibrato, et les relations entre timbre et amplitude.

Le timbre est d'abord envisagé à partir de l'enveloppe spectrale, elle-même définie en termes de fréquences centrales et d'amplitudes des formants.

Nous représentons l'enveloppe spectrale par ses formants, et il convient de noter que cette représentation se révèle particulièrement économique et parlante pour l'utilisateur, aussi bien au niveau de la compétence que nécessite la compréhension du résultat d'une analyse spectrale (réalisée par un analyseur ou par le système auditif), qu'au niveau de la performance qui est celui de la synthèse.

Les fréquences de formants ont été dégagées de manière précise à travers un travail d'analyse original notamment à l'aide du Phase-vocoder, c'est à dire en extrayant la fréquence et l'amplitude de chaque partiel et en les superposant pour mettre à jour leurs corrélations, et en déduire les fréquences des formants, mais aussi avec les moyens d'analyses plus classiques offerts par les méthodes de Linear Prediction Coding.

Les algorithmes qui ont été implémentés pour la restitution spécifique du modèle vocal, ceci à partir de résultats théoriques et expérimentaux, sont optionnels.

On peut ainsi choisir la détermination automatique des largeurs de bandes qui sont alors calculées à partir des fréquences des formants, suivant une parabole définie sur le spectre par trois points, eux-mêmes paramètrés.

Pour le calcul automatique de l'amplitude des formants, le programme simule des filtres en série, et d'après la fréquence de chacun détermine leurs amplitudes: ainsi lorsque deux formants ou plus se rapprochent leurs amplitudes sont renforcées.

Un formant supplémentaire, appelé complément, peut aussi être assigné automatiquement pour modifier le premier formant et donner plus d'énergie dans le grave, c'est en quelque sorte un formant numéro zéro.

Les variations aléatoires du fondamental sont perceptuellement très importantes. En demandant à des chanteurs de produire des sons absolument sans vibrato nous avons pu étudier les fluctuations aléatoires et non-contrôlées de la fréquence du fondamental. A l'analyse, on observe beaucoup d'irrégularités, quoique la variation ne soit que de l'ordre de + ou - 0,5% de la fréquence fondamentale. On observe également des variations importantes de taille. La fluctuation aléatoire du fondamental suit une distribution proche de 1 /f. Dans le programme CHANT cette fluctuation est modélisée en ajoutant à la fréquence du fondamental un terme dont la valeur varie de façon aléatoire entre des limites données par l'utilisateur. Ce terme a trois composantes, dont chacune est associée à un temps de tirage aléatoire différent. Si à un instant T₀ la valeur d'une composante est égale à c, on détermine par tirage aléatoire la valeur qu'elle aura à l'instant T₀.,+T_c, où T_c est le temps de tirage aléatoire, par exemple toutes les 0.05 secondes. La valeur effective du terme à ajouter à la fréquence fondamentale à chaque instant est la somme des trois composantes à cet instant. Des valeurs typiques pour les trois temps de tirages aléatoires sont de 0.05, 0.111, 1.219 secondes. Nous répartissons l'excursion de la fluctuation aléatoire également parmi les trois composantes. La fluctuation totale se situe typiquement entre + ou -1,1 % et + ou - 3,7% du fondamental pour des voix de femme, et entre + ou -2% et + ou -4% pour des voix d'homme.

Le vibrato est traditionnellement défini comme l'oscillation plus ou moins régulière de la fréquence fondamentale autour d'une fréquence centrale perçue comme hauteur. Dans CHANT on distingue l'amplitude du vibrato, c'est à dire l'excursion autour de la fréquence centrale, et la fréquence du vibrato c'est à dire le taux de répétition de cette excursion, et les variations aléatoires du vibrato qui sont modélisées par un processus similaire à celui utilisé pour les variations aléatoires du fondamental. Le vibrato a paradoxalement un intérêt du point de vue du timbre, et de celui de la reconnaissance de l'identité d'un chanteur, puisqu'il balaie les résonances correspondant aux formants et par conséquent les révélant, les fait entendre. Du point de vue de la synthèse, I'important est de déterminer une évolution temporelle satisfaisante pour la perception qui est très exigeante dans ce domaine, notamment parce que le vibrato joue aussi un rôle important dans l'interprétation.

Un soin particulier a été aussi porté à l'étude des relations entre timbre et amplitude. Quand un chanteur chante fort, le signal émis par les cordes vocales est tout à fait différent de celui produit quand il chante doucement. En l'occurence, ce signal est beaucoup plus riche en hautes fréquences. La même différence subsiste entre les notes de l'aigu d'un registre et celles du grave du registre. Nous avons modélisé ces effets en appliquant une fonction corrective aux amplitudes des formants numéro deux à cinq.

Cette correction est fonction d'une part de l'amplitude générale demandée par l'utilisateur, et d'autre part de la position de la note dans le registre demandé par l'utilisateur. Nous définissons un registre par la fréquence qui correspond au milieu du registre souhaité. Ainsi la même voyelle synthétisée à la même fréquence aura des timbres différents selon le choix de la fréquence qui définit le registre.

Figure 16 - Amplitude (log) du spectre de la voyelle /a/ à haute amplitude.

Figure 16b - Amplitude (log) du spectre de la voyelle /a/ à amplitude basse.

Les Figures 16a et 16b montrent les spectres de deux sons synthétisés par le programme. Le fondamental est de 300 hz, la voyelle [a]. Dans la Figure 16a, I'amplitude est au maximum, dans la suivante elle est à 18 db au-dessous. On remarquera la différence dans l'amplitude des formants aigus.

La relation entre timbre et amplitude est aussi importante perceptuellement comme indication de la distance d'un son. Si l'on applique une correction de spectre correspondant à un son fort, tout en utilisant pour la synthèse une amplitude faible, on entend le son comme lointain.

3.3 Le modèle par règles

Ces règles constituent la base des modèles, que l'on voudra d'une part construits de façon modulaire, par assemblage de règles, et d'autre part sensibles au contexte.

Pour illustrer ce point, nous envisagerons quelques exemples extraits de deux sous-programmes déjà complexes: la première pour simuler une voix de soprano avec quelques éléments du phrasé et de la technique du chant classique et la seconde une voix inspiré du chant tibétain, introduisant la simulation de l'articulation consonnantique, et surtout un travail original sur le timbre.

Pour la voix de soprano, on a tout d'abord privilégié l'étude sur le placement des formants, typique de l'émission du bel canto. A partir d'analyses réalises au moyen du Phase-vocoder, sur une même hauteur interprétée par plusieurs chanteuses, on a pu obtenir précisément les fréquences des 6 premiers formants. Finalement, on a décidé de garder les fréquences des 6 derniers formants, et on a dégagé pour les deux premiers la relation suivante entre fréquences des formants et hauteur de la note: le premier et le deuxième formants sont; placés respectivement sur les premier et deuxième harmoniques sauf si la fréquence obtenue est; inférieure à un seuil fixé pour chacun d'eux. Ce modèle permet une couleur vocalique homogène sur une grande tessiture, environ deux octaves.

Puis le travail de modélisation a porté sur l'établissement de règles contraignant l'évolution des divers paramètres de la source au cours de staccatos.

Notamment, ces règles s'attachent à décrire les évolutions:

• de la hauteur moyenne, par le dessin d'un portamento interne,
• du vibrato, par croissance puis décroissance de son amplitude et de sa fréquence,
• de l'énergie, par une enveloppe constituée de 5 arcs successifs de sinusoïde,
• de l'effort vocal, en relation linéaire avec l'amplitude pendant l'attaque et la chute de la note seulement: dans le corps de la note, I'effort continue à croître bien que l'amplitude se soit stabilisée.

Dans ce travail on a privilégié la restitution d'un certain type de bruit, la mise en valeur du rôle des harmoniques pairs et impairs, et surtout l'articulation, c'est à dire les consonnes. Dans le programme CHANT, on peut contrôler le bruit des paramètres dépendant des formants, c'est à dire qu'on détermine une amplitude de bruit en rapport avec l'amplitude du formant respectif, et une bande de bruit centré sur la fréquence de ce formant.

Dans cet exemple le bruit a été abordé en travaillant essentiellement sur l'aléatoire, surtout au niveau des micro-fluctuations du fondamental et des fréquences des formants. Pour le timbre, nous avons été amenés à introduire l'idée d'un coefficient d'octaviation, c'est à dire d'un contrôle d'amplitude séparé des harmoniques pairs et impairs, lui aussi affecté d'une enveloppe et d'une variation aléatoire. L'octaviation permet tout un jeu sur la rugosité, déjà induite d'une autre manière dans le fonctionnement de base du programme par un paramètre spécifique, et permet aussi de jouer sur la fusion/fission de l'image auditive (cf. [(S.Mc.Adams]).

L'articulation a été particulièrement travaillée. Des consonnes ont été modélisées et restituées sous forme de transitions d'une voyelle à une autre, affectant l'amplitude, le fondamental, et les trajets formantiques, c'est à dire la fréquence de chaque formant en fonction du temps.

Enfin le rythme et l'accentuation ont été déterminés par des règles décrivant les corrélations entre les durées des phénomènes, et des variations locales de l'effort vocal, de la fréquence fondamentale et du vibrato.

Ceci ne présentait pas de difficulté particulière, une fois la définition d'une transition réalisée, sinon l'extrême lourdeur de l'utilisation, et par conséquent l'inefficacité qui en résulte pour des applications musicales. Ce type de difficultés suggère un traitement particulier que nous allons évoquer.

3.4 Modèles et dérivation

Le propos de ces modèles n'est pas simplement l'imitation ou la simulation d'une note ou d'un instrument donnés dans un contexte donné, mais plutôt de représenter la formalisation d'un acte ou d'un processus quelconque, d'une décision ou d'un geste, d'une organisation statique ou dynamique, ou encore d'un invariant musical en général.

Ces modèles doivent être envisagés comme des structures de connaissances, et bien entendu, ils doivent être utilisés comme tels, c'est à dire qu'ils n'auront de sens pour le compositeur que d'un point de vue référentiel, comme des schémas cognitifs desquels on dérive par modifications ou compositions successives. Ce sont en quelque sorte des propositions au sens quasi logique du terme, et par conséquent le compositeur ne doit pas être obligé d'en voir la structure profonde, il peut se contenter de les manipuler, de les assembler, comme il a toujours fait du reste dans la musique instrumentale ou vocale. Ainsi la compréhension du fonctionnement interne ne doit pas être rendue indispensable mais facultative sans pour autant devenir occulte, et aussi et surtout sans perte de complexité pour l'utilisateur.

On voudra par exemple assembler ces modèles sans avoir à se soucier d'éventuelles incompatibilités de l'un à l'autre, ce qui pose parfois des problèmes insolubles dans certains langages de programmation.

En effet, il ne suffit pas de pouvoir faire en théorie, il faut encore pouvoir le faire simplement, et sans avoir à tout réécrire pour chaque application. Notamment, une transition doit être prise en charge par un objet pré-existant qu'on manipule de manière symbolique, et qu'on place «sur» un autre objet, ou entre deux objets. Ce traitement quasimodulaire ou symbolique, dérive presque automatiquement de la conception de modèles telle que nous l'avons décrite. Ainsi une transition est aussi dans ce sens un modèle, qu'on veut pouvoir placer dans un contexte, sans se préoccuper des questions de compatibilité entre deux ou plusieurs objets.

Une fois le travail spécifique de modélisation accompli, se trouve donc définie la nécessité d'une structure de plus haut niveau pour gérer les modèles, comme autant d'objets dans une combinatoire symbolique, permettant à la fois des modifications réciproques des objets «en situation» dans un contexte, et un contrôle d'encore plus haut niveau sur la combinatoire elle-même.

Ce sont ces impératifs qui nous ont amenés à envisager la réalisation d'un nouveau programme, d'un nouveau langage, pour contrôler CHANT, mais aussi pour contrôler tout autre système de synthèse moyennant une interface réduite et spécifiable dans le programme lui-même. Ce programme, nommé FORMES, dont le développement s'effectue en Lisp, touche directement à des problèmes relevant de l'intelligence Artificielle, notamment les questions de structures de connaissances, de contraintes, de parallélisme et de transformations, c'est à dire les aspects algorithmiques de séquencement de règles aussi bien au niveau horizontal de la succession temporelle, qu'au niveau vertical de l'enchâssement des règles.

Conclusion

La qualité sonore de la synthèse et la facilité d'utilisation du programme en font un outil exceptionnel pour la musique informatique. Depuis sa réalisation il a été utilisé dans une grande variété de contextes musicaux par de nombreux compositeurs, parmi lesquels Gerald Bennett, Connad Cummings, Jean-Baptiste Barrière, Jonathan Harvey, Jukka Tiensuu, Harrison Birtwistle, Kaija Saariaho, Michel Tabachnik, Gerard Grisey, Alejandro Vinao, Tod Machover, Marco Stroppa...

Utilisé en permanence à l'IRCAM, CHANT continue à évoluer, en s'enrichissant des nouvelles utilisations et à travers de nouvelles implémentations sur des machines différentes. La première version de CHANT a été écrite en langage SAIL, par Xavier Rodet et Yves Potard, sur le PDP-10 à l'IRCAM, et a tourné de 1979 à 1983. Une version transportable écrite en FORTRAN fut réalisée en 1981 par Jean Holleville. Au moment du passage du PDP-10 au VAX-780 début 1983 c'est cette même version FORTRAN qui a été entière de sous-programmes de l'utilisateur a été traduite en FORTRAN et en C. Il faut aussi mentionner que CHANT tourne depuis 1981 dans sa version filtres sur la Samson-Box au Computer Center for Reseorch in Music and Acoustics de l'Université de Stanford. La version FORTRAN tourne aussi sur un VAX-750 à l'Electronic Music Studio de Stockholm. En 1983, une version filtres temps-réel de CHANT a été implémentée par Xavier Rodet sur le processeur numérique de sons temps-réel 4X de l'IRCAM.

Enfin, en 1984, Yves Potard a réalisé une nouvelle version de CHANT sur un Array-Processor FPS100. Cette version très rapide permet de combiner la version FOF et la version filtres. De plus la source, au lieu d'être simulée, peut être une source réelle, par exemple un son concret, ce qui autorise alors la possibilité de traitements, voire même de synthèse croisée en combinant les 2 modèles. CHANT est donc devenu aujourd'hui un package complet de synthèse et de traitements.

Bibliographies

BENNETT G. - 1981 «Singing Synthesis in Electronic, Music».In Research Aspects of Singing, ed. J. Sundberg. Publication 33. Stockholm: Royal Swedish Academy of Music, pp.34-50.

CARRÉ R. - 1981. «Couplage conduit vocal - source vocale». In XII^eme Journées d'études sur la parole, Montréal, May, pp.233-245.

FANT G. - 1970 The Acoustic Theory of Speech Production. The Hague: Mouton.

FANT G. - 1973. Speech Sounds and Features. Cambridge, Massachussetts (U.S.A): MIT Press.

HARVEY J - 1981.«Mortuos Plango, Vivos Voco: A Realization at IRCAM». Computer Music Journal 5 (4): 22-24.

HARVEY J. et al.- 1984. «Notes on the Realization of Bhakti». Computer Music Journal 8(3) 74- 78.

McADAMS S. - «The Auditory image: A Metaphor for Physical and Psychological Research on Auditory Organizations». In Cognitive Processes in the Perception of Art, ed. R. Crozier and A. Chapman. Amsterdam North-Holland Publishers. «L'image Auditive: une métaphore pour la Recherche Musicale et psychologique sur l'organisation Auditive» Traduction française Rapport IRCAM n°37. 1985.

MOORER J.A. - 1977 «Signal Processing Aspects of Computer Music : A Survey». Proceedings of the IEEE 65(8): 1108-1137. Reprinted in Computer Music Journal 1(1) 4-37.

RODET X. - 1977 «Analyse du signal vocal dans sa représentation amplitude-temps. Synthèse de la parole par règles». Thèse d'Etat, Université de Paris Vl. Paris.

RODET X. and BENNETT G. - 1980, «Synthèse de la voix chantée par ordinateur». In Conferences des Journées d'études 1980. Paris: Festival International du Son, pp 73-91.

RODET X. and COINTE P. - 1984 «FORMES : composition and Scheduling of Process». Computer Music Journal 8(3): 32-50.

ROTHENBERG J. - 1981.«The Voice Source in Singing». In Research Aspects of Singing, ed. J. Sundberg. Publication 33. Stockholm: Royal Swedish Academy of Music, pp.15-33.

SAARIAHO K. - 1983. «Using the Computer in a Search for New Aspects of Timbre Organization and Composition» Presented at the International Computer Music Conference, October 1983, Rochester, New York.

SUNDBERG J. - 1978 «Synthesis of Singing», Swedish Journal of Musicology 60(1): 107-112

SUNDBERG J. - 1979. «Perception of Singing». Speech Transmission Laboratory Quarterly Progress and Status Report 1 -1979. Stockholm: KTH, pp. 1-48

WEINREICH G. - 1977 «Coupled Piano Strings». Journal of the Acoustical Society of America 62(6) : 1474-1484. Also published in 1979 as «Physics of Piano Strings». Scientific American 240: 117-127.

Discographie

____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .

____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .