Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved.

Nonlinear Oscillator Models of Musical Instrument Excitation

Xavier Rodet

ICMC 92, San José (USA) 1992
Copyright © Ircam - Centre Georges-Pompidou 1992

Introduction

Many physical models of sustained musical instruments have been proposed (strings, brass, reeds, flutes and voice [ACROE 90]). Mathematically, these models are dynamic systems [Khalil 92] which can be described by autonomous retarded functional difference and differential equations such as: (1), x'(t)=f(x(t), x(t-T)), or (2), x(t)=f(h

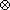x(t-T)), where f is a nonlinear function, T some delay, h a convolution kernel and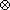

the convolution operator. As an example, the system x' = v and v' = av-bv³-kx has been proposed by Lord Rayleigh [Abraham 82] as a model of clarinet oscillation but we will see below that another model is now preferred.

A standard model of speech production [Ishizaka 72] uses a two-mass model of vocal cords consisting of two coupled Nonlinear Oscillators (NLO) representing a vibrating vocal cord. A one mass model can be described by a nonlinear system: x' = v, v' = g(x,u,v) and u' = (c+ax)[f(x,u,v)-h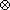u], which has the form of the equations (1) and (2) above without the x(t-T) delayed term. But for strings, reed-woodwinds or brass, the delay term plays an essential role. In some clarinet models the instrument itself is represented by a delay line and the non-linear excitation is represented by a time-varying pressure- or velocity-controlled reflection coefficient. Similarly, a very accurate model of clarinet excitation has been designed at IRCAM. The reed is an NLO driven by mouth pressure and bore pressure. In violin models also (e.g. at CCRMA, ACROE and IRCAM) the string is set into oscillation by the bow and the combination is an NLO. We have also implemented a model for the lips of the trumpet player [Rodet in ACROE 90], where lips are represented by an NLO with two degrees of freedom, moved by pressure from the mouth and mouth piece.

The delay found in the previous instrumental models comes from the instrument itself which is relatively easy to measure or estimate and can be modeled rather accurately as a linear system, by using, for instance, a state-space representation[Depalle 92]. One of the other key points for music synthesis is modeling the excitation process. This is why we present here research on non linear oscillators coupled to passive linear systems as a general model of a large class of musical instruments [McIntyre 83].

A clarinet-like basic model

As an example, we examine the reed of a clarinet-like instrument coupled to the bore. Following [McIntyre 83], let us call qo and qi the outgoing and incoming pressure waves in the bore respectively, p the pressure in the player's mouth and z the characteristic impedance of the bore. The system can be described in a simplified way by the equations: 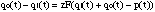, , 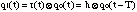where h(t-T)=r(t) is the reflection function of the bore. The most important assumption here is that the reed has no mass, leading to a memoryless nonlinearity F. In the case where this system has a unique solution, then: qo = (h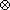qo(t-T)). This is a very simple model to explain the basic oscillatory behavior of the reed in a clarinet-like instrument (Figure 1). To better understand this behavior, [McIntyre 83] and [Magenza 85] note that if h(t) is simplified into a dirac dt (the sign inversion is included in ) then: qo(t)=(qo(t-T)), and similarly for qi. The signal value qo(t) depends only on the value at t-T. If qo(t)=Q0 is constant on [-T, 0] then it is constant on any interval [(n-1)T, nT] with a value: Qn=(Qn-1).

We now examine this iterated map as the basic model of a clarinet like instrument. If p=0, then qo should stay zero. Thus the origin O is a fixed point of the map. In order for the system to oscillate around O, as we expect a musical instrument to do, the slope s1 of a smooth map about O has to be less than -1 (Figure 2). In order for the signal not to grow to infinity, the slope of has to become greater than -1 at some distance from O. Let us first choose as two segments with slopes s1<-1 and s2>-1 for Q>0 and symmetric around O (Figure 2).

Roles of the slopes s1 and s2

It can easily be seen that |s1| controls the transient onset velocity, the greater |s1|, the faster the onset. We have here a clear control parameter for the onset behavior of our instrument. If h(t)=d, the signal is a square wave. If h(t) is a low pass kernel, then the signal is rounded. This can be controlled by |s2|: the closer |s2| to 1, the less high frequencies in qo. This can also be viewed as follows: in the square wave case the system uses only two points of the map and in the rounded case it uses more points spread more regularly on the map.

As a first result, we have found that two important characteristics of the sound, transient onset velocity and richness, are controlled by the slopes s1 and s2. We have been lead to adopt the s1-s2 map by control considerations of the basic clarinet-like instrument. Remarkably, it happens to be the same map as in the Chua's circuit, described for instance in [Matsumoto 85] where different behaviors of this system are examined.

If we want a continuous map, we may choose a simple cubic (x)= ax³+s1x (Figure 3), where a is determined again according to the slopes s1 in O and s2 at the point of abscissa x0 such that: -x0 = ax0³+s1x0.

Periodicity

For musical purposes we expect to have control of the period of the waveform. In the continuous case, [Chow 85] has studied some similar equations in the form: x(t) = f(h(t)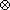x(t-T)). It is shown that under some fairly general conditions on the map f and the kernel h, the period 2 (corresponding to the first mode in a clarinet, i.e. to a period of 2T) is asymptotically stable. This means that we can expect to play and keep some steady tone from the instrument. It is also shown that, if f is symmetrical around O the signal x(t) has the symmetry x(t+T)=-x(t). Then the signal is composed of odd harmonics only. This is an essential characteristic of the clarinet sound. Comparison with other instruments such as trumpet where the nonlinearity is with memory, is under way. In some conditions, periods having durations which are integer fractions of 2T are also possible.

If the slope s2 is greater than 1, the fixed point of the map f²=fdeg.f becomes unstable. We observe period doubling and, for greater values, chaotic behavior. From the sound synthesis point of view, this is very interesting. Period doubling corresponds to subharmonics. In other cases, the signal sounds like noise added to the periodic tone of the instrument but with some relationship between partials and noise. Due to the lack of space, details are differed until the conference.

Conclusion

Using HTM [Freed 92], we have implemented nonlinear oscillators in real time on a SGI Indigo with a Motif-C⁺⁺ graphical-user interface allowing for easy experimentations with their properties and behaviors. We have shown how the excitation of musical instruments can be studied from the point of view of nonlinear oscillators. Among the important results, we look for precise conditions for oscillation, stability, good control parameters and good properties of the generated waveforms. Other basic models of instruments, brass [Rodet 92], voice, flute, and string are studied in the same way as the clarinet, and are compared. We deeply thank the staff of CNMAT where this work has been done. We also thank Profs. L. Chua and S. Sastry for their enthusiastic help.

References

[Ishizaka 72] Synthesis of voiced sounds from a two mass model of vocal chords, K. Ishizaka and J.L.Flanagan, The Bell System Technical Journal, vol 56 N°6, Jul. Aug. 72, pp. 1232-1267.

[Chow 85] Some results on Singular Delay-Differential Equations, S. N. Chow & D. Green Jr., in Chaos, Fractals and Dynamics, edited by , P. Fischer & W. R. Smith, Marcel Dekker, 1983.

[Abraham 82] Dynamics, the goemetry of behavior, R.H. Abraham & C.D. Shaw, Aerial Press 82.

[M.E. McIntyre 83] M.E. McIntyre et al., On the Oscillations of Musical Instruments, JASA 74 (5), Nov. 83.

[Matsumoto 85] The Double Scroll, T. Matsumoto, L.O.Chua and M. Komuro, IEEE trans. Circuits & Syst., CAS-32 (1985) 8, pp 797-818.

[Magenza 89] Excitation non linéaire d'un conduit acoustique cylindrique, Thèse, Université du Maine, France, 85.

[ACROE 90] Proceedings of the Colloquium on Physical Modeling, Grenoble, France, Oct. 1990.

[Depalle 91] P. Depalle, X. Rodet & D. Matignon, State-Space Models for Sound Synthesis, IEEE ASSP Workshop on Appl. of Digital Signal Processing to Audio and Acoustics, Mohonk, New Paltz, New York, Nov. 1991

[Freed 92] Tools for rapid prototyping of Music Sound Synthesis algorithms, A. Freed,Proc ICMC, San Jose, 92.

[Khalil 92] Nonlinear Systems, H.K.Khalil, Macmillan Publishing Company, New York, 1992.

[Rodet 92] A physical model of lips and trumpet, X. Rodet & P. Depalle, in Proc ICMC 92, San Jose, Oct. 1992.