Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved.

Synthesis and Control of Hundreds of Sinusoidal Partials on a Desktop Computer without Custom Hardware

Adrian Freed (CNMAT), Xavier Rodet, Philippe Depalle (IRCAM)

ICSPAT 92, San José (USA), 1992
Copyright © ICSPAT 1992

Introduction

The idea of synthesizing sounds by summing sinusoidal oscillations [Helmholtz 1863] has intrigued generations of musical instrument builders. Thaddeus Cahill's electromechanical implementations [Nicholl 93] illustrate graphically the basic challenge faced by these engineers--the creation of a large number of oscillators with accurate frequency control. Cahill used dynamos constructed from wheels of different sizes attached to rotating shafts ranging in length from 6 to 30 feet. The speed of each shaft was adjusted to obtain the required pitch. A total of 145 alternators were attached to the shafts. Since the vacuum tube and transistor (inventions of this century) were unavailable to Cahill, each rotating element had to produce nearly 12000 to 15000 watts of energy to deliver synthesized music to subscribers' homes.

In the late 1970's, the availability of single chip digital multipliers stimulated the construction of digital signal processors for musical applications [Allen 85]. Although these machines were capable of accurately synthesizing hundreds of sinusoids [DiGiugno 76], their prohibitive cost and limited programming tools precluded widespread use.

One hundred years after Cahill's work, despite rapid gains in computational accuracy and performance, the state of the art in affordable single chip real-time solutions to the problem of additive synthesis offers only 32 oscillators. Since hundreds of sinusoids are required for a single low pitched note of the piano, for example, current single chip solutions fall short by a factor of at least 20. This paper describes a new technique for additive synthesis, FFT^-1, that offers a performance improvement of this order. This technique also provides an efficient method for adding colored noise to sinusoidal partials, which is needed to successfully synthesize speech and the Japanese Shakuhachi flute, for example. Before describing the details of the FFT^-1 method, additive synthesis will be compared to the popular synthesis methods: frequency modulation [Chowning 73] and digital sampling.

Additive synthesis, FM and Digital Sampling

Additive synthesis is a signal modeling approach and therefor inherits a rich history of signal processing techniques including methods to automatically analyze sounds in terms of sinusoidal partials and noise [Garcia 1992, McAulay & Quatieri 1986, Serra 1986]. The image below illustrates the result of such an analysis. It shows analyzed partial trajectories superimposed over successive short term spectra of a tenor voice recording.

Because independent control of every partial is available in additive synthesis, it is possible to implement models of perceptually significant features of sound such as inharmonicity, brightness loudness, and roughness. In commercial digital samplers, sound amplitude and pitch are readily controlled, but no fine control over the sound spectrum is possible for timbre manipulations. Recent products allow for coarse timbral manipulations by voice blending and filtering. However, without fine control over individual elements of the spectrum it is impossible to implement, for example, continuous changes in harmonicity.

Another important advantage of additive synthesis over digital sampling is that it allows the pitch and length of sounds to be varied independently [Quatieri&McAulay 92]. The sample rate conversion technique [Smith&Gossett 84] used in digital samplers achieves pitch alterations by changing the rate at which sounds are read from memory. This results in changes to the durations of those sounds.

Another important aspect of additive synthesis is the simplicity of the mapping of frequency and amplitude parameters into the human perceptual space. These parameters are meaningful and easily understood by musicians. This is in contrast to the parameter space of the frequency modulation synthesis method which maps awkwardly to the spectral domain through Bessel functions [Corrington 1970].

Additive Synthesis by the Oscillator Method

Additive synthesis is usually done with a bank of sinusoidal oscillators. Let J be the number of partials of the signal to be computed at a certain time, namely a sample number n. Let the frequency, the amplitude and the phase of the j^th partial, l<=j<=J, be named respectively fj, aj, and j. More precisely, since they are functions of time, i.e. of n, they are written fj[n], aj[n], and j[n]. Usually, fj[n] and aj[n] are obtained at each sample by linear interpolation of the breakpoint functions which describe the evolution of fj and aj. The phase, commonly ignored, requires careful treatment as discussed later. The j^th partial is defined by:

cj[n] = aj[n]^.cos(j[n])

j[n] = j[n-1] + F(2fj[n],SR)

where SR is the sampling rate and the signal to be computed is:

s[n] = cj[n]

j=1

In the digital oscillator method, commonly used in frequency synthesizers [Tierney et al. 1971], the instantaneous frequency and amplitude are calculated first by interpolation. Then the phase j[n] is computed. A table lookup is used to obtain the sinusoidal value of this phase and the sinusoidal value is multiplied by aj[n]. Finally cj[n] is added to the values of the j-l previously computed partials The computation cost Cadd(J) of the oscillator method is of the form J per sample. Assuming linear amplitude and frequency interpolation, is the cost of at least 4 additions, 1 table lookup, 1 modulo 2ⁿ, and 1 multiplication. The factor varies considerably between processors according to available parallelism. It is interesting to note that with careful pipelining all of the operations involved in the computation of a sample for each oscillator may be performed in parallel and that in current VLSI technology the table lookup operation has the longest latency. Oscillators based on higher order recursions [Smith&Cook 1992] and CORDIC operations [Hu 1992] have been proposed, but implementations have not yet demonstrated significant performance advantages over the direct table lookup oscillator. This is because the cost saving associated with avoiding a table lookup is offset by the additional cost of maintaining and accessing additional state variables, the interaction between frequency and amplitude controls [Gordon&Smith 85], and managing the effects of finite wordlength [Abu-El-Haija&Al-Ibrahim 86].

Additive Synthesis by Inverse Fast Fourier Transform

In the FFT^-1 method [Depalle&Rodet 90], computation of partials is not done by a bank of oscillators but by an Inverse Fast Fourier Transform, a transformation of a short term spectrum (STS) Sl[k] into the corresponding time-domain signal swl[n]. To better explain the method, the STFT analysis method [Nawab&Quatieri 1988] is reviewed in which a signal s[n] is first partitioned into successive overlapping frames sl[m].

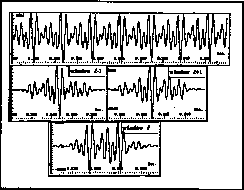
Each frame is multiplied by a window signal w[m]. Note that with an appropriate choice of w and of the overlapping factor d (typically d=0.5), s[n] can be exactly reconstructed from the windowed frames swl[m] by the overlap-add method. The complex STS of each windowed frame is then computed by FFT, leading to a succession of spectra S0[k], Sl[k], S2[k], ... etc. The FFT^-l method is simply the inverse process. First the spectra Sl[k] are constructed, their Inverse Fourier Transforms are computed to obtain the swl[m] and finally the swl[m] are windowed and added with overlap to create the time-domain signal s[n].

Any signal can be exactly constructed in this manner, provided that exact successive spectra Sl[k] are computed and given to the inverse transform. For reasons of efficiency however some approximations are required. First, as shown in the STS magnitude below, a partial is represented in a spectrum by a few points of significant magnitude, typically K=9.

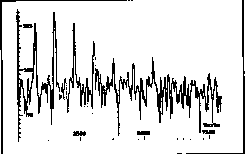
This means that to build the contribution of a given partial in the STS Sl[k], K spectral values need to be computed and added to Sl[k]. If N is the size of a frame (typically N=256), this results in a gain in computation efficiency roughly proportional to N.d/K = 14. A second approximation is that if the parameters of a partial are slowly varying they may be considered constant during one frame, i.e. a pure sinusoid during the small interval of one frame. The advantage of this optional approximation is that the time-domain function is symmetric implying asa real spectrum. As explained later, this replaces a complex multiplication (implemented as 4 real multiply and 2 real add instructions) by 2 real ones. However, this advantage is balanced by some drawbacks. Since the window w has to be symmetrical, fast changes in amplitude or frequency require short windows, thereby decreasing the computational saving of the method. This tradeoff can be adjusted according to the application, and the processor in use. Also a dynamic adjustment according to the rates of changes in amplitude or frequency is conceivable.

Details of Construction of a STS

Let fj, aj and j be the mean values of fj[n], aj[n], and j[n] on the frame l. Let W be the Fourier Transform of the window w. Then the contribution of the partial j in the STS Sl[k] is aj^.e^ij.W[fj/SR-k], which means that W is shifted in order to be centered around fj and multiplied by the complex amplitude aj^.e^ij. Naturally this complex contribution is added in Sl[k] to the contributions of the other partials. Note that, as mentioned in the previous section, a complex-complex or real-complex multiply is required between aj^.e^ij and W[fj/SR-k] according to whether W is complex or real.

Optimizations

The computation of the inverse FFT has a fixed cost, independent of the number of spectral components. It amounts to a small fraction of the performance of modern processors. For example at a sample rate of 44.1Khz the computation of a 256 point real inverse FFT for every 128 output samples accounts for only 10% of the computational capability of the MIPS R4000 processor of the SGI Indigo workstation. In contrast to the FFT, the cost of the construction of a STS is proportional to the number J of components and must be minimized. This cost decreases with the number K most significant values in the spectrum W of the window. For this reason a good window has few significant values. But for an exact construction of signals, the sum of two overlapped windows is required to be exactly 1 in the overlapped region. Moreover, in this region the amplitudes and the frequencies of the partials should be interpolated by the windows from the value in one frame to the value in the next frame. This second, amplitude interpolation requirement suggests a triangular window which is not compatible with the first requirement. There is a simple way out of this dilemma: two windows -- one in the frequency domain to satisfy the first requirement and the other in the time domain. The first window wl has as few significant values as possible and is used to compute the contribution of each partial to the STS Sl[k] as explained earlier. Then the result of the inverse transform of Sl[k] is the time domain windowed frame wl[m].s[m] where s[m] is the desired output signal. Then a second window w2 is applied. It is defined by w2[m]=tr[m]/wl[m], where tr[m] is the triangular symmetric window. The result of this application is:

w1[m].s[m].tr[m]/w1[m] = s[m] .tr[m],

fulfilling the second requirement of a triangular window on the time-domain signal. Note that this procedure is not costly since it is applied globally for all the partials after the inverse FFT. But it insures that the overlap-add uses frames of signal with a triangular window, s[m].tr[m]. The advantage of this procedure is that amplitudes of partials are linearly interpolated as in the classical oscillator method. Moreover, by an adequate phase adjustment (discussed in the next section), this procedure allows for removal of a great deal of the amplitude modulation distortion which may appear when the frequency of a partial varies rapidly from one frame to the next.

Phase adjustment

To avoid confusion, superscripts l and l+1 will be used for to index successive frames: let f^l, a^land f^l+l, a^l+1 be the frequency and amplitude of a partial in these frames. When f^l != f^l+lsome amplitude modulation can occur by phase cancellation in the overlapped region as shown below.

This modulation is maximal at the point where the two triangular windowed overlapped sinusoids are of equal amplitude. The corresponding instant is easy to find because the window w2 is triangular and hence linear. The modulation can be significantly reduced if the phase function in each frame is chosen so as to be equal at time . Naturally the chosen value is the phase determined by a higher level control structure implementing a model of time varying frequency and amplitude.

Noise components

With the FFT^-l synthesis method, noise components can be precisely introduced in any narrow or wide frequency band and with any amplitude. Bands of STS's of wl windowed noise are added to the STS under construction. This is simple and inexpensive when the noise STFT is precomputed and stored in a table before the beginning of synthesis.

Implementation and Performance

The FFT^-1 algorithm has been implemented using a signal processing vector library UDI [Depalle & Rodet, 1990] and in real time on the array processor of the SUN-Mercury Workstation [Eckel et al. 1987] and on the MIPS RISC processor of the SGI Indigo [Freed 1992]. In terms of cost, one of the critical elements is the construction of a STS Sl. Each partial requires K iterations of the form:

aj^.e^ij.W[fj/SR-k] for k [, ]

= j-F(k-1,2), = j+F(k-1,2)

with

j = F(fj,SR.q)

where

q is the oversampling factor

For efficiency, W is oversampled and tabulated. Let Wj,k represent a real value from the table W.

The complex value aj^.e^ij is computed outside the loop K as aj^.e^ij = x + i y. The instructions in the loop are then:

* read Wj,k from the next location in the table W

* compute x*Wj,k and y*Wj,k

* add x*Wj,k and y*Wj,k to the next locations of the complex STS Sl.

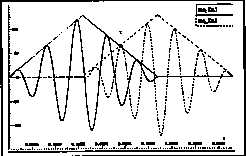
By careful coding, many of the performance enhancing features of modern processors [Hennessey & Patterson 90, Lee 88] may be used to efficiently implement this critical inner loop. The SGI Indigo implementation takes advantage of the ability of the R4000 to overlap the execution of integer address operations, floating point additions and multiplications, delayed writes and multiple operand fetches into cache lines. It is interesting that the table for the oversampled window W is small enough to fit into on-chip data caches of modern processors. This is not the case for the larger sinusoid table required in standard oscillator based additive synthesis. The following graph compares the performance of additive synthesis by oscillator and by FFT^-1.

Control by Spectral Envelopes

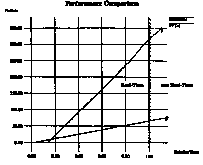
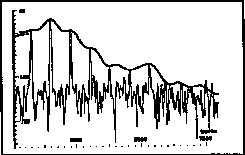
Amplitude Spectral Envelope of a STS

In common implementations of additive synthesis, fj[n] and aj[n] are obtained at each sample by linear interpolation of breakpoint functions of time which describe the evolution of fj and aj versus time. When the number of partials is large, control by the user of each individual breakpoint function becomes impractical. Another argument against such breakpoint functions follows. For voice and certain musical instruments, a source-filter model [Rodet et al. 87] captures most of the important behavior of the partials. In these models the amplitude of a component is a function of its frequency, i.e. the transfer function of the filter [Rodet et al. 86]. That is, the amplitude aj can be obtained automatically by evaluating a spectral function called the spectral envelope e(fj) at the frequency fj of the partial j. The amplitude variations induced by frequency variations may be very large [Rodet et al. 86]. In consequence, a breakpoint function of time cannot neglect these amplitude variations and therefor needs many breakpoints. Moreover, the amplitude of a partial is then not an intrinsic property of the sound independent of other characteristics such as the fundamental frequency. Encoding amplitude as breakpoint functions of time precludes modifications of fundamental frequency or vibrato.

On the other hand, a spectral envelope can be described as an analytical function of a few parameters, independent of the number of partials. It can vary with some of its parameters for effects such as transitions between formants and spectral tilt or spectral centroid changes known to be related to perceptual parameters such as loudness and brightness [Wessel 79] and vocal effort [Sundberg 87]. Also, spectral envelopes are effective for the description of noise components. Spectral envelopes can be obtained automatically by different methods, for example, Linear Prediction analysis [Rodet&Depalle 86]. If the amplitudes and frequencies of the partials are already known from sinusoidal analysis, the Generalized Discrete Cepstral analysis [Galas&Rodet 90, 91] provides reliable envelopes, the smoothness of which can be adjusted according to an order parameter as in classical cepstral analysis. The previous arguments motivate the decision to represent amplitudes of partials by use of successive spectral envelopes defined at specific instants, for example the beginning and the end of the attack, sustain and decay of a note, etc....[Rodet et al. 88]. Then at any instant the spectral envelope to be used is obtained by interpolation between two successive envelopes. These specific instants may be found automatically for the optimal reconstruction of the sound by linear interpolation between two successive envelopes [Montacié].

Frequencies and phases also can be described by similar generalized spectral envelopes. As an example, sustained sounds have partials with frequencies very close to harmonic values of the fundamental frequency. It is therefore computationally advantageous to record only the deviation from harmonicity as a function, called the frequency deviation envelope, of the harmonic number or of the harmonic frequency. Then, at the synthesis stage, it is easy to compute the frequency of a partial, retaining control of the amount of inharmonicity in the resulting sound. The same procedure can be applied for the phases of the partials.

Conclusion

The new method of additive synthesis by FFT^-1 brings a solution to the three main difficulties of classical additive synthesis: efficiency, noise, and control.

Processing time (calculation cost) is an order of magnitude less than that required for oscillator-based additive synthesis. Apart from one inverse FFT - the cost of which is independent of the number of voices and of sinusoid and noise components - the calculation is reduced to the construction of the Short Term Spectrum. By optimization in time and frequency domains this construction may be reduced, for each sinusoid, to simple table lookups and multiplications of a small number of values. As in the case of oscillator-based additive synthesis, this procedure can build sinusoids with rapidly-varying amplitude and frequency, and with phase control if required.

Noise of arbitrary amplitude and bandwidth can be precisely and easily added to the short term spectrum. Automatic methods for analyzing sounds in terms of partials and noise can be easily applied to FFT^-l synthesis.

Control of additive synthesis is made easier by use of spectral envelopes instead of the time-domain breakpoint functions traditionally used for additive synthesis. Properties of desired sounds are expressed in terms of features such as the amplitude envelope of partials, fundamental frequency, deviation from harmonicity, noise components, etc. These spectral envelopes need only be defined at a small number of specific times such as the beginning of an attack, the end of attack, the end of sustain, etc.... Then at any time, the synthesis algorithm uses envelopes interpolated between the defined envelopes. This procedure yields economical and efficient user control.

Several years of experimentation with the FFT^-1 method demonstrate that the method provides good control over a wide range of sounds of high quality. Experience with implementations on affordable desktop workstations suggest that a low-cost real-time multi-timbral instrument based on FFT^-l is within reach. It would have all the possibilities of present day synthesizers, plus many others such as the precise modifications of recorded sounds, speech and singing voice synthesis.

Acknowledgments

The authors gratefully acknowledge the support of Gibson, Silicon Graphics and Zeta music. Alan Peevers provided the 3 dimensional analysis plot.

References

A. I. Abu-El-Haija & M. M. Al-Ibrahim, "Improving Performance of Digital Sinusoidal Oscillators By Means of Error Feedback Circuits,":, IEEE Trans. on Circuits and Systems, Vol. cas 33, no. 4, April 1986.

J. Allen, "Computer architectures for digital signal processing," Proc. of the IEEE 73(5), 1985.

J. Chowning, "The synthesis of complex audio spectra by means of frequency modulation", Journal of the Audio Engineering Society 21:526-534, 1973.

M. S. Corrington, "Variation of Bandwidth with Modulation Index in Frequency Modulation," Selected Papers on Frequency Modulation, edited by Klapper, Dover, 1970

P. Depalle & X. Rodet, "Synthèse additive par FTT inverse", Rapport Interne IRCAM, Paris 1990.

P. Depalle & X. Rodet, "UDI, a Unified DSP Interface for Sound Signals Analysis and Synthesis", Proc. Comp. Music Conf., 1990, Computer Music Association.

G. DiGiugno, "A 256 Digital Oscillator Bank," Presented at the 1976 Computer Music Conference, Cambridge, Massachusetts: M.I.T., 1976

G. Eckel, X. Rodet and Y. Potard, "A SUN-Mercury Workstation", ICMC, Urbana, Champaign, USA, August 1987.

A. Freed, "Tools for Rapid Prototyping of Music Sound Synthesis Algorithms and Control Strategies", in: Proc. Int. Comp. Music. Conf., San Jose, CA, USA, Oct. 1992

T. Galas & X. Rodet, "An Improved Cepstral Method for Deconvolution of Source Filter Systems with Discrete Spectra", Int. Computer Music Conf., Glasgow, U.K., Sept. 90.

T. Galas & X. Rodet, "Generalized Discrete Cepstral Estimation of Sound Signals" IEEE Workshop on Application of Signal Processing to Audio and Acoustics, Oct. 1991.

G. Garcia, "Analyse des signaux sonores en termes de partiels et de bruit. Extraction automatique des trajets fréquentiels par des Modèles de Markov Cachés," Memoire de DEA en Automatique et Traitement du Signal, Orsay, 1992

H. L. F. von Helmholtz, "On the Sensations of Tone as a Physiological Basis for the Theory of Music", 1863, Translation of the 1877 Edition, Dover, 1954

J. W. Gordon & J. O. Smith, "A Sine Generation Algorithm for VLSI Applications," Proc. of ICMC 1985, Computer Music Association

J. L. Hennessey and D. A. Patterson, 1990, "Computer Architecture: A Quantitative Approach", Morgan Kaufmann, Palo Alto, CA.

Yu Hen Hu, "CORDIC-Based VLSI Architectures for Digital Signal Processing," IEEE Signal Processing Magazine, July 1992.

J. Laroche and X. Rodet, "A new Analysis/Synthesis system of musical signals using Prony's method", Proc. ICMC, Ohio, Nov. 1989.

E. A. Lee, "Programmable DSP Architectures", IEEE ASSP Magazine, October 1988

R.J. Mc Aulay and Th. F. Quatieri, "Speech analysis/synthesis based on a sinusoidal representation", IEEE Trans. on Acoust., Speech and Signal Proc., vol ASSP-34, pp. 744-754, 1986.

C. Montacié, "Décodage Acoustico-Phonetique: apport de la décomposition Temporelle Géneralisée et de transformations spectrales non-linéaires", These de l'URA 820, Telecom-Paris, Paris 1991

S. H. Nawab and Th. F. Quatieri, "Short-Time Fourier Transform" in Advanced Topics in Signal Processing, J. S. Lim, A. V. Oppenheim Editors, Prentice-Hall, 1988

M. Nicholl, "Good Vibrations", Invention and Technology, Spring 1993, American Heritage.

Th. F. Quatieri and R. J. McAulay, "Shape Invariant Time-Scale and Pitch Modification of Speech", IEEE Trans. on Signal Processing, Vol. 40 No. 3, March 1992.

X. Rodet, "Analysis and Synthesis Models for Musical Applications", IEEE Workshop on application of digital signal processing to audio and acoustics, Oct. 1989, New Paltz, New-York, USA.

X. Rodet, Y. Potard, J.B.B. Barrière, "The CHANT Project", Computer Music Journal, MIT Press, fall 85.

X. Rodet, P. Depalle, "Use of LPC Spectral Estimation for Analysis, Processing and Synthesis", 1986 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New-Paltz, New York, September 1986

X. Rodet, P. Depalle & G. Poirot, "Speech Analysis and Synthesis Methods Based on Spectral Envelopes and Voiced/Unvoiced Functions", European Conference on Speech Tech., Edinburgh, U.K., Sept. 87.

X. Rodet, P. Depalle & G. Poirot, "Diphone Sound Synthesis", Int. Computer Music Conf., Köln, RFA, Sept 88.

X. Serra, "A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition", PhD dissertation, Stanford Univ., 1986.

J. O. Smith and P. R. Cook, "The Second-Order Digital Waveguide Oscillator," Proc. ICMC, Computer Music Association, 1992.

J.O. Smith and P. Gossett, "A Flexible Sampling-Rate Conversion Method," Proc. IEEE ICASSP, vol. 2 , pp. 19.4.1-19.4.2, San Diego, March 1984.

J. Sundberg, "The Science of Singing," DeKalb: Northern Illinois University Press, 1987.

J. Tierney, C. M. Rader, and B. Gold, "A digital frequency synthesizer," IEEE Trans. Audio Electroacoustics, vol AU-19, pp 48-57, March 1971.

D. Wessel, "Timbre space as a musical control structure," Computer Music Journal 3(2):45-32, 1979.