
 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved. |
Stability/Instability of Periodic Solutions and Chaos in Physical Models of Musical Instruments
Xavier Rodet
ICMC 94, Aarhus (Danemark) 1994
Copyright © Ircam - Centre Georges-Pompidou 1994
Abstract
We study multiple solutions and chaos in simple physical models and their stabilities.
A path toward a unique
solution can be based upon the low pass character of the linear element. Chaotic signals
are shown to cover a large space ranging from a sound perceived as harmonic without
noise up to an essentially noisy sound. This is a very important feature for sound
synthesis since the synthesis of noise and irregularities of traditional instruments
has always been difficult and unsatisfactory. Methods are proposed to find the solutions
and their stabilities, and to obtain controllable systems with periodic and chaotic behaviors.
1. Introduction
Real instruments and computer simulations, usually called physical models, often have
more than one oscillating solution for a given setting of their parameters [Valimaki
et al. 93], [Idogawa 92], [Rodet 93c]. On one hand, it can be argued that this is
part of the richness of a musical instrument. On the other hand, unpredictable solutions
can render the usage of a physical model rather difficult in a real-time musical
performance. Only stable solutions should be considered because unstable ones do
not persist. Therefore, the first goal of this paper is to study the multiple solutions of
simple physical models and their stabilities. We explain that a path toward such
a goal could eventually be based upon the low pass character of the linear element.
As a second goal, it would be an interesting achievement to design a system which would model
the usual playing behavior of an instrument but could avoid the other behaviors if
requested. By the other behaviors, we mean those corresponding to stable solutions
other than the usual playing solution.
Finally, our last goal is to control the ratio of non sinusoidal components (noise)
induced by chaos in synthetic signals, opening a new field of fascinating research
and applications. Many systems which have been used as models of physical instruments
for music synthesis can produce chaotic signals in some regions of their parameter space.
This is related to instability since chaos often appears when all periodic solutions
become unstable. The most innovative direction is probably in the area of the control of chaotic behavior of the models and thus of chaotic sounds. In the past it may
have seemed that chaotic sounds could not be of any musical interest. To our great
surprise we have found the contrary: these signals exhibit very interesting properties,
such as a clearly perceived pitch or an intermittent type behavior. We have also found
that a signal which is mathematically chaotic can be perceived in a very different
way. Actually, chaos can happen within a more or less small neighborhood of a periodic
trajectory. It can cover a large space, from a
sound perceived as harmonic without noise, up to an
essentially noisy sound. This is a very important feature for sound synthesis since
the introduction in synthesis of noise and irregularities of natural instruments
has always been difficult and unsatisfactory. Our models, by themselves, effectively
generate a noise component that is so important for the sound quality of musical instruments.
In more general terms it appears that one should not merely "build" models and deliver
them to musicians. It is indispensable to go into the understanding of the models,
to conceive abstractions of them and to propose explanations helpful to the users.
In particular, this comprehension is indispensable for elaborating the control of synthesis
models, which are at the same time efficient and musically pertinent.
2. Uniqueness of solutions and low pass feedback loop
We have mentioned in the introduction our interest
for the design of a system which would model the usual playing behavior of an instrument
but could avoid the other behaviors if requested. For the feedback systems studied
here it is conceivable that a path toward such a goal could be based upon the low
pass character of the linear element. In [Bergen 71], the low pass character above the
oscillation frequency appears among the sufficient conditions for oscillation according
to the describing function method. However it does not guarantee the uniqueness of
the solution. The low pass character appears also in the formulation of the Hopf theorem
in the frequency domain [Mees 79],
[Rodet 93c] which gives sufficient conditions for oscillation and uniqueness of the
solution.
Similarly, the linear part of Chua's circuit [Chua 90], at least for some values of
the parameters, can be viewed as a band pass filter, i.e. a low-pass filter above
the frequency of a pair of conjugate poles, this frequency being approximately the
oscillation frequency. This suggests some relation with the dominant mode of an acoustic
instrument [Rodet 93b]. This idea has also been evoked in [Wawrzynek 83] but was
not fully developed. It can be shown [Rodet 93e] that there is a precise correspondence
between Chua's circuit and a model of an acoustic instrument where the feedback loop is
limited to the first mode(s) (the first mode could easily be replaced here by
the dominant
mode in the same way). Naturally, the system so
obtained has a unique oscillatory solution in a certain range of parameter values.
Fig. 1 shows a possible implementation and the control of each partial through a
second order section.
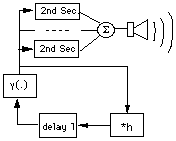
Fig. 1. Feedback loop limited to the first mode(s).
3. NLO systems with chaotic behavior
Many systems which have been used as models
of physical instruments for music synthesis can produce chaotic signals in some regions
of their parameter space. Chua's circuit [Chua 90] is a very simple circuit which
exhibits a surprisingly large variety of bifurcations and chaos. As mentioned in [Madan 92] and [Rodet 92a], signals with period-1, period-2, etc...,
can be obtained and lead to harmonic
sounds. In the case of chaotic signals that can be obtained with some other values,
the corresponding sound can be qualified as noisy
. Some short-time spectra of periodic and chaotic signals from Chua's circuit are
shown in [Rodet 93b]. For certain parameter values noisy signals are obtained together
with some harmonic sinusoidal components.
Some properties and musical uses of the Time Delayed Chua's circuit [Sharkovsky 93]
have been presented in [Rodet 92c] and [Rodet 93d]. Compared to the original Chua's
circuit, the time delayed version includes a delay line which is directly related
to the structure and physics of many classical musical instruments. This delay allows for
much better control of the circuit in terms of musical usage. The delay can also
be seen as a stabilizing feedback loop applied to the original circuit. The Time
Delayed Chua's Circuit exhibits a very interesting variety of sounds which we have analysed
in [Rodet 93c]. This is due to the combination of the rich dynamics of the nonlinear
map together with the number of states represented by the delay line. In particular,
Sharkovsky et al. [1993] have shown a remarkable period-adding property. In some regions
the system has a stable limit cycle with periods 2, 3, 4, etc.... In between every
two consecutive stable regions the system exhibits a chaotic behavior. We also observe the simultaneous presence of sinusoidal components and noise in the signal. By a
proper affine change of variables, the invariant interval of the nonlinear function
used in the circuit can be set to the interval [0,1]. For certain parameter values,
the function is composed of two segments only in the invariant interval [Rodet 93a] with slopes
l1 and l2. When l1 = 1.025 and l2 is varied from 1 to 2 and then to 40, we observe the progressive appearance of non
sinusoidal components superimposed on the harmonic sinusoidal components (Fig. 2).
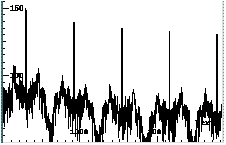
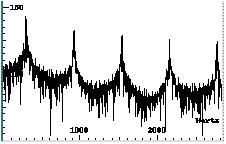
Fig. 2. Spectra showing presence of sinusoidal
components and noise, l2 = 1.7 (top) and 30 (bottom).
This property is very promising since it opens the
possibility of a precise control of the proportion of noise added to the harmonic
components, which is essential for a musical usage. This is the typical property
that we want to extend to nonlinear functions and systems beyond the very specific
two segment function of Sharkovsky 's case.
We focus here on the class of systems composed of an instantaneous nonlinearity and
a linear feedback loop, which is a valid basic
model of reed instruments when the mass of the reed is considered negligible. But
in the case of the trumpet [Rodet 92b] for example, this assumption cannot be maintained:
as we noticed in [Rodet 93c], the clarinet and trumpet would then be represented
by the same model. On the contrary, in [Rodet & Steinecke 94a] we propose a minimal
one mass model of the trumpet in the form of a two-loop system. This system can also
exhibit chaotic behaviors.
For speech production, various models have been proposed. The most common is a two mass model of vocal folds
[Flanagan 72]. Using the impedance of the opening in the glottis and the driving
point impedance of the vocal tract, air flow pressure and velocity in the glottis
are computed and used to drive two coupled non-linear oscillators representing a
vibrating vocal fold. This model usually exhibits bifurcations and chaos often related to the
desynchronisation of lower order modes, e.g. of lateral and vertical motion, or to
a left-right asymmetry [Steinecke & Herzel 93], [Rodet & Steinecke 94b].
4. Stability of 2-periodic solutions of a
class of systems
We consider the following equations which
xn = h * g(xn-T) (1), or xn = g(h * xn-T) (2),
where h is the impulse response of a filter in the linear feedback loop, * is the
convolution operator and g(.) is the nonlinear function representing for instance the influence of the reed
in a basic clarinet model [Rodet 92a]. The system can be decomposed into an instantaneous
nonlinearity g(.) and a linear element including h and a delay. This defines the class of single
feedback loop systems with an instantaneous nonlinearity of which we can easily determine
the stability and some oscillation properties [Rodet 93c]. Note that the only restriction on the linear element is that its impulse response be stable
. In particular the continuous transfer function of the linear element does not need
to be a rational function and thus can include delays. Many systems can be redesigned
to fall into this class. Equation (1) can also be written:
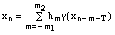 (3)
(3)
(3) defines a map Q:Rm2+T+1 Æ Rm2+T+1. Since we are dealing with physical systems, it is natural to suppose that {hm} is causal, m1 < T and finite and m2 < . The sample n depends on the past samples n-m2-T to n+m1-T. Therefore the set of samples from n-m2 to n+T-1 depends only on the values xn-m2-T to xn+m1-1, themselves depending on the values xn-m2-T to xn-1 only which defines the map Q. Such a system may have many periodic solutions. Since
they are the most important for the normal playing conditions of a musical instrument,
we study here only 2-periodic solutions, i.e. fixed points of Y=Q Q with period length about 2T. But finding the 2-periodic solutions of Q and their
stabilities in general is not easy. Therefore we are going to introduce another system.
Let {sn} be a 2-periodic solution of (3). Assume now that {hn} is even symmetric. We have noticed in [Rodet 93c] that in this case the period 2
is of length 2T exactly, i.e. such that sn = sn+2T for all integer n. Let us take the Fourier series of one period of sn and of g(sn) and call S={Sk} and G(S)={Gk(S)} respectively their Fourier coefficients which are vectors of length 2T. Then
for {sn} equation (3) can be written:
Sk = (-1)k Hk Gk(S) (4),
where the term (-1)k accounts for the time delay T in (3), and H={Hk} is the Fourier series taken after time aliasing of {hn} on an interval of length 2T and overlap-adding.
From equation (4) we define a map M:B2T Æ B2T where B 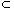 C is the set of Fourier series of real periodic discrete signals of period length
2T:
C is the set of Fourier series of real periodic discrete signals of period length
2T:
Mk(S) = (-1)k Hk Gk(S), k=1,2,...2T (5)
where Gk(S) is the kth Fourier coefficient of g(s) when s is the inverse Fourier series of S. In the time domain, we call P:R2T Æ R2T the map associated with M and defined by:
P(s)=Fourier-1(M(S)) (6)
where Fourier-1
designates the inverse Fourier series, or equivalently:
P(s)=h g(s-T) (7),
where h=Fourier-1(Hk) and is the circular convolution. The reason for introducing the maps M and P is that
they have the same fixed points as Y=Q Q. They are simpler than Y in the sense that they have smaller dimension and that they map exactly the signal
of one time interval of length 2T into the signal of the next time interval. The
dynamical system that they define is different from the original one and we call
it the period-after-period
(p.a.p.) system as opposed to the original one (1). Let DYx be the derivative of Y at the point x 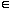 Rm2+T+1. The stability of a fixed point s of Y is given by the eigenvalues of DYs. The problem is therefore to find all the fixed points of Y or equivalently of P and M.
Rm2+T+1. The stability of a fixed point s of Y is given by the eigenvalues of DYs. The problem is therefore to find all the fixed points of Y or equivalently of P and M.
5. Case of a polynomial nonlinearity
The case where g is a polynomial has interesting properties. The first one is that it is easy to implement
and can be efficiently computed on a digital processor. The control of the important
characteristics of g is easy. The slope of g at a fixed point, assumed to be at the origin, controls the oscillating/non oscillating
behavior of the system [Rodet 93b]. This slope is easily changed by a modification
of the linear term of the polynomial. Another property is that the equation (1) or
(2) leads to a system of m2+T-1 polynomial equations in m2+T-1 variables, and that the map P becomes a system of 2T polynomials in 2T variables.
But this is also true for the map M associated with P in the Fourier domain: Note
first that the Fourier series of x2, x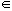 R2T, is the circular convolution X X which is a polynomial in the variables {Xk, k=1,2,...2T}. Then Gk(X) is also a polynomial in the same variables and (5) for k=1,2,...2T defines a system
of 2T polynomial equations.
R2T, is the circular convolution X X which is a polynomial in the variables {Xk, k=1,2,...2T}. Then Gk(X) is also a polynomial in the same variables and (5) for k=1,2,...2T defines a system
of 2T polynomial equations.
The portion of g which we are interested in for easy control of oscillations is that of negative slope
around the origin and greater slope further from the origin [Rodet 92a]. A drawback
of the choice of a polynomial g is that it is not possible to avoid the existence of other points of functioning
than the origin, which is a serious inconvenience for musical usage [Rodet 93d].
We will see in section 10 that a rational function allows us to avoid that difficulty
and can be studied with the same tools which we are using for the polynomials.
6. Solutions of the p.a.p. system: a homotopy method
In general, it is possible to find the solutions of a system of polynomial equations
by a homotopy method [Chow 79]. For two maps M0 and M1:R2T Æ R2T, a homotopy is a smooth map F:R2T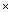 [0,1] Æ R2T, such that F(., 0) is M0(.) and F(., 1) is M1(.). More precisely, we are looking for the zeros of the system of polynomials M1(s)=s-P P(s). Suppose that M0(s) has known zeros, then under certain conditions, it is possible to follow the trajectories
of the zeros of F(s, r) starting from the zeros of M0(s) and going to those of M1(s) when r is varied from 0 to 1. However this is possible provided that no such zero escape
to infinity for some value of r in the interval [0,1] and that 0 is a regular value of F on R2T
[0,1] Æ R2T, such that F(., 0) is M0(.) and F(., 1) is M1(.). More precisely, we are looking for the zeros of the system of polynomials M1(s)=s-P P(s). Suppose that M0(s) has known zeros, then under certain conditions, it is possible to follow the trajectories
of the zeros of F(s, r) starting from the zeros of M0(s) and going to those of M1(s) when r is varied from 0 to 1. However this is possible provided that no such zero escape
to infinity for some value of r in the interval [0,1] and that 0 is a regular value of F on R2T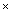 [0,1].The first requirement is easily fulfilled by making sure that the coefficients
of the highest terms of F in sn do not vanish. The second requirement guarantees that F-1(0) is a submanifold of dimension 1, i.e. consists only of arcs from a zero of M0(s) to a zero of M1(s), but it may not be fulfilled for some trajectories in our case. In our problem,
an interesting choice for M0 is the one for which, in the equation (3), h0 = 1 and hm=0 for m 0, M0(s)=s-g g(s), i.e. there is no filtering in the feedback loop. For simplicity we assume from
now on that g(.) is odd symmetric. Let W be the set of solutions of:
[0,1].The first requirement is easily fulfilled by making sure that the coefficients
of the highest terms of F in sn do not vanish. The second requirement guarantees that F-1(0) is a submanifold of dimension 1, i.e. consists only of arcs from a zero of M0(s) to a zero of M1(s), but it may not be fulfilled for some trajectories in our case. In our problem,
an interesting choice for M0 is the one for which, in the equation (3), h0 = 1 and hm=0 for m 0, M0(s)=s-g g(s), i.e. there is no filtering in the feedback loop. For simplicity we assume from
now on that g(.) is odd symmetric. Let W be the set of solutions of:
g(u)= -u, u 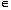 R. (8)
R. (8)
Among the solutions of M0(s)=s-g g(s)=0, s 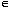 R2T, we retain only the vectors s such that sn
R2T, we retain only the vectors s such that sn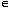 W for n=1,2, , 2T. The other solutions imply a value x
W for n=1,2, , 2T. The other solutions imply a value x 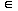 R, x 0, such that g(x)=x which we want to avoid since it corresponds to non-zero fixed points of the
original system, which give no sound. Note that for the solutions which we retain
sn= - sn-T for n=T+1,T+2, 2T. When a signal sn has this odd symmetry of the period with respect to its middle, we say that the signal
is odd harmonic
(o.h.) because its even harmonics are null. The initial solutions for the homotopy
are easy to build since they are the combinations of values from W. Another reason for this choice of M0 is as follows. The homotopy can simply be chosen as:
R, x 0, such that g(x)=x which we want to avoid since it corresponds to non-zero fixed points of the
original system, which give no sound. Note that for the solutions which we retain
sn= - sn-T for n=T+1,T+2, 2T. When a signal sn has this odd symmetry of the period with respect to its middle, we say that the signal
is odd harmonic
(o.h.) because its even harmonics are null. The initial solutions for the homotopy
are easy to build since they are the combinations of values from W. Another reason for this choice of M0 is as follows. The homotopy can simply be chosen as:
F(s, r) = (1-r)M0(s) + rM1(s). (9)
Therefore, when varying r from 0 to 1, we follow the evolution of the solutions according to the increase of
low-pass filtering in the feedback loop, which is one of the main goals we mentioned
earlier.
7. Example of the homotopy method
Let us detail the application of the method on a very simple example. Let T=3 and
g(x)=x3+a1x for a1 = 1.1. We also choose the most simple low-pass filter, h-1=h1=0.25, h0=1-2h1, otherwise hm=0. More precisely, this means that when the homotopy variable r goes from 0 to 1, (h0, h1) goes from (1, 0.), i.e. no filtering, to (0.5, 0.25), progressively applying more
and more low-pass filtering. The solutions of x3+a1x= - x are {0, 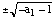 }=W. The initial solutions which we retain for the homotopy are obtained as the o.h.
signals with sample values in W, so that s - g g(s)=0. Two solutions are equivalent if they are identical by sign inversion or time
delay. Then, apart from the identically null solution which is irrelevant, there
are only 5 equivalence classes of solutions. These are shown in Fig. 3 and are designated
by the letters A
, B
, C
, D
, and E
.
}=W. The initial solutions which we retain for the homotopy are obtained as the o.h.
signals with sample values in W, so that s - g g(s)=0. Two solutions are equivalent if they are identical by sign inversion or time
delay. Then, apart from the identically null solution which is irrelevant, there
are only 5 equivalence classes of solutions. These are shown in Fig. 3 and are designated
by the letters A
, B
, C
, D
, and E
.
Starting from one of these initial solutions and from r=0, we increase r by a small Dr, estimate the new solution by the Newton method from the previous solution and iterate
this procedure until r=1. Using prefixed superscripts to index successive steps of the algorithm, let 0s be the initial solution, rs the solution estimated for the value r of the homotopy variable. The solution r+Drs is obtained as follows. Let z0=rs be the initial value for the Newton method, and DF the differential of F. We iterate:
zk+1 = zk - [DF(zk, r+Dr)]-1F(zk, r+Dr), (10)
until when zk+1 - zk is sufficiently small. Then r+Drs gets the last value zk+1. It is easy to derive expressions for the coefficients of the polynomials of F and to show that these coefficients never vanish for r in [0, 1] so that no solutions escape to infinity.
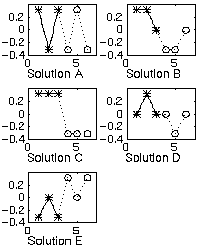
Fig. 3. Equivalence classes of initial solutions
Fig. 4 shows the successive values of rs for the equivalence class C
, a1 = -1.35 and r from 0 to 1. Note that 1s is a solution of the original system (1), which is otherwise not easy to find in
general. However, in case of class A
the numerical estimation procedure does not succeed to go further than r = 0.965 for a1=-1.1. The reason is that the arcs issued from two different initial solutions join
together at that value of r and disappear for larger values as explained in section 9. But as long as we can
follow a real solution s, we can find its stability by computing the eigenvalues
of DYs. Since Y=Q Q and the solutions under study are o. h., it is sufficient to compute the eigenvalues
of Q and to compare them to unity. Solution A
for instance rapidly becomes unstable.
8. Odd harmonic (o. h.) solutions
We have mentioned in section 6 that the initial solutions of the homotopy have an
o. h. symmetry. We now show that this is true for the trajectories A
to E
. These curves are sets of points where F(s, r)=0. Therefore they are integral curves of the ordinary differential equation:
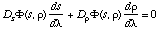 (11)
(11)
where Ds and Dr denote partial derivatives and l denotes arc length. If DsF(s, r) is non singular, then:
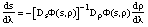 (12)
(12)
It is straightforward to verify that when s is o. h., 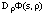 is o. h. also.
is o. h. also. 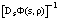 preserves this property, which implies that
preserves this property, which implies that 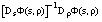 is o. h. as well. From (12) it is then clear that the curves A
to E
are composed of o. h. solutions. In consequence, any solution issued from the initial
ones is o. h.. We have observed in [Rodet 93f] that a slight breaking of the odd
symmetry of g can lead to the appearance of even partials, with large amplitudes if {hn} is not even symmetric.
is o. h. as well. From (12) it is then clear that the curves A
to E
are composed of o. h. solutions. In consequence, any solution issued from the initial
ones is o. h.. We have observed in [Rodet 93f] that a slight breaking of the odd
symmetry of g can lead to the appearance of even partials, with large amplitudes if {hn} is not even symmetric.
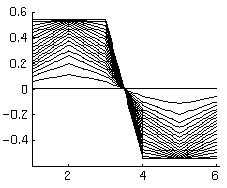 Fig. 4. Successive values of rs for the equivalence class C
of solutions, a1 = -1.35 and r from 0 to 1.
Fig. 4. Successive values of rs for the equivalence class C
of solutions, a1 = -1.35 and r from 0 to 1.
9. Direct computation on the example
The method consists of finding the equation of manifolds on which the solutions lie
and then finding the intersections of these manifolds as 1-dimensional manifolds
in a parametric form so that they can easily be explored for solutions. Here we use
the o. h. property of the solutions to find the solutions analytically in the previous example.
The system of polynomial equations (7) is:
x1 = h1g(x-3) + h0g(x-2) + h-1g(x-1) (13)
x2 = h1g(x-2) + h0g(x-1) + h-1g(x0) (14)
x3 = h1g(x-1) + h0g(x0) + h-1g(x1) (15)
Using the periodicity of the solution x, the symmetry h-1=h1, and the odd symmetry of g, we can rewrite the equations in x1, x2 and x3:
x1 = -h0g(x1) - h1g(x2) + h1g(x3) (16)
x2 = -h1g(x1) - h0g(x2) - h1g(x3) (17)
x3 = h1g(x1) -h1g(x2) - h0g(x3) (18)
This can be written in matrix notation x = N g(x), (19), i.e. N-1x = g(x), (20) where:
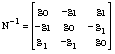 (21)
(21)
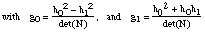
Using g(x) = x3+a1x, equation (20) leads to
x13 - (g0-a1)x1 + g1x2 - g1x3 = 0 (22)
x23 + g1x1 - (g0-a1)x2 + g1x3 = 0 (23)
x33 - g1x1 + g1x2 - (g0-a1)x3 = 0 (24)
Let a = g0-a1-g1. Using two equations to eliminate one variable, we get:
(x1+x2)(x12+x22- x1x2-a) = 0 (25)
(x1-x3)(x12+x32- x1x3-a) = 0 (26)
The two left hand terms of (25) and (26) define a plane and a cylinder with an ellipsoid
basis provided a > 0. Each ellipse can be described by a parametric equation with r =  :
:
x1 = r cos(w + p/6), x2 = r cos(w - p/6) (27)
x1 = r cos(m + p/6), x2 = r cos(m - p/6) (28)
The solutions are found on the intersection of the planes and cylinders. The intersection
of the cylinders 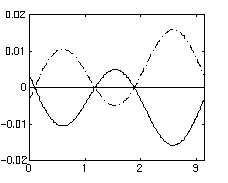
Fig. 5. Left hand term of (22) to (24) versus w.
is a curve obtained with m = - w or m = w - p/3. Then
we can follow this curve by using the parameter w and evaluating left hand terms of (22) to (24) for zero crossings. The values of
these terms versus w from 0 to p are shown on Fig. 5 for a1 = -1.1, h1 = 0.98 and h0 = 1-2h1 (two terms are identical). We observe common zero crossing for three values of w which correspond to the solutions designated previously by A
, D
and E
. The value of the left hand term of (22) versus w is shown on Fig. 6 for h1= 1-h1/2 and h0= 1., 0.98, 0.965, and 0.955. This explains how solutions designated by D
and E
join
together when h1 reaches 0.965 and then disappear as discussed in section 7. This occurs when a becomes negative because the ellipses collapse, leading to imaginary solutions. The
other solutions are easily found in the intersections of the planes with the ellipses
or between the planes. Finally we get the classes A
to E
previously found (Fig. 7).
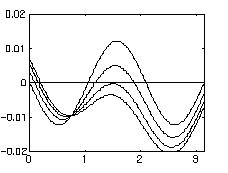
Fig. 6. Left hand term of (22) h0= 1., .98, .965, .955.
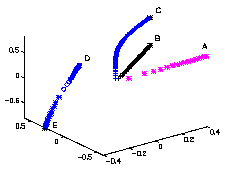 Fig. 7. The five classes of solutions of the example
Fig. 7. The five classes of solutions of the example
for h0= 1 to 0.
10. A rational function nonlinearity
As we mentioned in section 5, the choice of a polynomial g forces the existence of other points of functioning than the origin, which is serious
inconvenience for a musical usage [Rodet 93d]. We present here a rational function
nonlinearity
which
avoids that difficulty and can be studied with the same tools which we are using for
the polynomials. The most simple polynomial for our purpose is the one which we have
looked after in the previous sections, g(x) = x3 + a1x. Apart from the origin, it intersects the line y=x at two fixed points:
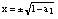 (29)
(29)
which in general are unstable. Furthermore, as xÆ , the slope of g Æ , which implies that the system can become unstable and escape to infinity, this is
rather annoying for a musical instrument.
We correct the behavior of g by dividing the polynomial by another polynomial of degree less or equal to 3. With
an even degree the odd symmetry is kept :
g(x) = (x3 + a1x)/(1 + b2x2) (30)
Then the system (1) has no spurious fixed points provided b2>1 and can be studied with the same tools as the polynomial case. This function is
shown on Fig. 8 for b2 = 2 and a1=-1.7. To keep things simple, let us consider the case where there is no
filtering in the 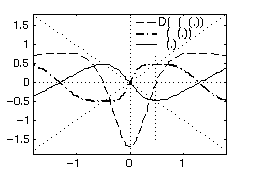 Fig. 8. Rational function g for a1 = 1.8 and b2 = 2
Fig. 8. Rational function g for a1 = 1.8 and b2 = 2
feedback loop (h0 = 1, h1 = 0). Then the first 2-periodic
solutions of (1) oscillate between points where g(x)=-x:
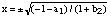 (31)
(31)
Such a solution is stable if the derivative of (g g(x)):
(g g(x))'
=g'
(g(x))g'
(x)=g'
(-x).g'
(x)=-(g'(x))2 (32)
is less than 1 in modulus at these points. This happens when -4 a1 -1. Fig. 8 shows g(x), (g g(x)) and (g g(x))'
for a1 =-1.7. But for approximately -6.15 a1 -4, we get two 2-periodic solutions. Finally chaotic solutions can be obtained for
a1 -7.2 approximately as shown on Fig. 9.
11. Conclusion
We have studied the class of single feedback loop systems with a single instantaneous
nonlinearity. It appears that both the number of solutions and the number of stable
solutions can be largely reduced by the presence of a low-pass filter in the feedback loop. For a system in the defined class we have defined an equivalent but simpler
system named the period-after-period system which has the same 2-periodic solutions.
In the case of a polynomial nonlinearity, it is possible to follow the solutions
from those of a trivial system, i.e. the one without a filter in the feedback loop, to the
solutions of the system with a specific filter. Having determined all the 2-periodic
solutions, it is easy to compute their stabilities. Finally we have proposed that
the nonlinearity be implemented as a rational function. This avoids any spurious functioning
point and guarantees that the oscillation of the system does not grow to infinity.
Furthermore, this rational function system exhibits a chaotic behavior with the simultaneous presence of harmonic sinusoidal components and of non sinusoidal components
which are heard as noise
added to the harmonic tone. This is a first step towards the control of physical
models.
Acknowledgements
We would like to thank Philippe Depalle, Adrian
Freed, Denis Matignon, Ami Radunskaya and Ina Steinecke for many useful comments
and discussions. We are grateful to CNMAT where this work was begun.
References
[Bergen 71]
A. Bergen & R. Franks, "Justification
of the Describing Function Method", SIAM J. Control, Vol. 9, No. 4, pp. 568-589,
Nov. 71.
[Chow 83]
S.N. Chow, J. Mallet-aret & J. Yorke, "A homotopy method for locating all zeros
of a system of polynomials", Lect. Notes in Math. 730, Springer-Verlag, 1979
Chua 90]
L. O. Chua and G.-N. Lin, "Canonical Realization of Chua's Circuit Family", IEEE trans. Circuits & Syst.
, Vol. CAS-37 (July. 1990) No. 7, pp 885-902.
[Freed 92]
A. Freed, "Tools for rapid prototyping of Musical Sound Synthesis Algorithms", Proc. International Computer Music Conference
, San Jose, pp. 178-181, Oct. 1992.
[Idogawa 92]
T. Idogawa, M. Shimizu & M. Iwaki, "Acoustical behaviors of an oboe and a soprano
saxophone artificially blown", Proc. of the symposium "Some Problems on the Theory of Dyn
. Systems in Applied Science"
, pp. 71-93, World Scientific, 1992.
[Ishizaka 72]
K. Ishizaka, J.L. Flanagan, Synthesis of Voiced Sounds from a Two-Mass Model of Vocal
Cords, Bell Syst. Tech. J., 51, 1233-1268.
[Mees 79]
A. Mees & L. Chua, "The Hopf Bifurcation Theorem and Its Applications to Nonlinear
Oscillations in Circuits and Systems", IEEE Transactions on Circuits and Systems
, Vol. Cas-26, No. 4, April 1979, pp. 235-254.
[Rodet 92a]
X. Rodet, "Nonlinear Oscillator Models of Musical Instrument Excitation", Proc. International Computer Music Conference
, San Jose, pp. 412-413, Oct. 1992.
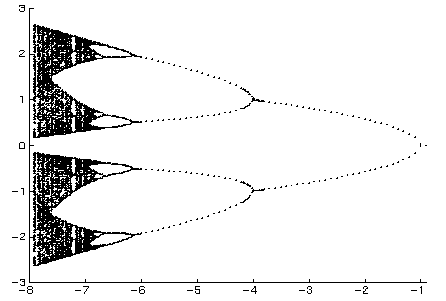
Fig. 9. Bifurcation diagram of the rational function nonlinearity versus parameter
a1.
[Rodet 92b]
X. Rodet & P. Depalle, "A physical model of lips and trumpet", Proc. International Computer Music Conference
, San Jose, pp. 132-135, Oct. 1992.
[Rodet 93a]
X. Rodet, "Sound and Music from Chua's Circuit",Journal of Circuits, Systems and Computers
, Special Issue on Chua's Circuit: a Paradigm for Chaos, Vol. 3, No. 1, pp. 49-61,
March 1993.
[Rodet 93b]
X. Rodet, "Models of Musical Instruments from Chua's Circuit with Time Delay", in
IEEE Trans. on Circ. and Syst., Special Issue on Chaos in nonlinear electronic circuits,
Sept. 1993.
[Rodet 93c]
X. Rodet, "Flexible yet controlable physical models", Proc. International Computer Music Conference
, Tokyo, Sept. 1993.
[Rodet 93d]
X. Rodet, "Applications of Chua's circuit to sound, music and musical instruments",
Proc. IEEE Workshop on Nonlinear Theory and Applications, Honolulu, Dec. 1993.
[Rodet 93e]
X. Rodet, "Chua's circuit and the first mode of the basic clarinet model", unpublished
internal report, IRCAM, Nov. 1993.
[Rodet & Steinecke 94a]
X. Rodet & I. Steinecke, "One and two mass models oscillations for voice and instruments",
unpublished internal report, IRCAM, March 1994.
[Rodet & Steinecke 94b]
X. Rodet & I. Steinecke, "Comparison and simulation of one and two mass physical
models for voice and instruments", in preparation.
[Sharkovsky & al 93]
A.N. Sharkovsky, Yu. Mastrenko, Ph. Deregel, and L.O.Chua, "Dry Turbulence from a
time-delayed Chua's Circuit", in Journal of Circuits, Systems and Computers
, Special Issue on Chua's Circuit: a Paradigm for Chaos, Vol. 3, No. 2, June 1993.
[Steinecke & Herzel 93]
I. Steinecke & H.H. Herzel, "Bifurcations in an asymmetric vocal fold model", Proc.
Symposium on Computer Simulation in Biology, Ecology and Medecine", Copenhagen, Aug.
23-25, 1993
[Steinecke 93]
I. Steinecke, Untersuchungen an einem vereinfachten Stimmlippenmodell, Diplomarbeit,
Humboldt-Universität, Berlin, 1993
[Valimaki et al. 93]
V. Valimaki, M. Karjalainen & T.I. Laakso, "Modeling of Woodwind Bores with Finger
Holes", Proc. International Computer Music Conference
, Tokyo, Sept. 1993.
[Wawrzynek 83]
PhD dissertation, Berkeley, 1983.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .




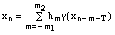 (3)
(3) C is the set of Fourier series of real periodic discrete signals of period length
2T:
C is the set of Fourier series of real periodic discrete signals of period length
2T: Rm2+T+1. The stability of a fixed point s of Y is given by the eigenvalues of DYs. The problem is therefore to find all the fixed points of Y or equivalently of P and M.
Rm2+T+1. The stability of a fixed point s of Y is given by the eigenvalues of DYs. The problem is therefore to find all the fixed points of Y or equivalently of P and M. R2T, is the circular convolution X X which is a polynomial in the variables {Xk, k=1,2,...2T}. Then Gk(X) is also a polynomial in the same variables and (5) for k=1,2,...2T defines a system
of 2T polynomial equations.
R2T, is the circular convolution X X which is a polynomial in the variables {Xk, k=1,2,...2T}. Then Gk(X) is also a polynomial in the same variables and (5) for k=1,2,...2T defines a system
of 2T polynomial equations.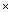 [0,1] Æ R2T, such that F(., 0) is M0(.) and F(., 1) is M1(.). More precisely, we are looking for the zeros of the system of polynomials M1(s)=s-P P(s). Suppose that M0(s) has known zeros, then under certain conditions, it is possible to follow the trajectories
of the zeros of F(s, r) starting from the zeros of M0(s) and going to those of M1(s) when r is varied from 0 to 1. However this is possible provided that no such zero escape
to infinity for some value of r in the interval [0,1] and that 0 is a regular value of F on R2T
[0,1] Æ R2T, such that F(., 0) is M0(.) and F(., 1) is M1(.). More precisely, we are looking for the zeros of the system of polynomials M1(s)=s-P P(s). Suppose that M0(s) has known zeros, then under certain conditions, it is possible to follow the trajectories
of the zeros of F(s, r) starting from the zeros of M0(s) and going to those of M1(s) when r is varied from 0 to 1. However this is possible provided that no such zero escape
to infinity for some value of r in the interval [0,1] and that 0 is a regular value of F on R2T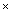 [0,1].The first requirement is easily fulfilled by making sure that the coefficients
of the highest terms of F in sn do not vanish. The second requirement guarantees that F-1(0) is a submanifold of dimension 1, i.e. consists only of arcs from a zero of M0(s) to a zero of M1(s), but it may not be fulfilled for some trajectories in our case. In our problem,
an interesting choice for M0 is the one for which, in the equation (3), h0 = 1 and hm=0 for m 0, M0(s)=s-g g(s), i.e. there is no filtering in the feedback loop. For simplicity we assume from
now on that g(.) is odd symmetric. Let W be the set of solutions of:
[0,1].The first requirement is easily fulfilled by making sure that the coefficients
of the highest terms of F in sn do not vanish. The second requirement guarantees that F-1(0) is a submanifold of dimension 1, i.e. consists only of arcs from a zero of M0(s) to a zero of M1(s), but it may not be fulfilled for some trajectories in our case. In our problem,
an interesting choice for M0 is the one for which, in the equation (3), h0 = 1 and hm=0 for m 0, M0(s)=s-g g(s), i.e. there is no filtering in the feedback loop. For simplicity we assume from
now on that g(.) is odd symmetric. Let W be the set of solutions of: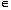 R. (8)
R. (8)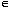 R2T, we retain only the vectors s such that sn
R2T, we retain only the vectors s such that sn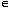 W for n=1,2, , 2T. The other solutions imply a value x
W for n=1,2, , 2T. The other solutions imply a value x 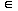 R, x 0, such that g(x)=x which we want to avoid since it corresponds to non-zero fixed points of the
original system, which give no sound. Note that for the solutions which we retain
sn= - sn-T for n=T+1,T+2, 2T. When a signal sn has this odd symmetry of the period with respect to its middle, we say that the signal
is odd harmonic
(o.h.) because its even harmonics are null. The initial solutions for the homotopy
are easy to build since they are the combinations of values from W. Another reason for this choice of M0 is as follows. The homotopy can simply be chosen as:
R, x 0, such that g(x)=x which we want to avoid since it corresponds to non-zero fixed points of the
original system, which give no sound. Note that for the solutions which we retain
sn= - sn-T for n=T+1,T+2, 2T. When a signal sn has this odd symmetry of the period with respect to its middle, we say that the signal
is odd harmonic
(o.h.) because its even harmonics are null. The initial solutions for the homotopy
are easy to build since they are the combinations of values from W. Another reason for this choice of M0 is as follows. The homotopy can simply be chosen as: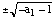 }=W. The initial solutions which we retain for the homotopy are obtained as the o.h.
signals with sample values in W, so that s - g g(s)=0. Two solutions are equivalent if they are identical by sign inversion or time
delay. Then, apart from the identically null solution which is irrelevant, there
are only 5 equivalence classes of solutions. These are shown in Fig. 3 and are designated
by the letters A
, B
, C
, D
, and E
.
}=W. The initial solutions which we retain for the homotopy are obtained as the o.h.
signals with sample values in W, so that s - g g(s)=0. Two solutions are equivalent if they are identical by sign inversion or time
delay. Then, apart from the identically null solution which is irrelevant, there
are only 5 equivalence classes of solutions. These are shown in Fig. 3 and are designated
by the letters A
, B
, C
, D
, and E
.
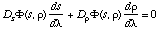 (11)
(11)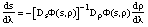 (12)
(12)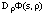 is o. h. also.
is o. h. also. 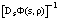 preserves this property, which implies that
preserves this property, which implies that 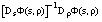 is o. h. as well. From (12) it is then clear that the curves A
to E
are composed of o. h. solutions. In consequence, any solution issued from the initial
ones is o. h.. We have observed in [Rodet 93f] that a slight breaking of the odd
symmetry of g can lead to the appearance of even partials, with large amplitudes if {hn} is not even symmetric.
is o. h. as well. From (12) it is then clear that the curves A
to E
are composed of o. h. solutions. In consequence, any solution issued from the initial
ones is o. h.. We have observed in [Rodet 93f] that a slight breaking of the odd
symmetry of g can lead to the appearance of even partials, with large amplitudes if {hn} is not even symmetric. Fig. 4. Successive values of rs for the equivalence class C
of solutions, a1 = -1.35 and r from 0 to 1.
Fig. 4. Successive values of rs for the equivalence class C
of solutions, a1 = -1.35 and r from 0 to 1.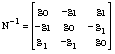 (21)
(21)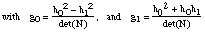
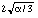 :
:

 Fig. 7. The five classes of solutions of the example
Fig. 7. The five classes of solutions of the example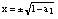 (29)
(29) Fig. 8. Rational function g for a1 = 1.8 and b2 = 2
Fig. 8. Rational function g for a1 = 1.8 and b2 = 2(31)
