
 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved. |
New Possibilities in Sound Analysis and Synthesis
Xavier Rodet, Philippe Depalle, Guillermo Garcia
ISMA 95, Dourdan (France), 1995
Copyright © ISMA 1995
Abstract
In this presentation we exemplify the emergence of new possibilities in sound analysis
and synthesis with three novel developments that have been done in the Analysis/Synthesis
team at IRCAM. These examples address three main activities in our domain, and have reached a large public making or simply listening to music.
The first example concerns synthesis
using physical models. We have determined the behavior of a class of models, in terms
of stability, oscillation, periodicity, and finally chaos, leading to a better control
of these models in truly innovative musical applications.
The second example concerns additive synthesis essentially based on the analysis
of natural sounds. We have developed a new additive method based on spectral envelopes
and inverse Fast Fourier Transform, which we name FFT-1 and which provides a solution to the different difficulties of the classical method.
Commercial applications are announced for this year, for professional users and soon
for a larger public.
The last example is an original work on the recreation of a castrato voice by the
means of sound analysis, processing
andsynthesis. It has been done for the soundtrack for a film and a CD about Farinelli,
the famous castrato of the eighteenth century. The CD and the film have reached millions
of people all around the world.
1. Introduction
Since the birth of computer music technology in the 1950's, new possibilities in
analysis and synthesis of sound have emerged from research institutions and have
come gradually in public use. In this presentation we will exemplify this emergence
by focusing on three novel developments that have been done by the Analysis/Synthesis team
at IRCAM. These examples are typical since they address three main activities in
our domain, synthesis, analysis and processing. They are typical also because they
are issued from laboratories and have reached not only professionals but also a large public
making or simply listening to music.
The first example concerns synthesis
using the class of models known as physical models [1], [2]. Compared to signal models,
such as additive synthesis, physical models have only recently received as much attention,
because, partly due to their nonlinear nature, they are very complex to construct and handle. But for musical applications, one should not merely build
models and deliver them to musicians. It is indispensable to go into the understanding
of the models, to conceive abstractions of them and to propose explanations useful
to the users. In particular, this comprehension is indispensable for elaborating
control of synthesis models, which are at the same time efficient and musically pertinent
[3]. Consequently, we have studied a family of differential and integral delay equations
which retain the essence of the behavior of certain classes of instruments with sustained sounds, such as wind, brass and string instruments [4]. We have determined
the behavior of our models, in terms of stability, oscillation, periodicity, and
finally chaos, leading to a better control of these models in truly innovative musical
applications.
The second example concerns one of the oldest methods of computer music called additive
synthesis, that is the summation of time-varying sinusoidal components, essentially
based on the analysis
of natural sounds [5], [6]. But despite rapid gains in computational accuracy and
performance, the state of the art in affordable single chip real-time solutions to
the problem of additive synthesis offers only 32 oscillators. Since hundreds of sinusoids
are required for a single low pitched note of the piano, for example, current single
chip solutions fall short by a factor of at least 20. And the development and use
of additive synthesis have also been discouraged by other drawbacks. Firstly, amplitude
and frequency variations of the sinusoidal components are commonly described in terms
of breakpoint functions. When the number of partials is large, control by the user
of each individual breakpoint function becomes impractical. Other arguments against
such breakpoint functions is that for voice and certain musical instruments, a spectral
envelope [7], [8] captures most of the important behavior of the partials. Finally,
the usual oscillator method for additive synthesis does not provide an efficient
way for adding colored noise to sinusoidal partials, which is needed to successfully synthesize
speech and the Japanese Shakuhachi flute, for example. This is why we have developed
a new additive synthesis method based on spectral envelopes and inverse Fast Fourier Transform, which we name FFT-1 and which provides a solution to the different difficulties that we have mentioned
[9], [10]. Commercial applications should appear this year for professional users
and soon for a larger public [11]
.
The last example is an original work on the recreation of a castrato voice by the
means of sound analysis, processing
and
synthesis [12]. It has been done to produce the soundtrack for a film and a CD about
Farinelli, the famous castrato of the eighteenth century. The film, realized by Gérard
Corbiau, and the CD produced by AUVIDIS, brings back to life a repertoire which could not be sung anymore. The musical consultant of the film Marc David has recovered
unedited scores from the French National Library. This example is particularly interesting
for several reasons. First it is extremely difficulty to synthesize high quality
(concert or CD) singing voice [13], secondly 40 minutes of a new castrato-like singing
voice have been produced in a limited schedule, thirdly it is the first application
of a technique which is analogous to morphing
and finally the CD and the film have reached millions of people all around the world.
2. Analysis, processing and synthesis
The work described here has been done at the Institut de Recherche et de Coordination
Acoustique/Musique (IRCAM), Paris, by the Analysis/Synthesis team. Since IRCAM is
devoted to musical research and production, our main goal, on a short term and a
long term basis, is artistic as well as scientific in nature. Computer generated music
occupies a central role in artistic production at IRCAM, in the form of aid and tools
for musicians and composers in the process of research and of the production of musical
compositions. Among activities of computer music that our team is devoted to, we can
mention sound analysis and processing, natural sound simulation and creation of new
types of sounds [14]. In order that these different musical objects be useful for
musical composition, it should be possible to modify them at will to introduce such effects
as expressivity or different playing techniques. Therefore, sounds should be defined
by models
which will be considered as instruments
. In the synthesis of musical sound as in many other fields of simulation, the concept
of model is essential for a better comprehension and use of the properties of sound
analysis and synthesis methods. In particular, it is necessary to understand the
structure of the space of instrumental
sounds.
Analysis of musical sounds is aimed at getting some precise information concerning
the signal itself, the way it has been produced or the way it is perceived [15],
[8]. Such an information can be very specific, this is the case of the fundamental
frequency, or it can be fairly general such as all the information which is needed to rebuild
a quasi identical sound with some synthesis technique [8].
Synthesis of musical sounds can be viewed as a two stage process. In the second stage,
the synthesizer itself computes a sound signal according to the value of parameters.
In the first stage, the determination of adequate values of these parameters is essential for getting the desired sound output. For example, parameters may be obtained
by some analysis technique [6] or generated by rules [16], [17], [18], [19], [20], [21].
Processing of musical sounds can be divided in two classes. On one hand, a processing
system may be independent of the signal: this is the case of modulation, filtering
or reverberation. On the other hand, a processing system may consist of an analysis
stage producing time dependent parameters, a modification of these parameters and a
synthesis stage from the modified parameters. A well known example of such processing
uses the so called phase vocoder
[22], [23].
An analysis or a synthesis method is always referring to some model of sound representation
and of sound production. This model can be the so called physical model
[24], [1] which is explicitly based on the physical laws which govern the evolution
of the physical system producing the sound. Or it can be a model of the sound signal
which consists in one or several parametered structures which are adapted to represent
and reproduce time domain and/or frequency domain characteristics of studied sounds
[25]. As these signal models
include few constraints, they are simple, general and low cost. This is the case
of an oscillator reproducing a periodic waveform extracted from a natural sound.
In between signal models and physical models, one can find models that share properties
with both classes : this is the case of a lattice filter as model of the vocal tract
or of some simplified physical models as proposed by J. Smith. But a more general
way to encompass both classes of models in the same formalism, is the so called State
Space representation studied in our team [26], [27]. One can always gradually transform a signal model into a physical one (or inversely),
by including (or removing) some constraints on the structure of the model [28]. According
to the previous requirements, our models rely on description of perceptually relevant features of the sound or of its Short Time Fourier Transform (STFT) or of the
system that has produced the sound. This description goes from the more general features
- e.g. spectral envelope - to the more subtle details, e.g. those of the STFT such as harmonicity, partials, and noise [7]. Parameters of a model are usually to be
updated at a rather low rate called frame rate or parameter rate (typically lower
than 200 Hz). Considering that the purpose is to allow musicians to process existing
sounds or to create new sounds, the control parameters have to be intuitive, direct, and
easy for musicians to use.
3. Understanding and Control of Physical Models
3.1 Introduction
This section describes an approach to the functioning of musical instruments from
the point of view of the theory of nonlinear dynamical systems. Our work provides
theoretical results on instruments, their models and on a class of equations with
delay, as well as on sound synthesis itself. Experimental and practical results open new
sonic possibilities in terms of sound material and in terms of the control of sound
synthesis which is particularly important for performers and composers of contemporary
music.
The complexity of physical models comes partly from their nonlinear nature. We try
to define resemblance and differences between several classes of instruments. This
attitude is necessary for artistic production which cannot be confined to traditional
instruments and for which we have to understand the structure of the space of instrumental
sounds. To fulfil these requirements, we have highlighted a characteristic common
to instruments with sustained sounds, i.e. the existence of delay terms in the equations
of models [29]. As a consequence, we have studied a family of differential and integral delay equations which are particularly difficult and are not well understood [30].
We have determined the behavior of our models, in terms of stability, oscillation,
periodicity, and finally chaos. Moreover we have found analytically some conditions
for these behaviors. We have realised digital simulations of our models on a workstation.
We have shown that observing in real time the solutions of an equation and their
properties, such as the Fourier spectrum, while changing parameter values, is a powerful tool for mathematical exploration.
An interesting finding is the control of chaotic behavior of our models [31]. It
seemed previously that chaotic sounds could not be of any musical interest. On the
contrary, we have found that these signals exhibit very interesting properties, such
as a clearly perceived pitch or an intermittent type behavior [32]. We have also shown
that a signal which is mathematically chaotic can be heard in a very different way.
What could be named the "proportion
of chaos" can be faint or predominant, from sounds perceived as harmonic without
noise, up to essentially noisy sounds. Finally, we want to control the "proportion
of chaos" in synthetic signals, opening a new field of fascinating research and application
[33].
3.2 Mathematical Model
The trumpet is an example of an instrument uncommonly difficult to model because
of the complicated features of nonlinear elements, lips and air flow between lips,
which are not easy to measure. We have studied such a model of the behavior of the
trumpet and we have tested its operation rather extensively [34]. Without further simplifications,
this system of five non-linear differential equations would be nearly impossible
to understand and control. To only compute a numerical solution would be very unsatisfactory for our musical and artistic purpose. This is why we have started the study
of the basic
behavior
of classes of instruments. In the case of the trumpet or of the clarinet, seen from
the mouthpiece, the bore appears roughly as a delay line with a sign inversion reflection
and some low pass filtering
[29]. The basis of the oscillatory behavior is to be
found in the coupling of the passive linear part with the nonlinear reed, and similarly
for string instruments, where the delay comes from transverse waves along the string.
In this way, many sustained musical instruments can be described by an autonomous
system of integral and differential delay equations. These equations are extremely
difficult and have not received as much attention as usual differential equations
[35]. However, a feedback loop formulation provides some light on their properties [36].
One of the simplest system is written, for x 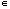 R, with a instantaneous nonlinearity g:
R, with a instantaneous nonlinearity g:
x(t) = h * g(x(t-t)) (1)
where g:R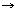 R, t
R, t 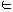 R is some time delay, h:R
R is some time delay, h:R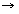 R is an impulse response and * is the convolution operator. Even in the case of this simplified equation (1), the
solutions and their stability are known only partially and in restricted cases
[37].
R is an impulse response and * is the convolution operator. Even in the case of this simplified equation (1), the
solutions and their stability are known only partially and in restricted cases
[37].
We have found a similarity between this model and the so called Time-Delayed Chua's Circuit
, a modification of the famous Chua's circuit governed by the same equation (1) which
we have simulated in real-time [38]. While the original Chua's circuit [39] happens
to be relatively difficult to control and does not offer as rich a palette of timbres
as wished for musical applications, the Time-Delayed Chua's Circuit is much richer
and flexible. A large variety of sounds can be produced by the system. This is due
to the combination of the rich dynamics of the nonlinear map together with the numerous
states represented by the delay line t as opposed to the minimum number of states of the original circuit. Information is
contained in these states and very complex signal patterns come out of the interaction
of the states through the nonlinear function. The feedback loop can also viewed as
a stabilisation
loop added on the original Chua's circuit to render its control much easier [40].
Therefore, the delay in natural instruments can be viewed the same way.
In the case of the clarinet the reed can be considered as massless, i.e. the nonlinearity
is instantaneous
, and the system is described by (1). In the case of the flute [41], [42], it seems
that there is essentially one nonlinearity but two feedback loops with different
delays. This still complies with equation (1) but the open loop transfer function
becomes a complicated combination of the influences of the two loops. In the case of the trumpet
or of the voice, the reed can no more be considered as massless, i.e. the nonlinearity
is not instantaneous [43]. Therefore, the model now consists of the nonlinear coupling of a feedback loop and a mass oscillating with one or several degrees or freedom
[44]. It seems that some important characteristic of the timbre of each of the previous
classes of instruments, particularly in the transients, is related to the corresponding basic structure as just described above.
3.3 Some results about the nonlinearity and the linear element
Let us consider a map g such that the origin O is a fixed point, with a slope s1 about O and a slope s2 at some distance from O. Two important characteristics of the sound, transient onset
velocity and richness, are controlled by the slopes s1 and s2 [38]. A.N. Sharkovsky [45] has shown analytically that the time-delayed Chua's circuit
exhibits a remarkable period-adding phenomenon. In some regions of the (s1, s2) plan, the system has a stable limit cycle with period respectively 2, 3, 4, etc.
In between every two consecutive periodic regions the system exhibits a chaotic
behavior. We have shown that in the k-periodic regions, the harmonics k, 2k, 3k etc.
are absent [32]. This is an interesting result from a musical
point of view as well. The map g can be simulated by a polynomial nonlinearity, or better, a rational function nonlinearity
[33].
Let us consider our system (1). The open-loop transfer function is:
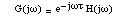
where H is the transfer function of h. The system does not oscillate if the limit
value 1/s1 lies to the left of all intersections of the Nyquist plot of G(jw) with the real axis. In the absence of the filter h or with a zero phase filter,
the delay leads to an oscillation frequency f0 = 1/2t. On the other hand the supplementary delay added by the filter h can move the oscillation
frequency away from 1/2t.
The intersections of G(jw) with the negative real axis define the frequencies of the modes of the instrument.
The system generally oscillates at the frequency of the strongest mode. If the argument
of G(jw) is different from zero, the modes can be moved away from harmonic positions. We
have shown that, when simultaneously g is not odd symmetric and there is a filter h, then even partials can appear. When
g is not very far from odd symmetry, if the argument of G(jw) is zero then the even harmonic partials are of small amplitude (clarinet). If the
argument of G(jw) is different from zero, then the even harmonic partials can be of large amplitude
(saxophone). The case where the argument of G(jw) is different from zero can lead to surprising results which look like quasi-periodicity
or inharmonicity.
Physical models often have more than one oscillating solution for a given setting
of their parameters. If the solution reached by the system is unpredictable, the
usage of a physical model will be rather difficult in a real-time musical performance.
Therefore, another of our goals is to study and limit the numerous stable solutions of
physical models. We have found that a path toward such a goal could eventually be
based upon the low pass character of the linear element [33].
3.4 Hopf bifurcation and periodic solutions
The Graphical Stability Test given above is valid as long as we can partition our
system into a instantaneous
nonlinearity and a linear feedback loop. Since we are interested in periodic oscillation,
we mention a more general method which allows us to prove of the existence of a periodic
solution when it occurs, and provides estimates for the frequency and amplitude of the oscillation. It also applies to an even more general class of systems encountered
with sophisticated physical models of instruments. The Graphical Hopf Theorem [36]
and its algebraic version apply to a nonlinear multiple feedback loop system where g is C4. Then under certain conditions on the nonlinearity g and the open-loop transfer function G, this theorem provides the existence, uniqueness
and test for the unique stable periodic solution required in our application.
3.5 Chaotic signals and musical applications
We have simulated our systems on a workstation [46] and we have written a graphical-user interface allowing for easy experimentation with
the parameter values and display of the output signal, of its Fourier Spectrum,
etc. Harmonic sounds and, in chaotic regions, noisy
sounds are obtained. Noisy sounds exhibit the simultaneous presence of harmonic components
and noise in the signal [32]. This is very interesting since this occurs for the
majority of natural instruments and since this is relatively difficult to model in
a way which is useful for musical purposes. The noisy and sinusoidal components coming
from our system are correlated and fuse
together. The control on the "proportion
of chaos" in the signal provides musicians with the possibility to control precisely
the amount
of chaotic
or noisy
components which they introduce in the signal [33]. Chaotic sounds, even when they
can be extremely noisy, keep some of the harmonic structure derived from the fundamental
frequency that corresponds to the delay t. The persistence of the harmonic structure in the chaotic signal is heard as a pitch
of the noisy sound! Moreover, the value of the pitch and the amount of tonal sound
perceived as compared to noise can easily be controlled. Finally, the gradual passage
from one periodic region to the next gives very innovative sounds, changing progressively from harmonicity to chaos but keeping at will more or less of the harmonic structure
induced by the delay line.
4. SPECTRAL ENVELOPES AND INVERSE FFT SYNTHESIS
4.1. Introduction
Many musical sound signals may be described as a combination of a pseudo-periodic
waveform and of colored noise [14]. The pseudo-periodic part of the signal can be
viewed as a sum of sinusoidal components, named partials
, with time-varying frequency and amplitude. Some of the first attempts at sound synthesis
were based on the method called additive synthesis,
that is the summation of time-varying sinusoidal components [5]. This signal modelling
approach inherits a rich history of signal processing techniques. As an example,
we have developed methods to automatically analyze sounds in terms of partials and
noise that can then be applied directly to additive synthesis [47]. In the sinusoidal
model, harmonic or inharmonic partials are easy to synthesize and partial parameters (frequency
and amplitude) can easily be mapped into the human perceptual space, are meaningful
and easily understood by musicians. Thus, additive synthesis is accepted as perhaps the most powerful and flexible method. However, its development and use have been
discouraged by severe drawbacks. This is why we have developed a new additive synthesis
method based on spectral envelopes and inverse Fast Fourier Transform, named FFT-1 [9], [10].
The first drawback of the classical oscillator method
of additive synthesis is the computation cost: a low pitch piano note that can sometimes
have more than a hundred partials. The FFT-1 method provides a gain of 10 to 30 versus the classical method. The second drawback of the oscillator method is the difficulty
of introducing precisely controlled noisy components which are very important for
realistic sounds and musical timbres. Our method makes noisy components easy to describe and cheap to compute. Last but not least, controlling hundreds of sinusoids
is a great challenge for the computer musician. A scheme based on spectral envelopes
renders this control more simple, direct and user friendly.
4.2. The oscillator method
Additive synthesis is usually done with a bank of sinusoidal oscillators. Let us
call J the number of partials of the signal to be computed at a certain time, that
is at a certain sample n. Let the frequency, the amplitude and the phase of the
jth partial, 1 j J, be named respectively fj, aj, and yj. More precisely, since they are functions of time, i.e. of n, we write them fj[n], aj[n], and fj[n]. Usually, fj[n] and aj[n] are obtained at each sample by linear interpolation of the breakpoint functions
which describe the evolution of fj and aj. The phase is redundant with the frequency and for simplicity we ignore it here.
For a sampling rate Sr, the jth partial is therefore defined by:
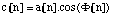 , with
, with 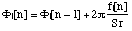
and the signal to be computed is: 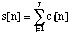 .
.
In the oscillator method, the instantaneous frequency and amplitude are calculated
first, by interpolation. Then the phase Fj[n] is computed. A table lookup is used to obtain the sinusoidal value of this phase
and the sinusoidal value is multiplied by aj[n]. Finally cj[n] is added to the values of the j-1 previous partials already computed. The computation
cost of the oscillator method is of the form a.J per sample, where a is the cost of at least 5 additions, 1 table lookup, 1 modulo 2p, and 1 multiplication. Even though it is possible to modify the sinusoidal oscillator
in order to produce large or narrow band-limited random signals by combined amplitude
and phase modulation, this has rarely be done.
4.3. Inverse Fast Fourier Transform additive synthesis
In our method [9], the computation of the partials is not done by a bank of oscillators
but by an Inverse Fast Fourier Transform (FFT-1) of short term spectra (STS) Sl[k] into the corresponding time-domain signals swl[n]. To better explain the method, let us consider first the analysis by FFT such
as used in the Phase Vocoder [22] which is familiar to many people: The signal s[n]
is first cut into successive frames sl[m] which overlap. Each frame is multiplied by a so called window
signal w[m] such as the Hanning window. With an appropriate choice of w and of the
overlapping factor d, s[n] can be exactly reconstructed from the windowed frames
swl[m] by the so called overlap-add
method [23]. Then the complex STS of each frame is computed by FFT, leading to a
succession of complex valued spectra Sl[k]. Now the FFT-1 method is easily understood as just the inverse process: Start from the spectra Sl[k], compute their Inverse FFT to get the swl[m] and overlap-add them in order to obtain the time-domain signal s[n].
For reasons of efficiency a partial is represented in a spectra by a few points
of non-negligible magnitude, typically K=7. To build the contribution of a given
partial in the STS Sl[k], we only have to compute these K spectral values and add them to Sl[k]. If N is the size of a frame (typically N=256), we find here a gain in computation
roughly proportional to N.d/K = 36. Other implementation optimisations are given
in [9], [10] and [48]. Simply note that the number K of significant values in the
spectrum W of the window can be adjusted at best by use of an auditory model. As a simple
example, partials with low amplitude require a smaller K.
In our FFT-1 synthesis method, we can introduce noise components precisely in any frequency band
narrow or wide and with any amplitude. We simply add in the STS under construction,
at proper places, bands of STS's of w windowed white noise signal. This is easy and
inexpensive if the STFT has been computed and stored in a table before the beginning
of the synthesis stage. There exist analysis methods, [49], [25], [47], [6],
to separate the noise components from the sinusoidal ones, allowing the preparation
of data for noise component STS's.
The FFT-1 algorithm has been implemented on the MIPS RISC processor of the SGI Indigo [46],
[48]. In terms of cost, one of the critical elements is the construction of a STS
Sl. By careful coding, many of the performance enhancing features of modern processors
[50], [51] may be used to efficiently implement the critical inner loop. The SGI
Indigo implementation takes advantage of the ability of the R4000 to overlap the
execution of integer address operations, floating point additions and multiplications, delayed
writes and multiple operand fetches into cache lines. It is interesting that the
table for the oversampled window transform is small enough to fit into on-chip data
caches of modern processors. This is not the case for the larger sinusoid table required
in standard oscillator based additive synthesis. A detailed comparison of different
implementations is given in [48].
4.4. Control by spectral envelopes
In usual implementations of additive synthesis, fj[n] and aj[n] are obtained at each sample by linear interpolation of breakpoint functions of time
which describe the evolution of fj and aj versus time. When the number of partials is large, control by the user of each individual
breakpoint function becomes impossible in practice. But in the case of the voice
and of certain instruments, a source filter model [7], [8] is a better representation of some of the behavior of the partials. Then the amplitude of a component is a
function of its frequency, i.e. the transfer function of the filter [7], [15]. That
is, the amplitude aj depends of some spectral function, named spectral envelope
, at the frequency fj. The amplitude variation induced by frequency variation such as vibrato can eventually
be very large [13]. To take into account these amplitude variation, a breakpoint
function of time may have many breakpoints.
Moreover, the amplitude of a partial is then not an intrinsic property of the timbre
independent of other characteristic such as fundamental frequency. Amplitudes stored
in breakpoint functions of time, also disallow modifications of fundamental frequency
or vibrato.
On the contrary, a spectral envelope can be described as an analytical function
of a few parameters, whatever number of partials it is used for. It can vary with
some of its parameters for effects such as spectral tilt or spectral centroid changes
known to be related to loudness and brilliance. Spectral envelopes can be obtained automatically
by different methods e.g. Linear Prediction analysis [8]. If the amplitudes and frequencies
of the partials are already known from sinusoidal analysis, the Generalized Discrete Cepstral analysis [52], [53], provides reliable envelopes, the smoothness
of which can be adjusted according to the order. We can use spectral envelopes defined
at specific instants, for example the beginning and the end of the attack, sustain
and decay of a note, etc. Then at any instant, the spectral envelope to be used is
obtained by interpolation between two successive recorded envelopes [21]. Frequencies,
phases and noise components also can be described by similar envelopes that we call
generalized spectral envelopes
. [19]
4.5. Applications
Our new method of additive synthesis by FFT-1 [54] brings a solution to the three main difficulties of classical additive synthesis.
The processing time (calculation cost) can be divided by a large factor. It is easy
and not costly to introduce noise precisely in any frequency band narrow or wide,
and with any amplitude. Control is made easier by use of spectral envelopes
instead of the time-functions classically used for additive synthesis. Under the
name F*A*R [11], the company OberheimDigital has developed a real time multi-timbral
instrument based on FFT-1. This instrument has all the possibilities of present day synthesizers, plus many
others such as the precise modifications of sampled sounds, speech and singing voice
synthesis.
5. The recreation of the voice of a castrato: Farinelli
5.1. Introduction
The recreation of a castrato voice by the means of sound analysis, processing and
synthesis has been done for a musical film about Farinelli, the famous castrato of
the eighteenth century [12]. The film, realized by Gérard Corbiau, and the CD of
the soundtrack produced by AUVIDIS bring back to life a repertoire which could not be sung
anymore. The musical consultant of the film, Marc David, has recovered unedited scores
from the French National Library. Forty minutes of processed singing voice have been
produced with a high level audio quality as needed for a CD.
Castrati were generally well known for the special timbre
of their voices. Their voices had not changed with puberty and, with maturity, castrati
lung capacity, chest's size, physical endurance and strength were generally greater
than those of normal males. Farinelli could sustain a note longer than one minute
and he could sing long phrases of more than two hundred notes without seeming to take
a breath. Their small and supple larynx along with their short vocal cords, allowed
them to vocalise in three octaves and a half and to sing with a great vocal flexibility, to sing rapidly large intervals, cascading scales and trills. All the more that
castrati were selected among the best child singers and trained very intensively.
Castrati's specific repertoire takes their high level singing technique into account,
therefore it is extremely difficult to sing. There is practically no recorded references.
The last castrato has recorded less than one hour of singing voice on wax cylinders. This historical recording has little technical utility due to its poor quality.
Nevertheless, we have taken into account the physical characteristics of the vocal
production system of the castrati, the global aesthetic of the historical recording
and descriptions found in the literature. The voice has also been designed according
to the wishes of the film and music producers.
5.2. Recording and editing of the voice
Two voices have been chosen, a counter-tenor, Derek Lee Ragin and a coloratura-soprano,
Eva Godlevska, with similar and good baroque singing techniques. The recording has
been made in the concert hall "L'Arsenal" in Metz, France by the Les Talens Lyriques
Orchestra conducted by Christophe Rousset. Due to artistical constraints, sound engineer
J.C. Gaberel was obliged to record voice and orchestra simultaneously, despite the
evident interest of a multitrack recording. One consequence is the presence of orchestra components at 20 to 30 dB under the mean average level of the singing voices.
This constraint obliged us to built very robust processing methods. The recording
was made on a Nagra IV-D machine with a precision of 20 bits. The remarkable editing,
sometimes note by note, has been made by J.C. Gaberel on a Sonic Solution machine.
5.3. Processing
First, as one of the artistic specifications was to make the finally processed voice
sound close to the counter-tenor one, we modify the soprano-coloratura parts to match
the counter-tenor timbre. This voice morphing
, constitutes the main and critical step of the scheme. Secondly, we give the voice
a more juvenile aspect by using global modifications. For instance, we attenuate
some high frequency bands to reduce the kind of breathiness found in Derek Lee Ragin's
voice. We
also make the voice sound brighter by modifying the spectrum envelope. Vowel timbres
not only depend upon phonemes, but also upon pitch and intensity. Thus, a reference
data base composed of all the combinations phoneme-pitch-intensity of the two voices
had to be set up.
Then the musical phrases to be processed must be segmented and labelled in terms
of singer, phoneme, pitch, power, begin and end times. Precise fundamental frequency
estimation is made by the algorithm described in [55]. A first segmentation pass
is performed automatically on the fundamental frequency evolution by a method recently developed
in our team [56], then begin and end times and labels of the vowels are adjusted
by hand in a second pass. Our voice morphing first consists in modifying the spectral envelope of the soprano voice to match that of the counter-tenor voice. This is achieved
by frequency domain filtering (the phase vocoder S.V.P., [22]). As scores are written
for castrati, most of the songs are high-pitched, and it's a common fact that in this case the frequency response of the vocal tract is poorly estimated. Then, voice
morphing would not reach the target timbre and the transformation could emphasize
some partials of the orchestra. One could imagine computing a Discrete Cepstrum envelope [57]. But the soprano-coloratura often changes continuously the shape of her vocal
tract when singing a cascade of notes on the same vowel. In addition, the tremolo
correlated to the vibrato effects makes spectral envelope estimation even more difficult.
Under such conditions, instantaneous spectrum envelopes becomes useless. In the middle
range frequencies (2.5 to 5 kHz), the spectrum envelope shape remains constant in
time for a given vowel note, it's global amplitude is modulated and this effect is
emphasized by the loudness. It follows that average spectrum envelopes are a good mean
to cope with these fluctuations. In the upper range frequencies (greater than 5 kHz),
the average level is perceptually more important than the precise shape of the spectrum. Therefore, we use the shape of the envelope weighted by a coefficient in order to
control the breathiness of the voice.
We build the filter frequency response in low frequencies by using additive synthesis
parameters [47]. These parameters, amplitudes and frequencies of the partials, are
used to impose on the processed sound the same relative amplitudes between harmonics
than those of the corresponding phoneme stored in the data base. Moreover, frequency
parameters are used to draw a frequency response which only acts on the vicinity
of each voice partial, in order to let the partials of the orchestra unchanged. The
width of each frequency response active band is computed according to the frequency deviation
due to the vibrato in the temporal window used by the phase vocoder. The phase vocoder
represents the sound without any loss of information and allows the application of any precise frequency response.
6. Conclusion
The developments detailed in this presentation exemplify new possibilities in sound
analysis and synthesis. On one hand, theoretical results have been obtained, e.g.
in the domain of physical models. These results allow the construction of better
computer instruments for musicians, by improving the versatility and the control of these
instruments, and by offering new sonic possibilities such as chaotic sounds.
On the other hand, applications which where impractical a few years ago, are now,
not only possible in research centers but also made available for a large public.
This is the case for the additive synthesis revivified by the FFT-l method. Experience with implementations on affordable desktop workstations has led
to a real-time multi-timbral instrument based on FFT-l. It has all the possibilities of present day synthesizers, such as the sound quality
of sampling, plus many others such as precise and unlimited modifications of recorded
sounds, speech and singing voice synthesis. The recreation of a new singing voice,
which would have been considered out of reach until recently, has been made possible
by improved processing techniques, precise sinusoidal partial analysis and frequency
domain filtering for instance. This result not only permits to bring back to life
the castrato repertoire which could not be sung anymore, but also reaches a public even
larger than amateur musicians. There is no doubt that other techniques will have
similar developments and success in the near future. Music will see a widespread
use of such computer generated sounds and computer assisted composition.
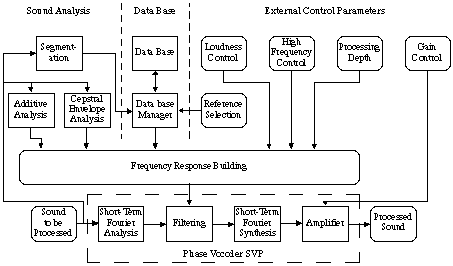
Figure 1 :
References
1.
"Modèles Physiques, Création Musicale et Ordinateurs
", Proceedings of the Colloquium on Physical Modeling, ACROE, Genoble,France, Oct.
1990, Editions de la Maison de Sciences de l'Homme, Paris, France, 1992.
2.
Keefe, D., "Physical Modeling of Wind Instruments", Computer Music Journal, MIT Press,
Vol 16 No. 4, pp. 57-73, Winter 1992.
3.
Cook, P., "A meta-wind-instrument physical model", Proc. International Computer Music
Conference, San Jose, pp. 273-276, Oct. 1992.
4.
. Fletcher, N.H., Rossing, T. D., The Physics of Musical Instruments
, Springer Verlag, 1991.
5.
Risset, J.C., Mathews, M.V., "Analysis of musical-instrument tones", Physics Today,
22(2):23-30, Feb. 1969.
6.
Depalle, Ph., Garcia, G., Rodet, X. "Tracking of partials for additive sound synthesis
using hidden Markov models", IEEE ICASSP-93 ,
Minneapolis, Minnesota, Apr. 1992.
7.
Rodet, X., Depalle Ph., Poirot, G., "Speech Analysis and Synthesis Methods Based on
Spectral Envelopes and Voiced/Unvoiced Functions", European Conf. on Speech Technol.,
Edinburgh, U.K., Sept. 87.
8.
Depalle Ph., "Analyse, Modélisation et Synthèse des sons fondées sur le Modèle Source-Filtre",
Thèse de Doctorat de l'Université du Maine, Le Mans, Déc. 1991, 175p.
9.
Rodet, X., "Spectral Envelopes and Inverse FFT Synthesis", Proc. AES, San Francisco,
1992.
10.
Depalle, Ph., Rodet, X. "A new additive synthesis method using inverse Fourier transform
and spectral envelopes", Proc. of ICMC, San Jose, California, Oct. 1992.
11.
"F*A*R Fourier Analysis Resynthesis, Tecnology Dossier", OberheimDigital, 1994
12.
Depalle Ph., G. Garcia, Rodet, X., "A virtual castrato (?!)", Proc. of ICMC, Copenhagen
Oct. 1994.
13.
Bennett, G., Rodet, X., "Synthesis of the Singing Voice", in Current Directins in Computer Music Research
, ed. M.V. Mathews & J.R. Pierce, MIT Press, 1989.
14.
Rodet, X., "Analysis and Synthesis Models for Musical Applications", IEEE Workshop
on application of digital signal processing to audio and acoustics, Oct. 1989, New
Paltz, New-York, USA.
15.
Rodet, X., Depalle Ph., "Use of LPC Spectral Estimation for Analysis, Processing
and Synthesis", 1986 Workshop on Appl. of Digital Sig. Process. to Audio and Acoust.,
New-Paltz, New York, Sep. 1986
15.
Cointe P., Rodet X., "FORMES: an Object & Time Oriented System for Music Composition
and Synthesis", Conf. Rec. 1984 ACM Symp. on Lisp and Functional Programing, Austin,
Texas, Aug. 1984.
17.
Rodet, X., Barrière, J.B., Potard, Y., "The Chant Project : from the synthesis of
the sung voice to synthesis in general",Computer Music Journal MIT Press, fall 84.
18.
Rodet, X., Depalle Ph., "Synthesis by Rule: LPC Diphones and Calculation of Formant
Trajectories", IEEE-ICASSP, Tampa, Fl., March 85.
19.
Rodet, X., Depalle Ph., Poirot, G., "Diphone Sound Synthesis", Int. Computer Music
Conference, Koeln, RFA, Sept. 88.
20.
Depalle Ph., Rodet X., Poirot,G., "Energy and Articulation Rules for Improving Diphone
Speech Synthesis", Proc. ESCA Int. Conf. on Speech Synthesis, Autrans,France, Sept.
90.
21.
Depalle Ph., Rodet, X., T. Galas, G. Eckel "Generalized Diphone Control", Proc. of
ICMC, Tokyo Sept. 1993, pp. 184-187.
22.
Depalle Ph. and Poirot, G., "A modular system for analysis, processing and synthesis
of sound signals", Proc. of the Int. Comp. Music Conf., Montreal, Canada, 1991.
23.
Moulines, E., Laroche, J., "Non-parametric methods for pitch-scale and time-scale
modification of speech", Speech Communication 16 (1995) 175-205.
24.
Smith, J.O., "Efficient simulation of the reed-bore and bow-string mechanism", Proc
1986 Int. Computer Music Conf., P. Berg, eds., Computer Music Assoc., San Francisco,
pp. 275-280, 1986.
25.
Serra, X. "A system for sound analysis/transformation/synthesis based on a deterministic
plus stochastic decomposition", Philosophy Dissertation, Stanford University, Oct.
1989.
26.
Depalle Ph., Rodet, X., D. Matignon, "State-Space Models for Sound Syntesis", IEEE
ASSP Workshop on Appl. of Digital Sig. Process. to Audio and Acoust., Mohonk, New
Platz, New York, Nov. 1991
27.
Matignon, D., Depalle, Ph., Rodet, X., "State space models for wind-instrument synthesis",
Proc. International Computer Music Conference, San Jose, pp. 273-276, Oct. 1992.
28.
Rodet, X., Depalle Ph., "Modèles de Signaux et Modèles Physiques d'Instruments",
Proc. of the Colloqu. on Physical Modeling, Genoble, France, October 1990 Editions
de la Maison de Sciences de l'Homme, Paris, France, 1992.
29.
McIntyre, M.E. et al., "On the Oscillations of Musical Instruments", JASA 74 (5),
Nov. 83
30.
Hale, J.K., "Dynamics and Delays", in Delay Differential Equations and Dynamical
Systems, Proc., 1990, S. Busenberg & M. Martelli (Eds.), Lecture Notes in Mathematics
1475, Springer Verlag, 1991.
31.
Madan, R.N., "Learning chaotic phenomena from Chua's circuit", Proc. 35th Midwest
Symp. on Circuits and Systems, Whasington, D.C., August 9-12, 1992.
32.
Rodet, X., "Flexible yet Controllable Physical Models: a Nonlinear Dynamics Approach",
Rodet, X., Proc. Int. Computer Music Conference, Tokyo, 10-15 Sept. 1993.
33.
Rodet, X., "Stability/Instability of Periodic Solutions and Chaos in Phyical Models
of Musical Instruments", Proc Int. Computer Music Conference, Copenhaguen, Sept.
1994.
34.
Rodet, X., Depalle Ph., "A physical model of lips and trumpet", Proc. International
Computer Music Conference, San Jose, pp. 132-135, Oct. 1992.
35.
Ivanov, A.F., Sharkovsky, A.N., "Oscillations in Singularly Perturbed Delay Equations",
in Dynamics Reported
, C. Jones, U. Kirchgraber & H.O. Walther edit., Springer Verlag, pp. 164-224, 1992.
36.
A. I. Mees, "Dynamics of feedback systems
", Wiley, 1981.
37.
Chow, S. N., Green, D. Jr., "Stability, Multiplicity and Global Continuation of Symmetric
Periodic Solutions of a Nonlinear Volterra Integral Equation", Japan Journal of Applied
Mathematics, Vol. 2, No. 2, pp. 433-469, Dec. 85.
38.
Rodet, X., "Models of Musical Instruments from Chua's Circuit with Time Delay", IEEE
Trans. on Circ. and Syst., Special Issue on Chaos in nonlinear electronic circuits,
Sept. 1993.
39.
Chua, L. O., Lin, G.-N., "Canonical Realization of Chua's Circuit Family", IEEE trans.
Circuits & Syst., Vol. CAS-37 (July. 1990) No. 7, pp 885-902.
40.
Rodet, X., "Applications of Chua's Circuit to Sound, Music and Musical Instruments",
Proc. 1993 Proc. 1994 Int. Symp. on Nonlinear Theory and its Applications, Hawai,
Dec. 1994.
41.
Verge, M.P., "Jet Oscillations and jet drive in recorder-like instruments", Acta
Acustica 2 (1994), pp 403-419.
42.
Rodet, X., "Basic structure and real-time implementation of J.M. Verge's flute model",
internal report, IRCAM, Mai 1995.
43.
Rodet, X., Steinecke, I., "One and two mass models oscillations for voice and instruments",
unpublished internal report, IRCAM, March 1994.
44.
Rodet, X., "One and two mass models oscillations for voice and instruments", to appear in
Proc Int. Computer Music Conference, Banth, Canada, Sept. 1995.
45.
Sharkovsky, A.N., Mastrenko, Yu., Deregel, Ph., Chua, L.O., "Dry Turbulence from
a time-delayed Chua's Circuit", in J. of Crts., Syst. and Comp., Special Issue on
Chua's Circuit: a Paradigm for Chaos, Vol. 3, No. 2, June 1993.
46.
Freed, A., "Tools for Rapid Prototyping of Music Sound Synthesis Algorithms and Control
Strategies", Proc. Int. Comp. Music. Conf., San José, CA, USA, Oct. 1992
47.
García, G., "Analyse des signaux sonores en termes de partiels et de bruit. Extraction
automatique des trajets fréquentiels par des modèles de Markov cachés", Mémoire de
DEA en automatique et traitement de signal, Orsay, July 1992.
48.
Freed, A., Rodet, X., Depalle Ph., "Synthesis and Control of Hundreds of Sinusoidal
Partials on a Desktop Computer without Custom Hardware", Proc. ICMC, Tokyo, 1993.
49.
McAulay, R.J., and Quartieri, Th. F., "Speech analysis/synthesis based on a sinusoidal
representation", IEEE Trans. on Acoust., Speech and Signal Proc., vol ASSP-34, pp.
744-754, Aug 1986.
50.
Hennessey, J. L., Patterson D. A., 1990, "Computer Architecture: A Quantitative Approach",
Morgan Kaufmann, Palo Alto, CA.
51.
Lee, E. A., "Programmable DSP Architectures", IEEE ASSP Magazine, October 1988
52.
Galas, T., Rodet, X., "A parametric Model of Speech Signals:Application to High Quality
Speech Synthesis by Spectral and Prosodic Modifications", Proc. ICSLP, Kobe, Japan,
1990, p.801-804.
53.
Galas, T., Rodet, X., "Generalized Functional Approximation for Source-Filter System
Modeling", Proc. Eurospeech, Genova, 1991, p.1085-1088.
54.
Freed, A., Goldstein, M., Goodwin, M., Lee, M., McMillen, K., Rodet, X., Wessel, D.,
Wright, M., "Real-Time Additive Synthesis Controlled by a Mixture of Neural-Networks
and Direct Manipulation of Physical and Perceptual Attributes", Proc Int. Computer
Music Conference, Copenhaguen, Sept. 1994.
55.
Rodet, X., Doval, B., "Estimation of Fundamental Frequency of Musical Sound Signals",
IEEE ICASSP, May 1991, Toronto.
56.
Cerveau, L., "Segmentation de phrases musicales à partir de la fréquence fondamentale",
Rapport de DEA ATIAM, IRCAM, Juin 1994.
57.
Galas T., Rodet X., "A new power spectrum estimation method: applications to acoustic
signals", IEEE Workshop on Appl. of Digit. Sig. Process. to Audio & Acoust., Oct.
1989, New Paltz, New-York, USA.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .



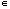 R, with a instantaneous nonlinearity g:
R, with a instantaneous nonlinearity g: 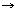 R, t
R, t 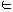 R is some time delay, h:R
R is some time delay, h:R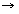 R is an impulse response and * is the convolution operator. Even in the case of this simplified equation (1), the
solutions and their stability are known only partially and in restricted cases
[37].
R is an impulse response and * is the convolution operator. Even in the case of this simplified equation (1), the
solutions and their stability are known only partially and in restricted cases
[37]., with
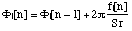
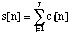 .
.