
 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved. |
One and Two Mass Model Oscillations for Voice and Instruments
Xavier Rodet
ICMC 95, Banff (Canada) 1995
Copyright © Ircam - Centre Georges-Pompidou 1995
Abstract:
Two movements seem possible for the lips of the trumpet player, upward
and outward striking
. A basic model, using one or the other movement, is proposed so that its behavior
can more easily be understood and controlled. The two movements are compared. The
model appears as a dynamic system of two loops coupled by a nonlinear function, one
loop describes the dynamics of the single mass and the other represents the acoustic wave
in the bore. Being much simpler, this model is simulated in real time on a workstation,
allowing for easy experimentation of different designs and parameter values.
I. Introduction
Physical models consisting of an instantaneous nonlinearity and a linear feedback
loop are relatively easy to understand and control [Rodet 93a]. But in the case of
the trumpet or of the voice, the assumption of a massless reed, hence of an instantaneous
nonlinearity, cannot be maintained. The movement of the lips of the trumpet player
is discussed for instance in [Yoshikawa 95]. It seems that two movements are possible,
as a function of several parameters such as the register and the shape of the bore.
The first movement is orthogonal to the flow - it is called upward striking
- and is comparable to the movement of the vocal cords. In the second movement, the
lip moves essentially back and forth - it is called outward striking
. In [Rodet 92], we proposed a physical model and simulation of the trumpet, of the
lips of the trumpet player and of the interaction between the two. The lip was modelled
as a rigid parallelepiped with two degrees of freedom acoustically coupled. This
leads to a system of five non-linear differential equations. The model exhibited behaviors
comparable to natural trumpet playing and produced sounds with typical brass
quality. Because of the complexity of the model, we underlined the necessity to devise
some playing
or control
model and concluded that much more work was needed to better analyze the physical
processes involved, to understand and represent them in a model simultaneously powerful
enough to render all the subtlety of natural sounds, yet simple enough to compute
and control. The research presented in this article brings some answer to these questions.
In particular we want to test whether one mass is sufficient to render the basic
properties of a trumpet oscillation. This allows a much simpler nonlinear dynamical
model, so that its behavior can be understood and controlled. This requirement is very
important for musical applications as explained in [Rodet 93a & 94a]. In section
III, we discuss and compare the force given by [Fletcher 91], the force which [Flanagan
68] uses for the one-mass model of vocal cords and the equations which we developed to
implement the model. All these models even if they do not represent a classical musical
instrument, are nonlinear dynamical systems which may have interesting musical properties. The simplest model appears as a dynamic system of two loops coupled by a nonlinear
function. One loop describes the dynamics of the single mass and the other loop represents
the acoustic wave in the bore. The upward and outward striking movements are compared. Being much simpler, this model is simulated in real time on a workstation,
allowing for easy experimentation of different designs and parameter values.
II. One Mass Model
Consider a mass m, the vertical only movement of which can close more or less an acoustic
tube (Fig. 1.).
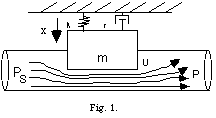
Let us call x the vertical position of the mass, A the area of the orifice, r the air density and Ps (s as in subglottal pressure by analogy with vocal cords) the blowing pressure that
generates some flow in the tube. We assume a Bernoulli flow in the orifice between
the mass and the opposite wall of the tube. Let us first follow the experimental
measurements of [van den Berg 57]. We designate by Bernoulli pressure the value
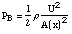
Then the acoustic pressure at the inlet (p1) and outlet (p2) of the glottal orifice are:
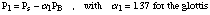 ,
,
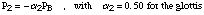
Let d be the mass thickness and l the orifice length. The pressure force when the
orifice is not closed is [Flanagan 68]
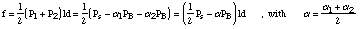
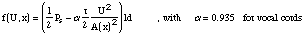
But the measurements of [van den Berg 57] are contested [Pelorson & al. 95]. Let us
now consider a different hypothesis and assume a jet flow out of the orifice. Then,
with sgn(Ps-P) designating the sign of (Ps-P):
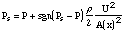
If the tube is open to the free atmosphere after the mass, P=0, there is no vertical
force on the mass! The jet flow is a simplification which leads to a non interesting
case for our simplest one-mass model uncoupled to any tube.
Using [Flanagan 68], we now consider the particular case where the tube opens into
the "free atmosphere" after the orifice between the mass m and the opposite wall
of the tube. This constitutes a one-mass model not coupled to any resonator. Let
us show that the volume velocity U passing through the orifice depends only on the pressure
Ps and on the area of the orifice which we suppose to be a function of x only. Therefore
the pressure on the mass is a function of x only for a fixed blowing pressure Ps. If the tube opens in the free atmosphere, the equivalent circuit, after [Flanagan
68], is shown on Fig 2.
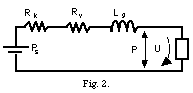
Because we are interested only in rather low frequency behavior, let us neglect Lg . Then
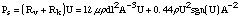
Therefore we can write U as a function of Ps and A only. We find the first term @101 and the second @104 for the maximum opening. But for small opening the first term should become comparable
or bigger than the second. Finally, the pressure force on the mass m is a function
of x for fixed Ps, say f(x) Similarly, when the orifice is closed, the force should depend only on
x. As a consequence the equation for the mechanical oscillator is:
(1)
where k>0 is the spring constant and r>0 is the viscous damping. The corresponding
state equation is:
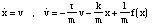
It is easy to show that, since the force depends only on x, for r > 0 this system
cannot oscillate in the sense that it does not have a periodic trajectory [Rodet
& Steinecke 94]. Different possibilities exist to make it oscillate:
- Have a force term which depends on the velocity
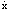 . The violin - i.e. bow-string interaction - is an example. It can easily be proved
that a one-mass model with a bow-string like force function
. The violin - i.e. bow-string interaction - is an example. It can easily be proved
that a one-mass model with a bow-string like force function 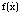 has at least one periodic trajectory.
has at least one periodic trajectory.
- Add one dimension to the system by adding a second mass leading to a two-mass model
where the two masses are linearly coupled (by a spring) and non linearly coupled
by the flow. This is made simple with the assumption of a jet flow through the minimum
opening [Steinecke 93]. Such two-mass model can oscillate
- Add a with memory
system (this adds some dimension) to the one mass. For instance a flow-pressure coupling
by a linear system, such as an acoustic tube, which can also be considered as a delay
term. We now focus on this case. It is simple since it consists of a one dimensional oscillator coupled to a delayed feedback loop [Rodet 93a]. It seems to model
some important behavior of trumpet like instruments.
III. One-mass coupled to an acoustic tube, the simplest trumpet-like model
We consider the same one-mass model as before but with an acoustic tube after the
mass, which induces a load on the mass oscillator. The effect of the tube can also
be seen as a delay term added to the system. Let P be the pressure in the mouthpiece.
The flow U depends on x and also on P as opposite to the uncoupled case studied in the preceding section.
Therefore, the pressure force on the mass is a function of x and P, say f(x, P) and
the mechanical equation is:
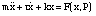
In [Fletcher 91]'s notation we have
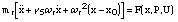
Let us now consider which pressure effectively acts on the mass. There are different
ways to derive the expressions for the force. We want to discuss and compare the
force given by Fletcher (a general equation to describe wind driven instruments),
the force which Flanagan uses for the one-mass model of vocal cords and the equations which
we developed to implement the model. All these models even if they do not represent
a classical musical instrument, are nonlinear dynamical systems which may have interesting musical properties.
III.1. Fletcher's model
Fletcher considers a mass-movement in the direction of the resulting flow, as shown
on Fig. 3. This is
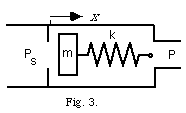
associated with a complicated "flow geometry". The resulting force is the sum of a
flow independent term which displaces the mass even if there is no flow and a flow
dependent term (a modified Bernoulli pressure). The "static", flow-independent, force
is very approximately proportional to the pressure difference Ps-P, because on the left side we have Ps and on the right side we have P. In detail, the situation is more complicated. This
force is diminished by a flow dependent term. For the idealized case this term is
proportional to the Bernoulli pressure PB. The force is then in Fletcher's notation:
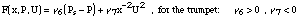
To calculate the volume flow velocity Fletcher uses the empirical equation

The parameters used for the trumpet correspond to a kinetic-only resistance in the
orifice. With this parameters the equation for the force results into:
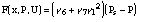
Remark:
Because of PB U2/X2 the Bernoulli pressure would not necessarily go to zero if x Æ 0. This behavior would be associated with a discontinuity in the force at x = 0.
But a > 1 includes the increased viscous resistance for small gaps. Then PB Æ 0 when l Æ 0
III.2 Flanagan's model
The movement of the mass is perpendicular to the direction of the flow. Pressures
are respectively Ps before the mass and P after the mass. To calculate the acting pressure Flanagan uses
the measurements of [van den Berg 57] and assumes a linear pressure change over the
thickness of the mass. As we have seen in section I, the resulting force is:
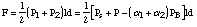
For calculating U, Flanagan considers the pressure drop over a viscous resistance
and a kinetic resistance. Here we neglect the inductance which describes the acceleration
of the flow.
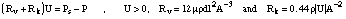
For large opening the term Rk is greater than the term Rv and 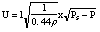
For the resulting force we get:
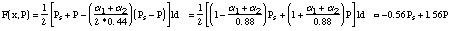
IV. Implementation
The geometry and the movement of the mass are considered as in the model of Flanagan,
but the pressure is considered as constant over the mass and equal to the pressure
before the mass Ps diminished by a modified Bernoulli pressure. The flow before the orifice is neglected
and a jet of the same cross section as the orifice is assumed after the mass. Then
we get a force:
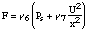
where g6 and g7 correspond to Fletcher's notation. From our point of view g6 = ld as in Flanagan's model. For an idealized Bernoulli flow and for Ps-P>0 we get:
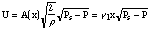
To include other losses we can use a parameter g1 as Fletcher does. Since Ps-P can be positive or negative,
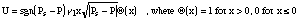 (2)
(2)
The resulting force is
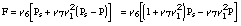
Remark:
Only the combination 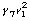 is used. Additional losses could be considered. To make the system as simple as possible,
an idealized flow is assumed, which leads to F = ldP:
is used. Additional losses could be considered. To make the system as simple as possible,
an idealized flow is assumed, which leads to F = ldP:
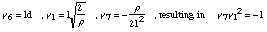
V. Comparison of the models
The model implemented is more or less equivalent to the model of Flanagan. We have
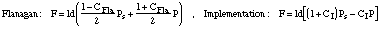
where 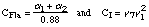 are constants of the corresponding models.
are constants of the corresponding models.
The resulting forces are equal when:
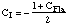
Setting 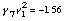 in the implemented model leads to Flanagan's model. Fletcher's model is really different,
because F = CFle(Ps-P) cannot be transformed into the other models by setting parameters. Therefore,
assuming that there is a motion in the direction of the flow, which is coupled to
the perpendicular motion [Rodet 92], we choose to add an empirical term which is
proportional to the pressure difference Ps-P. Then we have the complete pressure function for the open case:
in the implemented model leads to Flanagan's model. Fletcher's model is really different,
because F = CFle(Ps-P) cannot be transformed into the other models by setting parameters. Therefore,
assuming that there is a motion in the direction of the flow, which is coupled to
the perpendicular motion [Rodet 92], we choose to add an empirical term which is
proportional to the pressure difference Ps-P. Then we have the complete pressure function for the open case:
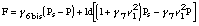 (3)
(3)
When the lips are closed there is no flow and the flow dependent term vanishes leaving
only the force which results from the coupling to the pressure difference. During
the impact we add an additional restoring force which is a linear function of x.
The corresponding spring constant is c = 3k. The equation of the mechanical oscillator is
therefore:
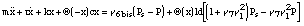 (4)
(4)
VI. Coupling of the mass and the tube
To make things as simple as possible, we reduce the bore to a cylindrical tube. We
then follow the formulation of [McIntyre et al. 83]:
 and
and 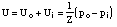
where y is the direction of the planar wave, the pressure p is the sum of the outgoing pressure
po and the incoming pressure pi, c is the sound velocity and the volume flow U at y=0, i.e. at the lips position,
is the sum of the flow of the outgoing and of the incoming waves. The volume flow
velocity and the pressure are coupled by the acoustical impedance in the tube Z =
rc/Acyl where r is the air density and Acyl is the cross sectional area of the tube. The pressure pi is calculated as a convolution of the outgoing pressure po with a reflection function r(t):
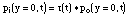
The reflection function r(t) can be formulated so as to make explicit the delay T
= 2L/c corresponding to one round trip when L is the effective length of the tube.
To get a simple model we often use only a reflection coefficient designated by reflect:
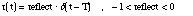
Finally, the pressure p is:
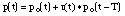
The acoustic tube is then coupled to the mechanical oscillator by the given equations
for the pressure P and the volume flow velocity U. The relationship for the Bernoulli
flow and the relationship for the wave in the tube are to be taken in consideration. Following [McIntyre et al. 83], values for P and U are obtained by solving the following
system of three equations:

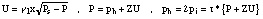
of variables P, U and ph. Then the system is solved by iteration. We take a given x and ph as the incoming pressure wave which is supposed to be not influenced by the outgoing
wave. Knowing ph we get U and P, these values are used to calculate the acting force on the mass and
solve the difference equation for x. Note that U and P depend on x which is taken
as a parameter to solve the equation and calculate the force. In the implementation
we have:
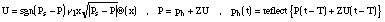
For 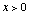 we get
we get
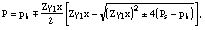 upper sign for Ps>ph, lower for Ps<ph,
upper sign for Ps>ph, lower for Ps<ph, 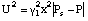
For  we get:
we get:
The graphical solution of U and P is shown in Fig. 4. For 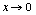 the curve 1 reaches the
the curve 1 reaches the 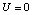 axis and the curve 2 results into P = ph. We can interpret the system as a circuit which consists of two loops. One loop describes
the dynamics of the mechanical oscillator. For a known pressure P we can solve the
differential equation for x which we use to calculate P which also depends on the
evaluation of the acoustic wave in the tube.
axis and the curve 2 results into P = ph. We can interpret the system as a circuit which consists of two loops. One loop describes
the dynamics of the mechanical oscillator. For a known pressure P we can solve the
differential equation for x which we use to calculate P which also depends on the
evaluation of the acoustic wave in the tube.
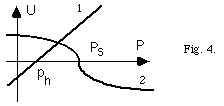
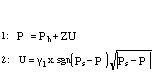
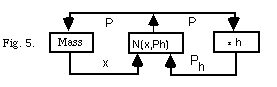
This is represented by the second loop which gives the pressure of the incoming wave
ph=2pi. Both loops are coupled by a nonlinear function to calculate P(x,Ph) and U(x, Ph) respectively. Finally, this can be simplified in P alone (Fig. 5).We think that this
system captures an important part of the behavior of trumpet-like instruments in
the interaction of the modes of the tube loop with the own resonance of the mass
subsystem [Rodet 92].
VII. Discussion of parameters
All values which are given here are in units of the SI system. Air density is r = 1.13 and sound velocity in air is c = 440.
Geometry of the lips
These values were chosen to be in the order of the real one and the bevavior of the
system does not seem to be very sensitive to precise values, but the influence of
variations in this range needs more investigation.
Length of the lip: l= 0.01, thickness of the lip: d = 0.005. Values used for the 2-mass
model of the vocal cords are smaller, the vibrating part of the vocal cords has a
thickness of d = 0.003.
Elastic properties of the lips
We take as standard for the mass m the value given by [Strong 90] and chose the spring
constant to the corresponding natural frequency given by Fletcher (w0 = 3100). The damping is set to get a quality factor 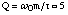 .
.
Mass of the lip: m0 = 1.5.10-4, stiffness of the lip: k0 = 1400, additional stiffness during closure c0 = 3k, damping constant r0 = 0.1. The natural frequency of the lips fLips is varied by using a tension factor tension
which scales the elastical properties in the following way.
m = m0/tension, k = k0.tension, c = 3k, r = r0. Thus, tension
gives the scaling of fLips.
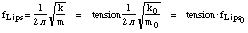
By keeping r constant, the Q-factor does not change. In the program we can use fLips as parameter and scale m, k, c and r in the given way. But then the damping factor
r/2m becomes small for lower frequencies. We can otherwise keep r/2m constant by
scaling r as r = r0/tension. This scaling results in more difficult playing of lower modes. The value
of r is not only important for oscillation onset, but also for the stability of modes.
Because r influences the frequency of the lips, it is possible to enter another mode
by an independent change of r.
Properties of the tube
The resonator is assumed to be a cylindrical tube of length L and cross sectional
area Acyl. From this geometry related parameters we get the acoustical properties: the acoustical
impedance Z and the resonance frequency fTube.
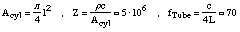
For the reflection at the open end we use:
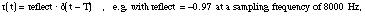
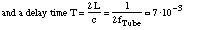
According to Fletcher the upper limit of the mouth pressure is around 10 kPa.
Empirical parameters
As mentioned above we assume an idealized flow and use the parameter  6scale to represent the ratio of the force which is parallel to the flow to that which is
orthogonal to the flow:
6scale to represent the ratio of the force which is parallel to the flow to that which is
orthogonal to the flow:
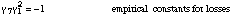


Then from equation 3 in section V the force term becomes:
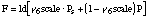 ,
,
Finally, to avoid a discontinuity in the force term, we use the function 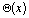 , (see equation 2 of section IV) in the right term also, as already written in section
V:
, (see equation 2 of section IV) in the right term also, as already written in section
V:
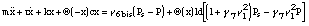
Discussion of  6scale
6scale
By changing  6scale,the dynamics of the system can be significantly influenced. For
6scale,the dynamics of the system can be significantly influenced. For  6scale = 0, F increases linearly with P. If
6scale = 0, F increases linearly with P. If  6scale = 1, F is proportional to ldPs. For
6scale = 1, F is proportional to ldPs. For  6scale > 1 the coefficient in P becomes negative, i.e. the higher pressure the smaller
force. Thus, for
6scale > 1 the coefficient in P becomes negative, i.e. the higher pressure the smaller
force. Thus, for  6scale < 1 a high pressure in the tube causes a strong force on the mass and for
6scale < 1 a high pressure in the tube causes a strong force on the mass and for  6scale > 1 the force becomes smaller and can become negative for large P. Additionally
to the discussed cases, the flow independant force of the Fletcher model is approached
for
6scale > 1 the force becomes smaller and can become negative for large P. Additionally
to the discussed cases, the flow independant force of the Fletcher model is approached
for  6scale > 1.
6scale > 1.
This different relationship between F and P leads to a different dynamic behavior.
If F increases with P, the mass follows the pressure, because the maximum of P corresponds
to the maximal force leading to a maximum of the displacement. For  6scale > 1 the minimum of P leads to the maximum of F. In this case the displacement
of the mass precedes the pressure which is more typical for the real trumpet. Nevertheless,
waveforms are in both cases nearly the same. We have found that the model is easy to play for higher values
6scale > 1 the minimum of P leads to the maximum of F. In this case the displacement
of the mass precedes the pressure which is more typical for the real trumpet. Nevertheless,
waveforms are in both cases nearly the same. We have found that the model is easy to play for higher values  6scale , i.e. 2.0, which corresponds to the outward striking. model.
6scale , i.e. 2.0, which corresponds to the outward striking. model.
VIII. Conclusion
We have implemented the systems described here above in HTM [Freed 92] allowing for
real-time synthesis and experimentation with various parameter and design choices.
The model behavior appears clearly connected to natural trumpet playing and the sounds
have some typical characteristics of brass
quality, in the transient at least since the model is extremely far from any natural
instrument. The simplest model appears as a dynamic system of two loops coupled by
a nonlinear function. One loop describes the dynamics of the single mass and the
other implemented with a delay, represents the acoustic wave in the bore. This is to be
compared with a basic clarinet model [Rodet 93b] which consists of one delayed loop
only and a basic flute model [Rodet 95] which consists of two delayed loops without
any mass. We are now testing and comparing the different configurations. Even though Flanagan's
and Fletcher models in our implementation can oscillate on several modes of the tube,
the second is easier to play and offers a larger range of playing values. We are also experimenting the behavior of the system in terms of stability, oscillation,
number of solutions and their stability, as well as the influence of parameter values
on the control of the system, such as speed of transients. We are also trying other
bore shapes and approximations, in particular to take into account the cup and the bell
of a trumpet. More details will be given at the conference as well as sound examples.
Acknowledgements
We thank Ina Steinecke who did a great part of this work and C. Vergez and N. Misdariis
[Misdariis 95] for many useful discussions and comments.
References
[Martin 42]
D. W. Martin, Lip vibrations in a cornet mouthpiece, J. Acoust. Soc. Am.
13
, 305-308, 1942
[van den Berg 57]
J. W. van den Berg, J. T. Zantema, and P. Doornenbal, Jr., On the air resistance and the Bernoulli effect of the human larynx, J. Acoust. Soc. Am.
29
, 626-631, 1957
[Flanagan 68]
J. L. Flanagan and L. L. Landgraf, Self-oscillating source for vocal-tract synthesizers, IEEE Trans. Audio and Electroacoustics, AU-16, 57-64, 1968
[Ishizaka 72]
K. Ishizaka and J. L. Flanagan, Synthesis of voiced sounds from a two-mass model of the vocal cords, Bell. Syst. Techn. J.
51
, 1233-1268, 1972
[Benade 76]
Benade (A.H.) -- Fundamentals of Musical Acoustics
(New York, Oxford Univerty Press,1976).
[McIntyre 83]
M. E. McIntyre, R. T. Schumacher and J. Woodhouse, On the oscillations of musical instruments, J. Acoust. Soc. Am.
74
(5), 1325-1345, 1983
[Smith 86]
Smith, J.O., "Efficient simulation of the reed-bore and bow-string mechanism", Proc
1986 Int. Computer Music Conf., P. Berg, eds., Computer Music Assoc., San Francisco,
pp. 275-280, 1986.
[Titze 89]
I.R. Titze, A four parameter model of the glottis and vocal fold contact area Speech,
Commmuniction 8, 191-201.
[Rodet 90]
Rodet, X., Depalle Ph., "Modèles de Signaux et Modèles Physiques d'Instruments",
Proc. of the Colloqu. on Physical Modeling, Genoble, France, October 1990 Editions
de la Maison de Sciences de l'Homme, Paris, France, 1992.
[Strong 90]
W. J. Strong, Computer simulation of a trumpet, J. Acoust. Soc. Am. Suppl. 1
87
, S138 (1990).
[Fletcher 91]
N. H. Fletcher and T. D. Rossing, The Physics of Musical Instruments, Springer-Verlag New-York 1991
[Cook 92]
Cook, P., "A meta-wind-instrument physical model", Proc. International Computer Music
Conference, San Jose, pp. 273-276, Oct. 1992.
[Freed 92]
A. Freed, "Tools for Rapid Prototyping of Music Sound Synthesis Algorithms and Control
Strategies", in: Proc. Int. Comp. Music. Conf., San Jose, CA, USA, Oct. 1992
[Keefe 92]
Keefe, D., "Physical Modeling of Wind Instruments", Computer Music Journal, MIT Press,
Vol 16 No. 4, pp. 57-73, Winter 1992.
[Matignon 92]
Matignon, D., Depalle, Ph., Rodet, X., "State space models for wind-instrument synthesis",
Proc. International Computer Music Conference, San Jose, pp. 273-276, Oct. 1992.
[Modèles 92]
"Modèles Physiques, Création Musicale et Ordinateurs
", Proceedings of the Colloq. on Phys. Modeling, ACROE, Genoble,France, Oct. 1990,
Editions de la Maison de Sciences de l'Homme, Paris, 1992.
[Rodet 92]
Rodet, X., Depalle Ph., "A physical model of lips and trumpet", Proc. International
Computer Music Conference, San Jose, pp. 132-135, Oct. 1992.
[Vössing 92]
H. Vössing, Experimentelle Untersuchungen zur Physik der Trompete, Diplomarbeit, Johann Wolfgang Goethe - Universität Frankfurt am Main, 1992
[Rodet 93a]
Rodet, X., "Flexible yet Controllable Physical Models: a Nonlinear Dynamics Approach",
Rodet, X., Proc. Int. Computer Music Conference, Tokyo, 10-15 Sept. 1993.
[Rodet 93b]
Rodet, X., "Models of Musical Instruments from Chua's Circuit with Time Delay", IEEE
Trans. on Circ. and Syst., Special Issue on Chaos in nonlinear electronic circuits,
Sept. 1993.
[Steinecke 93]
I. Steinecke, Untersuchungen an einem vereinfachten Stimmlippenmodell, Diplomarbeit, Humboldt-Universität, 1993
[Rodet 94a]
Rodet, X., "Stability/Instability of Periodic Solutions and Chaos in Phyical Models
of Musical Instruments", Proc Int. Computer Music Conference, Copenhaguen, Sept.
1994.
[Rodet 94b]
Rodet, X., Steinecke, I., "One and two mass models oscillations for voice and instruments",
unpublished internal report, IRCAM, March 1994.
[Verge 94]
Verge, M.P., "Jet Oscillations and jet drive in recorder-like instruments", Acta
Acustica 2 (1994), pp 403-419.
[Pelorson & al. 95]
Perlorson, X., Hirschberg, A., Wijnands, A.P.J., Description of the flow through
in-vitro models of the glottis during phonation,
[Rodet 95]
Rodet, X., "Basic structure and real-time implementation of J.M. Verge's flute model",
unpublished internal report, IRCAM, Mai 1995.
[Misdariis 95]
N. Misdariis and C. Vergez, Modèle de base du fonctionnement des instruments excités
par une lèvre vibrante, rapport de DEA, IRCAM, Juin 1995.
____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .
____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .




,
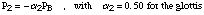
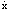 . The violin - i.e. bow-string interaction - is an example. It can easily be proved
that a one-mass model with a bow-string like force function
. The violin - i.e. bow-string interaction - is an example. It can easily be proved
that a one-mass model with a bow-string like force function 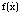 has at least one periodic trajectory.
has at least one periodic trajectory.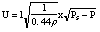
(2)
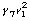 is used. Additional losses could be considered. To make the system as simple as possible,
an idealized flow is assumed, which leads to F = ldP:
is used. Additional losses could be considered. To make the system as simple as possible,
an idealized flow is assumed, which leads to F = ldP: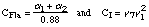 are constants of the corresponding models.
are constants of the corresponding models.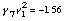 in the implemented model leads to Flanagan's model. Fletcher's model is really different,
because F = CFle(Ps-P) cannot be transformed into the other models by setting parameters. Therefore,
assuming that there is a motion in the direction of the flow, which is coupled to
the perpendicular motion [Rodet 92], we choose to add an empirical term which is
proportional to the pressure difference Ps-P. Then we have the complete pressure function for the open case:
in the implemented model leads to Flanagan's model. Fletcher's model is really different,
because F = CFle(Ps-P) cannot be transformed into the other models by setting parameters. Therefore,
assuming that there is a motion in the direction of the flow, which is coupled to
the perpendicular motion [Rodet 92], we choose to add an empirical term which is
proportional to the pressure difference Ps-P. Then we have the complete pressure function for the open case:(3)
(4)
and
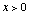 we get
we getupper sign for Ps>ph, lower for Ps<ph,
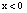 we get:
we get:
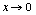 the curve 1 reaches the
the curve 1 reaches the 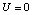 axis and the curve 2 results into P = ph. We can interpret the system as a circuit which consists of two loops. One loop describes
the dynamics of the mechanical oscillator. For a known pressure P we can solve the
differential equation for x which we use to calculate P which also depends on the
evaluation of the acoustic wave in the tube.
axis and the curve 2 results into P = ph. We can interpret the system as a circuit which consists of two loops. One loop describes
the dynamics of the mechanical oscillator. For a known pressure P we can solve the
differential equation for x which we use to calculate P which also depends on the
evaluation of the acoustic wave in the tube. 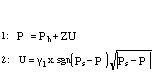
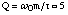 .
.  6scale to represent the ratio of the force which is parallel to the flow to that which is
orthogonal to the flow:
6scale to represent the ratio of the force which is parallel to the flow to that which is
orthogonal to the flow:,
 , (see equation 2 of section IV) in the right term also, as already written in section
V:
, (see equation 2 of section IV) in the right term also, as already written in section
V: 6scale
6scale 6scale,the dynamics of the system can be significantly influenced. For
6scale,the dynamics of the system can be significantly influenced. For  6scale = 0, F increases linearly with P. If
6scale = 0, F increases linearly with P. If  6scale = 1, F is proportional to ldPs. For
6scale = 1, F is proportional to ldPs. For  6scale > 1 the coefficient in P becomes negative, i.e. the higher pressure the smaller
force. Thus, for
6scale > 1 the coefficient in P becomes negative, i.e. the higher pressure the smaller
force. Thus, for  6scale < 1 a high pressure in the tube causes a strong force on the mass and for
6scale < 1 a high pressure in the tube causes a strong force on the mass and for  6scale > 1 the force becomes smaller and can become negative for large P. Additionally
to the discussed cases, the flow independant force of the Fletcher model is approached
for
6scale > 1 the force becomes smaller and can become negative for large P. Additionally
to the discussed cases, the flow independant force of the Fletcher model is approached
for  6scale > 1.
6scale > 1. 6scale > 1 the minimum of P leads to the maximum of F. In this case the displacement
of the mass precedes the pressure which is more typical for the real trumpet. Nevertheless,
waveforms are in both cases nearly the same. We have found that the model is easy to play for higher values
6scale > 1 the minimum of P leads to the maximum of F. In this case the displacement
of the mass precedes the pressure which is more typical for the real trumpet. Nevertheless,
waveforms are in both cases nearly the same. We have found that the model is easy to play for higher values  6scale , i.e. 2.0, which corresponds to the outward striking. model.
6scale , i.e. 2.0, which corresponds to the outward striking. model.