IRCAM - Centre PompidouServeur © IRCAM - CENTRE POMPIDOU 1996-2005.
Tous droits réservés pour tous pays. All rights reserved.

Musical Sound Signal Analysis/Synthesis: Sinusoidal+Residual and Elementary Waveform Models

Xavier Rodet

TFTS'97 (IEEE Time-Frequency and Time-Scale Workshop 97), Coventry, Grande Bretagne, août 1997
Copyright © IEEE 1997

Abstract

Several versions of Sinusoidal+Residual analysis/synthesis models have been developed for music applications. They have been very successful and are already found in commercial and experimental tools used by musicians as well as researchers. In this paper, we begin by presenting the principles of this now classical model. However, the standard version of the model suffers from limitations in various cases. We discuss some improvements of the standard method designed in order to overcome these difficulties. We then present and compare other analysis techniques which use Elementary Waveforms, i.e. waveforms localised both on the frequency and the time axis. In particular, the High Resolution Matching Pursuit algorithm is proposed as a potentially successful new direction of research.

1. Introduction

Some of the first attempts at sound synthesis were based on the method called additive synthesis, that is the summation of time-varying sinusoidal components [Risset & Mathews 69]. Additive synthesis is accepted as perhaps the most powerful and flexible method. An important advantage of additive synthesis over digital sampling is that it allows the pitch and length of sounds to be varied independently [Quatieri & McAulay 92]. The sample rate conversion technique [Smith & Gossett 84] used in digital samplers achieves pitch alterations by changing the rate at which sounds are read from memory. But this results in changes in the durations of those sounds. Furthermore, because independent control of every component is available in additive synthesis, it is possible to implement models of perceptually significant features of sound such as inharmonicity and roughness. In commercial digital samplers, sound amplitude and pitch are readily controlled, but no fine control over the sound spectrum is possible for timbre manipulations, such as continuous changes in harmonicity. Another important aspect of additive synthesis is the simplicity of the mapping of frequency and amplitude parameters into the human perceptual space. These parameters are meaningful and easily understood by musicians. This property is in contrast to, for instance, the parameter space of the frequency modulation synthesis method which maps awkwardly to the spectral domain through Bessel functions [Corrington 70]. Recently, a new additive synthesis method based on spectral envelopes and Fast Fourier Transform has been developed [Rodet & Depalle 92]. Use of the inverse FFT reduces the computation cost by a factor on the order of 15 compared to oscillators. This technique renders possible the design of low cost real-time synthesizers allowing processing of recorded and live sounds, synthesis of instruments and synthesis of speech and the singing voice.

In consequence, it is not surprising that additive analysis and synthesis of musical signals have recently received a great deal of attention. Even though the, now classical, additive sinusoidal analysis is based on rather simple principles, it has been very successful. The first goal of this paper is to examine this method, the reasons of its success and its weaknesses. The second goal is to try to extrapolate from our conclusions in order to propose new reasearch directions for musical signals analysis.

In section 2, we present additive sinusoidal analysis. The main drawbacks of the classical method are then explained in section 3 and some important improvements are briefly exposed. In section 4 we try to understand the advantages of additive analysis as well as its limitations. In section 5, under the term Elementary Waveforms, we present some new directions better suited for the analysis of musical sound signals.

2. The Additive Sinusoidal+Residual Model

Several similar sinusoidal models have been proposed for musical sound and speech signals [McAulay & Quatieri 86], [Serra 89]. They often incorporate a non-sinusoidal residual part which can be waveform coded or modeled as a random signal.

2.1 Presentation of the standard sinusoidal model

In the standard model, the sinusoidal part s(t) is represented as the sum of I sine waves ci(t), called sinusoidal partials, with time-varying parameters:

With ai (t)0 the amplitude and i(t) the phase of the sinusoidal partial:
ci (t)=ai (t)cos(i(t))

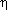A first important assumption underlying (often implicitly) sinusoidal models is that ci (t) locally ressembles a pure sinusoid. This means that a(t) should be a slowly varying signal, i.e. a low pass signal with a bandwith Ba and that i(t) is locally linear in t up to a small correction term. If locally around t0 is defined as t[t0-, t0+]: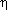

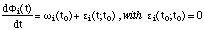
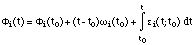
That i is small can be stated more precisely by saying that i(t) is a slowly varying signal, i.e. a low pass signal or that cos(i(t)) is approximately a band limited signal for t[t0-, t0+], with a bandwith Bf around i(t0). However, we will see in section 3 that the first assumption presented here above is only a rough approximation. In particular, the frequency behavior should not be formulated in terms of local variations of relative value but in terms of local variations of relative slope. Similarly, amplitude behavior should allow some fast variations such as is found in the attacks of percussive sounds.

Speech and musical sounds always have random components, often heard as a noise superposed for instance on the harmonic part. A second assumption often underlying a sinusoidal model is that the number I of sinusoidal partials is limited. Therefore, a purely sinusoidal model with slowly varying parameters can hardly represent all of a real signal x(t) and needs to be completed with a non-sinusoidal residual part r(t):

r(t) = x(t) - s(t)
Another argument in favor of a non-sinusoidal residual part r(t) is that the residual should be considered as a random signal in case of transformations such as time compression or expansion. In consequence, classical representations of random signals are better suited for the residual. It is common to represent only the short-time magnitude frequency content of the residual by a spectral envelope G(t,) [Serra 89]. If n(t) is a white gaussian noise and G(t,) is the Fourier Transform of a time-varying impulse response g([theta],t), then the model of the residual is:
This filtering can be implemented in the time domain or in the frequency domain. If R(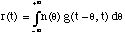,t) and N(,t) are the Short-Time Fourier Transforms of r(t) and n(t) respectively, then:

Fig. 1. Peaks found in successive analysis frames are grouped into tracks,i.e. sinusoidal partials.

2.2 Standard parameter estimation

Estimation of sinusoidal parameters is done in two steps. In the first step, a sliding window Short-Time Fourier Transform (STFT) is performed. Each peak of the magnitude spectrum is considered as the indication of a sinusoidal partial and its parameters are estimated. In the second step, peaks of successive analysis frames are grouped into tracks which are the sinusoidal partials under search (Figure 1).

Let x[n] be the analysed discrete signal, h[n] the analysis window and X(n,k) its STFT at time n and frequency k:

, (1)
Since we look at the STFT of a given frame around time n, let us drop index n and write X(k)=X(n,k) A peak of the magnitude of the STFT obtained by Discrete Fourier Transform of size N, |X(k)|, is found at index when
|X(-1)|<|X()|>|X(+1)|
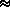
A peak at index supposedly indicates the presence of a sinusoidal partial at a near-by frequency (  ). The frequency i(t) and the amplitude ai(t) of this sinusoidal partial can be considered constant around time m, with values and A respectively. Henceforth, the shape of|X(k)| around index is the sampled shape of |H(-)|, i.e. of the Fourier Transform of h[n] translated at the frequency . To estimate and A, since h[n] is usually a symmetric window, one can use the second order approximation of H(-) around which is given by a quadratic function centered on . This is why a quadratic approximation of |X(k)|, in the neighborhood of index , is performed [McIntyre 92]. Then the center and the maximum amplitude of this function are taken as an estimation of and A repectively. Similarly, the local phase of the sinusoidal partial is obtained as a weighted average of the phase of X(k) in the neighborhood of index . The role of the weighting factor is to increase the importance of high amplitude values |X(k)| in order to diminish the effect of relatively low amplitude noise superposed on the sinusoidal partial.

The relatively simple detection and estimation procedure described here above has weaknesses which are detailed in section 3. However, it should be underlined that it has known a great success because it is fast and very robust. It can deal with the hundreds of sinusoidal partials encountered in musical signals and does not suffer from model-order determination and numerical or computational limitations which are common, for example, in parametric methods [Laroche & Rodet 89b], [Laroche 93a].

The second step of sinusoidal parameter estimation is the grouping of successive analysis frame peaks into tracks. This tracking is usually based on a heuristic approach [McAulay & Quatieri 86], [Serra 89] which matches peaks in successive frames while allowing deaths and births of tracks. It simply grows trajectories, iteratively frame after frame, in the direction of increasing time: for each frame successively, the tracks which still appear in the current frame are possibly continued provided there is a convenient peak in the next frame according to an optimal frequency match. When needed, some tracks are terminated and new tracks arise. We will not detail this algorithm here since we prefer a well grounded statistical approach presented in section 3.4.

Estimation of the spectral envelope of the residual signal around time t, G(,t), can be done with any usual AR estimation technique [Kay 88]. Such a technique provides the P coefficients ap(t) of an all-pole filter with magnitude transfer function G(,t). The coefficients ap(t) are well suited for time-domain filtering of a noise n(t) at the synthesis stage. In practice, the ap(t) are only estimated around successive times tl ,l=1, 2, 3,..., with a step tl+1-tl on the order of 5 to 20 milliseconds. Cepstral estimation can also be used on sliding window STFT R(,t) of r(t). Cepstral estimation provides P cepstral coefficients cp(t) which are well suited for frequency domain filtering of a noise n(t) at the synthesis stage. When estimating the spectral envelope G(,t), a nonlinear frequency scale, such as the Mel or the Bark scale, is appealing since is reflects some properties of human perception. Some authors [Serra 89], [Goodwin 96] have proposed to simply represent the magnitude short-time spectrum |R(,t)| by its mean value in channels distributed on such a nonlinear scale. This representation also is well suited for frequency domain filtering at the synthesis stage, since it requires only a mutiplication of the STFT of the noise n(t) by |R(,t)|.

3. Improvements of the standard model

Many improvements have been proposed beyond the standard model presented here above. In the following, we will only present some of the most important ones. Others can be found, for example, in [George & Smith 92],[Laroche & al. 93b], [Ravera & d'Alessandro, 94], [McAulay & Quartieri 95], [Pielemeier & Wakefield 96].

3.1 Peak detection and estimation

As mentionned in section 2.2, the presence in x(t) of a time-domain sinusoidal partial ci(t), around time t, is looked for by examining the SFT X(m,k). Let us again drop index n and write X(k)=X(n,k). If H() is the Fourier Transform of the analysis window h[n], this problem can be viewed as the detection of the presence of a scaled and sampled version of the signal H() in the signal X(k). Therefore, it is natural to look for the maxima of the cross-correlation function of H and X. If W is the bandwith of the low-pass signal h[n], then H() can be considered as negligible outside the interval [-W,W] and the computation of () is simplified:
Each maximum |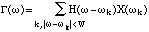()| indicates a sinusoidal partial candidate at frequency . An estimation of the amplitude A and of the phase of the partial can then be derived. Defining at a norm for H and X by:
and
we obtain:
Note that this computation also provides a measure v of the likeness between the observed peak and the peak which would result from a pure steady sinusoid (in which case v=1):

A sinusoidal likeness measure (SLM) v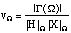 <1 indicates the presence of noise or of other sinusoidal components in the neighborhood of , or that the detected sinusoidal partial has fast varying parameters. The third case, fast variation, is examined in section 3.3 and 3.5. The second case, close-frequency partials, has been looked at by [Maher & Beauchamp 94]. If one can disregard the two last cases, then the SLM v is similar to the so called voicing index of speech signals. But the SLM v(n) is here a function of two variables, the analysis time n and the frequency . Errors on the speech voicing index at time n have serious consequences for speech coding or synthesis. On the other hand, errors on the SLM v(n) for some are of little consequence and are statistically compensated for by other v values. This SLM function v(n) has been very successfully used for speech coding or synthesis [Griffin & Lim 85], [Rodet & al. 87] as well as for musical sound analysis and synthesis [Rodet & al. 88], [Doval 94].

3.2 Parameter slope estimation

Several attempts have been made to extract information about the slope of sinusoidal parameters in a short time frame in order to overcome the limitation of mean values. Obtaining this information is not easy and usually suffers from uncertainty and errors. However, this information would be very useful when statistically combined with mean values, for example in the statistical approach presented in section 3.4.

In [Laroche 89a] a time-domain method is developped to estimate complex amplitudes (i. e. real amplitudes and phase deviations), when mean frequency values are known. Note that phase deviation is then equivallent to frequency variation. The model of the complex amplitude of the ith sinusoidal partial is a low order (e.g. 3) polynomial of time n:

The model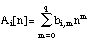 [n] of the signal is a sum of I sinusoidal partials. With zi=exp(ji):

, (2)
Let be the column vector =([1],[2],...,[N])t where N is the analysis frame length, bi=(bi,0,bi,1, ...bi,q)t, B=(b1|b2|...|bI)t and =[1|2|...|I|] where

Then we can write equation (2):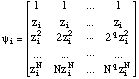
= B
Minimisation of
leads to: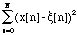
B=[h]-1h
The method has been applied successfully by [Laroche 89a] to find the amplitude and phase variations of sinusoidal partials of percussive sound signals, after the mean frequencies were found by Prony's method. This simultaneous determination of amplitude and frequency variations would be a useful complement of the classical sinusoidal analysis where mean frequency values are estimated on spectral peaks.

Naturally, sinusoidal partial parameter evolution also appears in the STFT, leading to a distorsion of peaks from the pure-sinusoid peak shape as mentionned in section 3.1. The distorsion caused by linear frequency modulation (LFM) and exponential amplitude modulation (EAM), in a given STFT X(k)=X(n,k), is examined in [Masri 96]. In the case of a pure sinusoid, the phase of the FFT bins, Arg{X(k)}, in the vicinity of the corresponding peak, is constant. In the case of modulation, this phase shows a variation (r) which is a function of the frequency r relative to the peak center. Experimental measures show that LFM, up to 16 bins of modulation per frame, causes a variation f(r) which is increasing with r for small |r|. Similarly, EAM, up to 6 dB of modulation per frame, causes a variation a(r) which is proportional to r for small |r|. Therefore, when only one type of modulation appears and is not too large, it can be estimated from the phase spectrum. Furthermore, for small |r|, the phase variations due to LFM and EAM are additive. But, since f(r) has even symmetry and a(r) has odd symmetry, their cumulative effect produces a global variation f(r)+a(r) with distinctive shapes according to the slope signs of f(r) and a(r). Therefore, simultaneous LFM and EAM can be estimated from the phase spectrum. The method has been successfully applied on simulated audio signals. However, for real musical signals, where additive interference from the more prominent peaks affects the phase profile accross less prominent neighbouring peaks, the described implementation is not resilient enough [Masri 96]. But it seems that the extracted slope information could be profitable at the partial tracking stage.

3.3 Reduced window length: parametric model of the STFT

In the standard sinusoidal analysis (section 2.2), sinusoidal partial candidates are found as peaks of the magnitude STFT |X(m,k)| of the signal x[n], as given by equation (1). In this equation, h[n] is a classical window, such as the Hamming window. The computation is done with a Discrete Fourier Transform [Rabiner & Schafer 78] and the k, k=1, 2, ... K, are regularly spaced frequencies. Since we consider the STFT for a given n, let us simply write X(k)=X(n,k). When two sinusoidal partials have nearby frequencies separated by 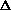f Hertz, in order that |X(k)| exhibit two peaks, it is necessary that the window length L is large enough:
L > q/f
where L is in seconds, q depends on the window main lobe width and is on the order of 3.5. Let us take for example a harmonic sound with a fundamental frequency of 110 Hz (which is heard as the note A2). Its sinusoidal partials are 110 Hz apart and L should be greater than 3.5/110, i.e. 32 ms. In polyphonic sound signals, partials can be even much closer and the length L should be accordingly larger. Note that the minimum frequency distance between sinusoidal partials is often unknown. A large window is a great inconvenience when sinusoidal parameters vary substantially over a time segment L. In particular, fast transitions such as consonnants or percussive attacks are smoothed. The problem is even worse for sinusoidal partials the frequency of which varies substantially. As an example, if the fundamental frequency varies by d Hertz on the window length L, then the ith partial varies of id When i is large, this important frequency modulation induces such a spreading of their spectrum that correponding peaks are smeared in |X(k)| and their detection fails. Another weakness of the standard sinusoidal analysis is that it does not take into account the influence of sinusoidal partials close in frequency which slightly alter the estimation of frequency and amplitude of a given sinusoidal partial.
The method presented in [Depalle & Tromp 96] and [Depalle & Hélie 97] remedies these difficulties by using a parametric model of the STFT of the signal and by allowing the window length to be as short as 2/f.Let us still write X(k)=X(n,k) for the STFT of the signal at time n. The model of the signal is based on the assumption of a sum of sinusoidal partials with amplitude and frequency constant over the window duration L, ai=ai[n] and i=i[n] and a local phase i:

Therefore, the model of the Fourier Transform is: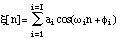
where H(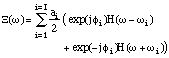) is the Fourier Transform of the analysis window h(n). The method consists in identifying the parameters for which the model best fits the observation X(k) according to a least squares criterion. The identification is realised by an iterative algorithm which alternatively improves the estimates of amplitudes using the previous estimates of frequencies and improves the estimates of frequencies using the previous estimates of amplitudes [Depalle & Hélie 97]. Initial estimates are obtained from the standard sinusoidal analysis using a relatively long window with a small bandwidth (e. g. a rectangular window). At each iteration, the amplitude optimisation is a simple linear problem. Since the frequency estimation problem is nonlinear, a simple linear optimisation is performed at each iteration: the equation is linearised around the vector {i-k, k=1, 2, ... K} in order to lead to a linear problem. One difficulty is that the algorithm can then converge, not to the main-lobe maximum, but to a secondary maximum corresponding to a sidelobe. In order to avoid that, Depalle and Hélie [Depalle & Hélie 97] have designed and used a new family of analysis windows without sidelobes. Other improvements of the algorithm are given in the above two references. This algorithm is shown to converge rapidly to the correct parameter values even when it is initialized with rather poor approximations. It also remains efficient at low signal-to-noise ratios (e.g. 10 power dB).

3.4 Statistical approach of partial tracking

During the second step of the analysis (see section 2.2), peaks found in successive analysis frames have to be grouped into partial tracks (Fig. 1). Some of the peaks do belong to partial tracks while others are spurious peaks (due to non-sinusoidal components for instance). The standard approach works well enough for some categories of sounds (harmonic, voiced, and slow time-varying sounds), but fails in presence of multiple harmonic structures, inharmonic partials, crossing partials, voiced/unvoiced transitions, and large frequency variations. Furthermore, this procedure takes into account frequency proximity only, neglecting other sinusoidal parameters, i.e. amplitude, phase and sinusoidal likeness measure SLM (section 3.1).

On the contrary, the procedure described in [Depalle & al. 93a], [Depalle & al. 93b], copes with these problems by globally optimizing the set of tracks. The peak tracking problem is formulated in terms of a Hidden Markov Model (HMM) [Rabiner 86]. The optimization is performed in a given time interval T according to a statistical criterion of slope continuity for all the sinusoidal parameters. Therefore, the optimal set of trajectories is found as the highest probability state sequence, by means of the Viterbi algorithm [Rabiner 86]. Note that the use of parameter slopes rather than parameter values, while being consistant with the first assumption of a sinusoidal model (see section 2.1), enables one to track time-varying partials as easily as constant ones, and solves the problem of detecting crossing trajectories.

We shall only indicate here a few features of the algorithm. Since the number of tracks can be in the hundreds, the biggest problem is to reduce computational complexity. Therefore, the Viterbi algorithm is applied on a window length of T frames, which slides frame by frame, and some constraints on index combinations, maximum number of tracks, etc., are added. Furthermore, the algorithm considers only the possible combinations of peaks between successive frames. Sinusoidal parameters are used to compute state transition probabilities [Depalle & al. 93] which favour slope continuity and disfavour spurious peaks. At time m, there are hm peaks Pm[i], 1 < i  hm. Each track is labelled by an index greater than zero. The problem is to associate an index Dm[i], 1 < i  hm, to each peak Pm[i]. When a peak Pm[i] is considered as a spurious one, it is associated with a null index Dm[i] = 0. A state Sm is defined by an ordered pair of vectors (Dm-1, Dm) and the observation is defined by an ordered pair of integers (hm-1, hm). The optimal sequence of states Sm=(Dm-1, Dm) is found by means of the Viterbi algorithm, which maximises the joint probability of state and observation sequences leading to a globally optimal solution. Then the tracks are defined by the sequence of vectors Dm from the state sequence.

This algorithm has been implemented at IRCAM by G. Garcia. Other computational cost reductions have been applied. In particular, the Viterbi algorithm has been replaced by a more efficient one taking advantage of the factorised structure of transition probabilities and eliminating computational redundancy. IRCAM's HMM tracking algorithm has been successfully used for sound analysis, processing and synthesis for research and for musical creation. As an example, it is possible to analyse polyphonic music comprising simultaneously several instruments, chords and percussion sounds. Examples will be played at the conference.

3.5 Fast transients

As mentioned in section 2.1, a sinusoidal model is based on an assumption of bounded local variations of relative slope of sinusoidal parameters. However, it should allow some fast amplitude variations such as found in the attacks of percussive sounds. Standard sinusoidal analysis based on STFT requires a rather long signal window (typically 30 ms) which smears such fast transients. To overcome this difficulty, Masri [Masri 96] detects fast transient instants and takes them into account when positioning analysis windows. The aim is to guarantee that spectra on either side (which are essentially different) are never captured in the same window. Furthermore, the method disallows any peak linking or spectral interpolation (for the residual part) across the event boundary. During the synthesis stage, a fast crossfade is performed at the event boundary to retain the abruptness of the original sound. In particular, at the synthesis stage, the crossfade length is kept constant even though the sound is time-stretched. The method has been successfully applied to mixtures of continuous and percussive sounds and preserves perceptual properties of both types of sounds.

4. Discussion of the sinusoidal model

The sinusoidal+residual model has been very successful for musical signal analysis, processing and synthesis. Several commercial and experimental systems are currently used by musicians [Rodet & al. 88], [Serra 89], [Fitz & al. 95], [Rodet & Lefèvre. 96]. Let us present some of the reasons for this success. A first one is the nature of musical sound signals. They often are composed of damped sinusoids of quasi-steady frequency (percussive sounds) or have relatively long and steady harmonic sustained parts. It is clear that a sinusoidal model is well adapted to represent a steady harmonic sound. It is probable that the nature of human perception of musical sound signals constitutes another reason. Human perception is extremely precise in steady sustained parts where sinusoidal analysis is the most efficient, and apparently less precise in fast transients where sinusoidal analysis is less performant. It seems also that locality, or better, redundancy in time and locality in frequency, of sinusoidal analysis largely contributes to its quality. In particular, each peak of the STFT is modeled independently and hence precisely when the peak is due to a quasi-sinusoid since corresponding spectral peaks are easy to measure accurately. Not only estimation errors are small but they tend to be statistically distributed in frequency and time, amounting only to a nearly inaudible level of distorsion.

However, there are sound signals for which sinusoidal analysis does not seem so well adapted, typically signals where excitation departs from periodicity. Curiously enough, sinusoidal analysis is also used for speech signals even though they often fall in the last category. The classical model of glottal speech production [Fant 70] consists of short pulses filtered through the vocal tract. Firstly, variations of vocal tract transfer function can be appreciable at the time scale of three glottal periods. Secondly, time locations of pulses can be far from periodical. We already noted in section 3.3 that high rank partials cause difficulties even for small fundamental variations. Figure 2 shows another case, i.e. a speech waveform resulting from irregular pulses, as often occurs at the end of a sentence (it is sometimes called vocal fry). Sinusoids make sens when, in a given frequency band, a waveform repeats periodically at least three times. On the contrary, signals like the one in figure 2 suggest the use of other methods based on waveforms better localised in time when needed, sometimes called Elementary Waveforms (see section 5).

Finally, the standard noise source and filter model represents non-sinusoidal and random components in a very unsatisfactory way [Goodwin 96]. Moreover, the fact that two totally different analysis techniques are needed is a weakness which leads to difficulties since the separation of sinusoidal and random components is not based on any solid grounding.

Figure 2. A speech waveform resulting from irregular pulses, as often occurs at the end of a sentence.

5. Elementary Waveform analysis

5.1 Presentation

Under the name Elementary Waveforms (EW) we group a certain number of methods using waveforms well localised in frequency and amplitude which are overlapped and added to construct a signal. As a first example, Formant Waveforms (called FOF from the French Formes d'Onde Formantiques) [Rodet 80] have been used for speech and musical signal synthesis. A FOF analysis method has been proposed in [d'Alessandro & Rodet 89]. Locality infrequency is adapted according to formant regions of the signal under analysis. Pitch Synchronous Overlap Add (PSOLA) is one of the most successul method for speech synthesis. In PSOLA analysis, segments extend over two pitch periods exactly. However, these segmented waveforms are not localised in frequency and usually no further analysis is done.

In [Liénard 87], a narrow band-pass filter bank is used to ensure locality in frequency. The signal at the output of each filter is segmented at successive minima of its amplitude envelope. Each segment is considered as an EW. The method has been used for speech analysis and synthesis.

Note that sinusoidal analysis starts with a STFT at arbitrary regularly spaced times, then look for specific peak patterns in the STFT. On the other hand, some EW analyses start with arbitrary regularly spaced band-pass filtering, then look for specific patterns in filter outputs. Matching Pursuit, presented here below, does not favour time or frequency but, at each step, looks for a time and a frequency elementary waveform position, as well as a scale, which are optimal according to the properties of the signal under analysis.

5.2 Matching Pursuit (MP)

Usual time-frequency and time-scale analysis methods, such as STFT [Rabiner & Schafer 78] or Wavelets [Kronland-Martinet 88] perform a decomposition of signals on a given fixed basis. Therefore, the analysis spreads some important structures of musical signals on many basis vectors. Regrouping the results of the decomposition of these structures, for recognition or processing, becomes difficult. For instance, musical signals include fast transients which are well represented by short waveforms and sustained parts which are more efficiently represented by long waveforms with short frequency support. We have seen in sections 2 and 3 that the usual analysis methods lead to difficulties with transients. New adaptive approaches have been developped in order to choose the decomposition vectors depending upon signal properties (e.g. [Coifman & Wickerhauser 92]), but they still use an orthogonal basis. Therefore, some important strcutures still tend to be spread on many vectors.

Pursuit algorithms, such as Matching Pursuit (MP) [Mallat & Zhang 93] or Basis Pursuit [Chen & Donoho 95] have been designed to overcome these difficulties. The decomposition vectors are selected among a redundant family, called a dictionary, of EWs well localised in frequency and time. In MP, the EWs which constitute the dictionary have three parameters, a scale factor s, a time position u and a modulation frequency (note that, unlike in Wavelets, scale and frequency are independant). With =(s,u,):

is a Gaussian fonction with unit norm. A MP is an iterative algorithm which decomposes a signal x over dictionary vectors as follows. Let us write Rnx a residue at step n, starting from R0x=x. At each step, the vector selected in the dictionary is the one which matches Rnx at best, i.e. such that: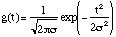
,
where is the set of all possible values for and C(x,g) is a correlation function which measures the similarity between x and g. The residue for the next step is then:

Finally, the signal is represented as: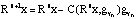
In [Mallat & Zhang 93], the correlation function C is the inner product C(x,g)=<x,g>. This decomposition is relatively fast to compute, gives a good resynthesis with a limited number of vectors and exhibits the different structures of the signal at different scales [Gribonval & al. 96a], [Gribonval & al. 96b]. However, these references show that the chosen correlation function C leads to inadequate representations of some structures, such as a sinusoid the envelope of which varies rapidly. Therefore, a High Resolution MP (HRMP) algorithm is introduced. It uses a different correlation function which allows the pursuit to emphasize local fit over global fit at each step. HRMP performs a better time-resolution than MP so that, in audio applications, attack-patterns recognition or processing is improved.

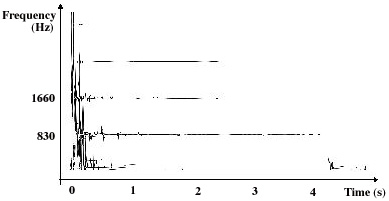
Fig. 3. Time-frequency distribution of a G5 sharp piano note, obtained with HRMP

The time-frequency distribution of a G5 sharp piano note, obtained with HRMP, is displayed in figure 3. One can easily distinguish long horizontal lines due to large-scale vectors well defined in frequency around 830 Hz, 1660 Hz, etc.. They correspond to the damped sinusoidal quasi-harmonic modes of the string. On the contrary, vertical lines corresponding to small-scale transient structures are visible at the attack and at the release of the damper of the piano. This example shows how HMRP provides a time-frequency representation adapted to the specificities of sound signals. The elements of this representation are easily related to perceptually important structures such as fast transients, or sustained sinusoidal partials.

6. Conclusion

The principles of sinusoidal+residual analysis have been exposed in order to better explain the reasons for its success and of its weaknesses. Some important improvements to the standard analysis technique have also been presented. Then, we have critically examined the overall method. Whereas sinusoidal representation is rather adequate for some musical signals, it seems inadequate for others. Locality in time and frequency and adaptation to signal properties is found to be an advantage of the method while the grouping of local features in larger scale sinusoidal partials, on a statistical basis, is shown to be very efficient. However, when the sinusoidal model is inadequate, other methods can give better results. In particular, more emphasis on local fit to the signal is advantageous for adaptive algorithms such as HRMP as well as for the sinusoidal model. But many aspects still need continued development. For instance, repeated pulses with a changing period cannot be easily modeled in a sinusoidal method. A good solution in HRMP analysis for this problem has also not yet been found. Similarly, random components require a totally different analysis technique in the sinusoidal+residual case. In HRMP, these components lead to a large number of Elementary Waveforms which still need to be grouped in order that processing or recognition can be performed.

References

[d'Alessandro & Rodet 89] C. d'Alessandro, X. Rodet, Synthèse et Analyse-Synthèse par Fonctions d'Onde Formantiques, J. Acoustique 2 (1989) pp. 163-168.

[Chen & Donoho 95]S. Chen, D. L. Donoho, Atomic decomposition bt basis pursuit, Technical report, Statistics Department, Stanford University, 1995.

[Coifman & Wickerhauser 92]R Coifman, M.V. Wickerhauser, Entropy based algorithms for best basis selection, IEEE Trans. Inform. Theory, 38 (2):713-718, P&rch 1992.

[Corrington 70] M. S. Corrington, Variation of Bandwidth with Modulation Index in Frequency Modulation, Selected Papers on Frequency Modulation, edited by Klapper, Dover, 1970 [Depalle 93a] Ph. Depalle, G. García, X. Rodet. Tracking of partials for additive sound synthesis using hidden Markov models. IEEE ICASSP-93 , Minneapolis, Minnesota, Apr. 1993.

[Depalle 93b] Ph. Depalle, G. García, X. Rodet. Analysis of Sound for Additive Synthesis: Tracking of Partials Using Hidden Markov Models, Proceedings of International Computer Music Conference (ICMC'93),Oct. 1993.

[Depalle & Tromp 96] Ph. Depalle, L. Tromp, An improved additive analysis method using parametric modelling of the short-time Fourier transform, Proceedings of International Computer Music Conference (ICMC'96), Clear Water Bay, Hong-Kong, August 1996.

[Doval & Rodet 93] B. Doval, X. Rodet, Fundamental Frequency Estimation and Tracking using Maximum Likelihodd Harmonic Matching and HMM's Proc. IEEE- ICASSP 93, pp. 221-224.

[Doval 94] B. Doval, Estimation de la Fréquence Fondamentale des signaux sonores, PhD. Thesis, Université Paris-6, Paris, 1994.

[Fant 70] G. Fant, Acoustic Theory of Speech Production, Mouton, 1970.

[Fitz & al. 95] K. Fitz, L. Haken, B. Holloway, Lemur - A Tool for Timbre Manipulation, Proc. Int. Comp. Music 1995, Banff, Sept. 1995.

[George & Smith 92] E. B. George, J. T Smith, Analysis-by-Synthesis/Overlapp-Add Sinusoidal Modeling Applied to the Analysis and Synthesis of Musical Tones, J; Audio. Eng. Soc., Vol. 40, No. 6, June 1992.

[Goodwin 96] M. Goodwin, Residual modeling in music analysis-synthesis, Proc IEEE-ICASSP, Atlanta, GA, pp. 1005-1008, May 1996.

[Gribonval & al. 96a] R. Gribonval, E. Bacry, S. Mallat, Ph. Depalle, X. Rodet, Analysis of sound signal with high resolution matching pursuit, Proceedings of the IEEE Conference on Time-Frequency and Time-Scale Analysis (TFTS'96), Paris, France, June 1996.

[Gribonval & al. 96b] R. Gribonval, Ph. Depalle, X. Rodet, E. Bacry, S. Mallat, Sound signal decomposition using a high resolution matching pursuit, Proceedings of International Computer Music Conference (ICMC'96), Clear Water Bay, Hong-Kong, August 1996.

[Griffin & Lim 85] D. W. Griffin, J. S. Lim, A New Model-Based Speech Analysis/Synthesis System, IEEE-ICASPP, 1985, pp. 513-516.

[Kay 88] S. M. Kay, Modern Spectral Estimation: Theory and Apllication, Prentice Hall, 1988.

[Kronland-Martinet 88] R. Kronland-Martinet, The Wavelet Transform for Analysis, Synthesis, and Processing of Speech and Music Sound. in Computer Music Journal, vol 12:4 1988, pp. 11-20.

[Laroche 89a] J. Laroche, Etude d'un système d'analyse et se synthèse utlisant la méthode de Prony, PhD thesis, Télécom Paris, Paris, Oct. 89.

[Laroche & Rodet 89b] J. Laroche, X. Rodet, A new Analysis/Synthesis system of musical signals using Prony's method, Proc. ICMC, Ohio, Nov. 89.

[Laroche 93a] J. Laroche, The use of the Matrix-Pencil method for the spectrum analysis of musical signals, J. Acoust. Soc. America, Vol. 94 No. 4., Oct. 1993.

[Laroche & al. 93b] J. Laroche, Y. Stylianou, E. Moulines, HNM: A simple efficient harmonic model for speech, Proc. IEEE-ASSP Workshop on Applications of Signal Procssing to Audio and Acoustics.

[Liénard 87] J.S. Liénard, Speech Analysis and Reconstruction Using Short-Time Elementary Waveforms, Proc. IEEE-ICASSP 1987, Dallas.

[Maher & Beauchamp 94] R. C. Maher and J. W. Beauchamp, 1994. Fundamental frequency estimation of musical signals using a Two-Way Mismatch procedure, J. Acoust. Soc. Am., Vol. 95, No.4, pp.2254-2263.

[Mallat & Zhang 93] S. Mallat, Z. Zhang, Matching Pursuit with time-frequency dictionaries, IEEE Trans. Signal Process., 41(12):3397-3415, Dec. 1993.

[Masri 96] P. Masri, Computer Modeling of Sound for Transformation and Synthesis of Musical Signal, PhD thesis, University of Bristol, Dec. 1996.

[McAulay, Th. F. Quartieri 86] R.J. McAulay, Th. F. Quartieri, Speech analysis/synthesis based on a sinusoidal representation, IEEE Trans. on Acoust., Speech and Signal Proc., vol ASSP-34, pp. 744-754, 1986.

[McAulay, Quartieri 95] R.J. McAulay, Th. F. Quartieri, Sinusoidal Coding, in Speech Coding and Synthesis, Edited by W. B. Kleijn and K.K. Paliwal, Elsevier Science B.V. 1995.

[McIntyre & Dermott 92] C. M. McIntyre, D. A. Dermott, A New Fine-Frequency Estimation Algorithm Based on Parabolic Regression, IEEE-ICASSP 1992, pp. 541-544.

[Pielemeier & Wakefield 96] W. J. Pielemeier, G.H. Wakefield, A high-resolution time-frequency representation for musical instrument signals, J. Acoust. Soc. Amer., 99(4), 1996.

[Quatieri & McAulay 92] Th. F. Quatieri, R. J. McAulay, Shape Invariant Time-Scale and Pitch Modification of Speech, IEEE Trans. on Signal Processing, Vol. 40 No. 3, March 1992.

[Rabiner 86] L. R. Rabiner, B.-H. Juang. An introduction to Hidden Markov Models. IEEE ASSP Magazine, Jan. 1986.

[Rabiner & Schafer 78] L. R. Rabiner, R. W. Schafer. Digital Processing of Speech Signals,Englewood Cliffs, NJ: Prentice Hall, 1978.

[Ravera & d'Alessandro, 94]B. Ravera, C. d'Alessandro, Double Frequency and Time-Frequency Analyses of Modulated Speech Noises, Signal Processing VII: Théories et Applications, Edited by M. Holt, C. Cowan, P. Grant, W. Sandham, 1994.

[Risset & Mathews] J.C. Risset, M.V. Mathews, Analysis of musical-instrument tones, Physics Today, 22(2):23-30, Feb. 1969.

[Rodet 80] X. Rodet , Time-domain formant-wave-function synthesis, J.C. Simon ed., 1980, Spoken Language Generatoion and Processing, D. Reidel Publishing Company, Dordrecht, Holland.

[Rodet & al. 87] X. Rodet, Ph. Depalle, G. Poirot, Speech Analysis and Synthesis Methods Based on Spectral Envelopes and Voiced/Unvoiced Functions, European Conference on Speech Tech., Edinburgh, U.K., Sept. 87, pp. 155-158.

[Rodet & al. 88] X. Rodet, Ph. Depalle, G. Poirot, Diphone Sound Synthesis based on Spectral Envelopes and Harmonic/Noise Excitation Functions, ICMC, Kohln, Germany, Sept. 1988.

[Rodet & Depalle 92] X. Rodet, Ph. Depalle. A new additive synthesis method using inverse Fourier transform and spectral envelopes. Proc. of ICMC, San Jose, California, Oct. 1992.

[Rodet & Lefèvre 96] X. Rodet, A. Lefèvre, Macintosh graphical interface and improvements to generalised Diphone control and synthesis, ICMC'96, Hong Kong, Aug. 1996.

[Serra 89] X. Serra. A system for sound analysis/transformation/synthesis based on a deterministic plus stochastic decomposition. Philosophy Dissertation, Stanford University, Oct. 1989.

[Smith & Gossett 84]J.O. Smith and P. Gossett, A Flexible Sampling-Rate Conversion Method, Proc. IEEE ICASSP, vol. 2 , pp. 19.4.1-19.4.2, San Diego, March 1984.

____________________________
Server © IRCAM-CGP, 1996-2008 - file updated on .

____________________________
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .