
Tous droits réservés pour tous pays. All rights reserved.
 | Serveur © IRCAM - CENTRE POMPIDOU 1996-2005. Tous droits réservés pour tous pays. All rights reserved. |
Rapport Ircam 30/80, 1980
Copyright © Ircam - Centre Georges-Pompidou 1980
Résumé
Le but de ce rapport, comprenant une brève réflexion sur l'utilisation musicale de l 'aléatoire, est de donner à des compositeurs une connaissance pratique de la théorie des probabilités, ainsi que des formules ou logiciels pour la génération d'événements aléatoires obéissant à diverses lois de probabilité.
En 1954, Xenakis énonça deux critiques à l'encontre de la composition sérielle, qui était alors indéniablement la technique la plus répandue dans l'avant-garde : « ... le système sériel est remis en question en ses deux bases qui contiennent en germe leur destruction et leur dépassement propres » ([2], p.120).
Sa première critique est d'ordre intrinsèque, est une vue généralisante : les techniques sérielles sont un cas particulier du vaste domaine du calcul combinatoire, et, en outre, le sérialisme est demeuré engagé dans son héritage historique alors que, particulièrement par l'électroacoustique, de nouveaux horizons étaient ouverts : « Pourquoi douze et pas treize ou n sons ? Pourquoi pas la continuité du spectre des fréquences ? Du spectre des timbres ? Du spectre des intensités et des durées ? » (ibid.).
Sa seconde remarque relève une contradiction des processus sériels par rapport à leur résultat sonore : « La complexité énorme empêche à l'audition de suivre l'enchevêtrement des lignes et a comme effet macroscopique une dispersion irraisonnée et fortuite des sons sur toute l'étendue du spectre sonore » (ibid.).
Et il concluait : « L'effet macroscopique pourra donc être contrôlé par la moyenne des mouvements des n objets choisis par nous. Il en résulte l'introduction de la notion de probabilité qui implique d'ailleurs dans ce cas précis le calcul combinatoire » (ibid.). Cette conclusion est ainsi une généralisation, introduisant le concept du contrôle global d'événements sonores complexes, plutôt que leur élaboration analytique et mécanique, exactement comme, en sciences, les méthodes statistiques sont un outil de préhension globale de phénomènes analytiquement excessivement complexes ; ce qui est bien conforme à notre conception intuitive du hasard. Mais il faut ajouter d'autre part que Xenakis portait en lui-même certaines intuitions musicales de masses sonores, probablement antérieures à leur justification rationnelle ([1], pp.19-20).
Au cours d'une longue pratique des techniques sérielles, Gottfried Michael Koenig arrive à la même conclusion : « The greater the extent to which parameters adhere to certain arrangements and the greater the extent to which musical meaning is to depend on the perception of these arrangements, the more unpredictaable, « random », are the effects of one parameter on the other : the various characteristics coalesce to « sounds » whose order is unequivocally defined neither by the course of an individual parameter nor by the polyphony of all of them » ([4], p.22). L'idéal de la composition systématique -- « un formalisme décrivant complètement, dans [les] deux directions [des événements passés et futurs], chaque instant de l'oeuvre » ([4], p.9) -- se déjoue lui-même.
Techniquement, d'ailleurs, les déterminismes complexes débouchent sur un excès de possibilités, un labyrinthe d'ambiguïtés. D'où, par exemple, chez Koenig, les concepts de forme potentielle et de forme effective (actual form) : une pièce ne réalise pas nécessairement toutes les virtualités offertes par un système, mais elles sont disponibles : au compositeur de choisir (cf. [4], pp.65-66).
Lorsque le compositeur ne souhaite pas choisir jusqu'au bout, il en arrive à ce que les compositeurs sériels ont expérimenté sous le vocable d'aléatoire, négotiant un compromis entre leur conception de la composition musicale et les idées de Cage : soit au niveau de certaines sections d'une pièce, où il fournit simplement un matériau de base, sur lequel une solution ad hoc devra être improvisée, soit au niveau de la macrostructure, où il laisse le choix de parcours, parmi certains modules musicaux précomposés. En tous cas, la question fondamentale du choix n'est que différée, mais l'on gagne sur le plan de la généralité de l'oeuvre, de la combinaison attrayante de perspectives variées sur le paysage sonore (Murray Schafer) accessible à la pièce.
Mais cet aléatoire n'est pas du même ordre que l'aléatoire en tant que principe métaphysique, que technique impersonnelle destinée à laisser les sons et les silences être, tout simplement, que Cage pratiquait déjà auparavant (cf. [6]) .
Pour ainsi dire, Cage souhaite affranchir les sons de la musique et des musiciens, tandis que Xenakis « s'inscrit volontairement non dans la tradition, mais dans l'histoire de son art » ([7], p.9-35). Une fois acquis les concepts de paramètres musicaux (hérité de Webern) et de leur indépendance (cf.[8], p. 17), généralisés par l'intermédiare de Messiaen, l'utilisation de la théorie des probabilités est une technique apte à concilier la recherche de nouvelles sonorités, masses sonores, etc., entreprise par la musique sérielle, l'indépendance des paramètres et la volonté -- toujours présente -- du compositeur « classique » de dominer personnellement son oeuvre : « ... la seule issue qui respecte à la fois la liberté totale de chaque élément et la prévisibilité globale » ([7], p. 237).
Mais la musique stochastique est plus qu'une solution technique ; elle est le fruit d'une longue tradition rationaliste. En effet, la théorie des probabilités est un formalisme mathématique basé sur une question fondamentale : que peut-il se produire dans notre univers, dans telle ou telle situation ? Étant donnés certains postulats (homogénéité ou non, différentes notions de moyennes, etc.), la théorie des probabilités offre des outils de choix adaptés aux hypothèses de départ -- et même déduits d'elles ; et dans le choix réside notre conception de la création artistique.
Dans les pages qui suivent, vous trouverez des méthodes de génération de variables aléatoires, qui ne sont pas nouvelles, originales ou exclusives en elles-mêmes : vous pouvez en consulter d'autres, par exemple, dans [11] ou [12], renvoyant eux-mêmes à une bibliographie considérable. Mais ce rapport devrait posséder au moins le mérite d'avoir été rédigé par un musicien, avec des intentions musicales, finalement, et de rassembler une panoplie à cet effet.
Mon intention est de donner à des musiciens encore moins
mathématiciens que moi, des moyens utiles pour atteindre des buts
qu'ils recherchent probablement, et particulièrement de soustraire
tant d'applications compositionnelles de l'informatique à
l'utilisation indigente et sempiternelle de valeurs aléatoires
tirées directement de cette omnipotente « boîte noire » des
ordinateurs : le générateur aléatoire à distribution continue
uniforme.
Dans des cas simples, les probabilités sont assez faciles à évaluer.
Par exemple, la probabilité d'obtenir un nombre impair lors du jet
d'un dé est 3/6 (l'événement comprend trois résultats sur un total
de six possibilités). Mais si l'on joue avec deux dés, il faut déjà
réfléchir... Voici un problème fameux (Les boîtes d'allumettes de Banach, [22a],
p.166) : un fumeur possède deux boîtes de N allumettes
chacune ; lorsqu'il allume sa pipe, il choisit une boîte au
hasard ; lorsqu'il retirera la dernière allumette de l'une des
boîtes, quelle est la probabilité que l'autre en contienne encore
x ?... Il est souvent nécessaire de recourir à des calculs
combinatoires assez complexes, simplement pour estimer « de combien
de façons l'événement peut se produire », et pour déterminer « combien
d'événements comporte l'ensemble fondamental ».
Cette approche intuitive de la probabilité suffira pour notre
propos, et sera complétée au besoin. Sauf à titre d'exemples
illustrant quelques notions de base, nous ne traiterons pas ici de
situations ou de mécanismes réels ; nous allons plutôt décrire
des algorithmes -- des machines imaginaires -- se conformant à
certains schèmes classiques de la théorie des probabilités. Pour
prendre connaissance de définitions complètes et formalisées de la
probabilité et de l'analyse combinatoire, reportez-vous à [21],
chapitres 1 et 2, ou à [22a], chapitres 1 et 2. Des introductions
simples à la théorie des probabilités peuvent être consultées dans
des manuels scolaires ; [20] est très clair et complet.
Des définitions de la probabilité et de la variable aléatoire, il
découle que la somme des probabilités de toutes les valeurs
éventuellesd'une variable aléatoire égale 1 : pour s couvrant
l'ensemble des valeurs possibles de X,
Nous pouvons à tout le moins utiliser cette terminologie dans des
énoncés comme
Encore une fois, ce concept de fonction de répartition peut
sembler superflu, mais il s'avérera fondamental pour nos
algorithmes. Une fonction de répartition peut être représentée par
un graphe : pour l'exemple de l'urne, la figure 2 illustre
clairement la définition cumulative de F(x).
Pour explorer la théorie complète des variables aléatoires
discrètes, voyez [22a] ou les chapitres adéquats de [21].
[19] constitue une excellente introduction aux probabilités discrètes,
et facilement lisible. Les manuels scolaires se limitent souvent
aux variables discrètes.
Dans le cas de variables discrètes, l'équation (c) (2.3,
ci-dessus) énonçait que la somme des probabilités de tous les
événements de l'ensemble fondamental E doit égaler 1.
Graphiquement, cela signifie que la somme des « bâtons » de
l'histogramme doit correspondre à une unité de l'échelle verticale
du graphe. Dans le cas de variables continues, c'est la surface
délimitée par la fonction de probabilité et l'axe horizontal qui
doit égaler 1. Cela peut être saisi intuitivement si l'on imagine
cette surface comme remplie d'une infinité de « bâtons » verticaux
correspondant à l'infinité des valeurs réelles que peut assumer la
variable aléatoire : voyez la surface hachurée de la figure 4.
Ainsi, lorsque l'on passe des variables discrètes aux variables continues, on substitue
l'intégrale de l'équation (e) à la somme de l'équation (c) :
Dans le cas de variables discrètes cependant, la probabilité des
événements correspond bien sur l'histogramme à des « bâtons » de
hauteur appropriée (figure 1). Mais pour des variables continues,
à cause de l'infinité des valeurs éventuelles, il nous faut
renoncer à l'idée d'une probabilité associée à un événement
précis ; en effet, cette probabilité serait zéro :
Pour vous initier au calcul différentiel et intégral, et vous
familiariser avec ces transitions du domaine discontinu à la
continuité, vous pouvez consulter [23] avec profit,
ou [24] pour un exposé historique et philosophique.
[22b] et [21] exposent une théorie complète
des variables aléatoires continues.
Il nous reste cependant à étudier un exemple qui sera d'importance
primordiale pour notre propos.
D'une collection de hauteurs discrètes, se dégage une terminologie
destinée à qualifier diverses sensations (« grave » et « aigu » sont
les termes les plus usités), et découle la notion de différences
de hauteur -- de distances entre des hauteurs --, ainsi que
l'aptitude à comparer ces différences en termes quantitatifs de
taille. Pour les besoins de ces comparaisons, l'on est amené à
effectuer certaines opérations mentales : abstraire les
différences de hauteur des successions chronologiques de stimuli
qui les incarnent, déplacer mentalement des différences entre
diverses paires de hauteurs plus aiguës ou plus graves, inverser
le sens de différences -- de « vers l'aigu » à « vers le grave » ou
vice-versa --, utiliser éventuellement des réitérations d'une
petite différence unitaire afin d'en mesurer de plus grandes, etc.
Par ces opérations, l'on pourrait arriver à ordonner totalement
les sensations de hauteur, puisque l'on serait en mesure d'évaluer
la taille relative et le sens de différences entre tout couple de
hauteurs. De surcroît, l'on pourrait définir axiomatiquement des
échelles tempérées de hauteurs, à partir seulement d'une hauteur
de référence fixe et d'une différence unitaire quelconque, ainsi
que l'a souligné Xenakis d'après l'axiomatique des nombres de
Peano ([2], p.61).
Bien entendu, les musiciens prennent pour acquise cette structure
totalement ordonnée des hauteurs, et ils ont conquis depuis
longtemps une remarquable faculté de manipulation des intervalles
de hauteur. Si l'on définit ainsi l'« addition » de deux intervalles
(symbolisée par
) : « faire coïncider à la même
hauteur le point d'arrivée du premier et le point de départ du
second », et si l'on considère le résultat de cette opération comme
étant l'intervalle allant du point de départ du premier au point
d'arrivée du second, on peut démontrer que, avec cette opération
musicale banale, les intervalles de hauteur possèdent la structure
mathématique d'un groupe commutatif (cf. [25], chapitres 1 et 2,
pour des définitions de groupes) ; en effet, les cinq conditions requises sont réalisées :
Si l'on quitte le domaine de la perception pour celui des stimuli
physiques, si l'on parle en termes de fréquence au lieu de
hauteur, l'extension aux nombres réels est également
vraisemblable. Les échelles non-tempérées sont édifiées dans un
groupe de rapports rationnels avec la multiplication comme
opération, et les gammes tempérées peuvent être considérées comme
utilisant des rapports irrationnels -- impliquant par exemple des
racines de deux si elles possèdent un modulo d'octave -- ; de
là aussi, l'extension aux nombres réels découle aisément.
On comble ainsi graduellement les intervalles séparant les entiers
et les rationnels, pour atteindre la continuité : « Il suit de
la division actuelle que, dans une partie de la matière, si petite
qu'elle soit, il y a comme un monde consistant en créatures
innombrables » (Leibnitz, cité dans [24], p.55). Par la subdivision
spéculative, on atteint des intervalles plus fins que notre seuil
de différentiation, s'évanouissant dans la continuité. Mais
peut-être, paradoxalement, peut-on considérer aussi bien la
continuité comme donnée, et voir dans les échelles traditionnelles
des systèmes de points de repère jalonnés empiriquement afin de
satisfaire nos besoins de techniques opératoires et de
hiérarchies, de normes comparatives « ... un ensemble continu n'est
pas le résultat des parties en lesquelles il est divisible, mais
il en est au contraire indépendant, et, par suite, le fait qu'il
nous est donné comme tout n'implique nullement l'existence
actuelle de ces parties » ([24], p.60).
En tous cas, on peut prétendre que les intervalles, et les
hauteurs elles-mêmes en tant qu'incarnations d'intervalles, sont
isomorphes aux nombres réels, et donc à une droite isomorphe à ces
derniers : ce paramètre musical est totalement ordonné et
théoriquement continu. D'autres paramètres possèdent la même
structure -- intensités, densités, etc. L'on doit cependant
excepter les paramètres de définition qualitative, bien entendu,
tel le timbre. Mais peut-être pourra-t-on éventuellement, par la
synthèse numérique-analogique, réduire cette qualité complexe
appelée « timbre » à une série de paramètres quantifiables -- et dès
à présent, certaines échelles restreintes de timbres sont
concevables. Le temps lui-même, le temps métrique, de par les
opérations mentales auxquelles nous pouvons le soumettre, révèle
cette même structure profondément enracinée dans notre
fonctionnement psychique, ainsi que l'a montré Piaget ([9],
chapitre Il §5 particulièrement, où est développée la notion de
« groupement » logique, pp.74-83). Léonard de Vinci avait saisi une
grande part de tout cela dans une note datant d'environ 1500, que
je cite volontiers. « Le point, si on lui applique les termes
réservés au temps, se doit comparer à l'instant, et la ligne à la
longueur d'une grande durée de temps. Et tout comme les points
constituent le commencement et la fin de ladite ligne, ainsi les
instants forment le principe et le terme d'une certaine portion de
temps donné. Et si une ligne est divisible à l'infini, il n'est
pas impossible qu'une portion de temps le soit aussi. Et si les
parties divisées de la ligne peuvent offrir une certaine
proportion entre elles, il en est de même pour les parties du
temps » (Carnets, E. Mac Curdy et L. Servicen , vol. I, Paris,
Gallimard, 1942, p. 76).
Ces justifications peuvent aujourd'hui sembler superflues, mais il
n'en est pas ainsi depuis longtemps dans notre tradition musicale.
Pensez, par exemple, en 1916, aux explications très laborieuses de
Russolo sur ses instruments (intonarumori) capables d"un système
enharmonique complet où chaque ton a toutes les mutations possibles en se subdivisant en
un nombre indéfini de fractions ([10], p .83, c'est moi qui
souligne) ; il introduit finalement, à propos de questions de
notation, une notion assez vague de continuité dynamique (ibid., p. 87)
-- c'est à dire continuité de hauteur. Ce n'est que relativement
récemment que de telles notions ont été effectivement adoptées par
la pratique musicale, et elles sont peut-être maintenant
définitivement acquises.
Dans les pages qui suivent, nous nous tiendrons donc sur le terrain,
musicalement assez abstrait, du groupe des nombres réels avec
l'addition comme loi de composition -- puisque nous n'aurons pas de
raison de nous aventurer hors du domaine perceptif. Mais, étant
établie la correspondance avec les paramètres musicaux, ou
caractéristique sonores, la musique sera toujours virtuellement
présente, et les applications pratiques seront de préférence
laissées à votre propre imagination.
Mais notre but est à l'opposé de cette démarche : nous désirons
synthétiser des populations conformes à des distributions de
probabilité. Pour ce faire, il nous faudra transformer les formules
de la théorie des probabilités de telle sorte que la variable
aléatoire soit une fonction de sa fonction de répartition -- les
retourner sens dessus dessous, pour ainsi dire ; ceci sera
élucidé par la suite. Ce qui nous intéresse, c'est de partir de la
définition d'une population -- d'un histogramme, finalement, choisi
pour des raisons formelles, esthétiques, ou musicales quelconques --
afin de modeler une certaine caractéristique sonore, puis de faire
la synthèse de valeurs s'y ajustant.
Mais rien ne garantit que notre population synthétique, qui sera
composée d'un nombre limité de valeurs aléatoires, s'ajustera avec
précision et élégance à l'histogramme désiré, et l'incarnera d'une
manière idéale. Des valeurs aléatoires sont aléatoires, quoiqu'il en
soit, et ne suivent pas nécessairement avec docilité les intentions
de notre imagination. La conformité d'une population à une
distribution de probabilité donnée ne peut se réaliser que pour un
très grand nombre de valeurs échantillons. Ce principe est établi
sous le nom de loi faible des grands nombres : « Si dans une
épreuve [...] la probabilité d'un événement [...] est p, et si
l'on répète l'épreuve un grand nombre de fois dans des conditions
identiques [...], le rapport entre le nombre de fois que se
produit l'événement et le nombre total d'épreuves -- c'est à dire
la fréquence f de l'événement -- tend à se rapprocher de plus en plus
de la probabilité p. Plus précisément, si le nombre d'épreuves est
suffisamment grand, il devient tout à fait improbable que l'écart
entre f et p dépasse une valeur quelconque, si petite soit-elle,
donnée à l'avance » ([18], pp.28-29).
Ainsi, il faut être prêt à accepter des valeurs, ou des
successions de valeurs aléatoires « étranges », ou peut-être à
choisir, parmi quelques populations, celle qui incarne le plus
fidèlement notre Idée platonicienne de la distribution. « This
brings up a philosophical point. Do we really want genuine random
numbers, or do we want a set of homogenized, guaranteed, and
certified numbers whose effect is random but at the same time we
do not run the risk of the fluctuations of a truly random
source ? We usually find that we want to get the security of
a large number of eamples by taking [as few] as we can » [13]
p.143).
Dans la suite de ce rapport, nous allons appliquer toutes ces
notions en continuant d'utiliser le même symbolisme :
Lorsqu'un canon consiste en l'application d'une unique formule,
seule cette dernière sera donnée. Lorsque des algorithmes complets
seront nécessaires, ils seront donnés en FORTRAN -- un langage de
procédures explicites très répandu ou aisément traduisible.
Afin de choisir un événement, l'on pourrait utiliser la méthode
générale décrite ci-dessous pour d'autres variables aléatoires
discrètes, mais, toutes les probabilités étant ici égales, le cas
est simple, et l'on peut faire directement de X une fonction
linéaire de U :
L'algorithme suivant effectue cette tâche :
Il n'est peut-être pas nécessaire de mettre au point un canon
binomial, puisque l'on peut saisir ce problème par des choix
directs, sans avoir recours à la distribution analytique. Si l'on
avait besoin d'un tel algorithme, il serait semblable à celui de
la distribution de Poisson (3 .3 .3, ci-dessous) :
préparation, d'abord, d'une table cumulative F(x) au moyen de la
formule ci-dessus, puis recours à un us pour désigner le xs
résultant. L'on aurait alors décidé, par exemple, que parmi les n
prochains événements, il y aurait xs succès, et bien entendu n-xs
occurrences de l'autre alternative. Il serait aussi possible
d'utiliser le canon de Poisson directement, puisque cette dernière
distribution constitue, dans certaines conditions, une
approximation de la distribution binomiale (voir 3 .3 .3,
ci-dessous). Un histogramme de la variable aléatoire B(50,5%) est
représenté à la figure 10.
Lorsque n devient grand et que p n'est pas petit, de telle sorte que
les produits np et n(1-p) sont quelque peu supérieurs à 15 ou
20 -- avec de meilleures approximations si p est proche de 0.5 --,
on peut démontrer que la distribution binomiale équivaut assez
bien à une distribution de Gauss-Laplace (voir 4 .4 .1,
ci-dessous) de moyenne np et d'écart type
([21], pp. 310-316, et [22a], chapitre VII).
Dans de tels cas, l'on pourrait utiliser encore plus aisément la canon Gauss-Laplace décrit
ci-dessous, et arrondir le résultat à l'entier le plus proche.
Vous trouverez dans [21], pp.445-449, d'intéressantes comparaisons
graphiques entre des histogrammes des lois
binomiale et de Gauss-Laplace. Une bonne introduction à cette
famille de distributions -- binomiale, Gauss-Laplace et Poisson --
peut être consultée dans [18], chapitre III. Traitant
exclusivement de variables aléatoires discrètes, [19] approche
aussi la distribution de Gauss-Laplace à travers la binomiale.
Quoi qu'il en soit, la distribution de Poisson incarne bien, comme
la binomiale, un point de vue analytique sur une série de tirages
bernoulliens : elle décrit la probabilité d'obtenir x succès
dans un grand nombre de tirages, lorsque la densité moyenne de
succès est
Remarquez que n, le nombre de tirages, est absent de la formule.
La figure 11 montre un histogramme de la distribution de Poisson
de densité 2.5.
Nous présentons un algorithme pour cette distribution parce
qu'elle a acquis une certaine notoriété par l'usage qu'en
a fait Xenakis ([1], pp.35sq.) en tant qu'approche analytique de
phénomènes se déroulant dans le temps : dans de
tels cas, la distribution de Poisson concerne la probabilité de
trouver x points par unité de temps sur un axe
chronologique, lorsque la densité moyenne de points par unité est
(suffisamment petite), et lorsque la distribution de ces points se conforme à une distribution exponentielle
homogène (voir 4 .3 .2, ci-dessous). Tout se passe
comme si, d'un point de vue binomial, l'on considérait le temps
comme une succession de très courts intervalles :
un succès serait alors la présence d'un point occupant un
intervalle. Notre famille binomiale-Gauss-Laplace-Poisson,
comportant aussi une distribution binomiale négative que
nous n'étudierons pas ici (cf.[21], pp.321sq., et
[22a], pp.164sq.), se trouve donc de surcroît en relation avec
les distributions gamma (4 .3 .3, ci-dessous), dont
l'exponentielle est un cas particulier (cf. [21], pp.332-337 et
354-356, ou [22b], pp.11-15 et passim) : « ...the
remarkable fact that there exist a few distributions of great
universality which occur in a surprisingly great variety of
problems. The three principal distributions, with ramifications
throughout probability theory, are the binomial
distribution, the [Gauss-Laplace] distribution [...], and the
Poisson distribution » ([22a], p.156).
L'algorithme suivant est conçu pour gérer plusieurs distributions
de Poisson de paramètres indépendants.
Un appel à POINIT comprend les paramètres suivants :
Cette étape préliminaire étant exécutée, les appels destinés à
obtenir effectivement des valeurs aléatoires doivent utiliser
l'ENTRY POISSO(I,N,NBR,TAB,ITOT,NMAX). L'algorithme se procure
alors un us en appelant RAN(0), et l'utilise pour dèsigner un xs.
Un paramètre particulier est inclus dans l'appel :
NBR, qui transmet xs, le résultat --« Il y aura NBR événements »
Tous les autres paramètres sont comme ci-dessus.
BOUL : le nom du vecteur déclaré dans le programme appelant,
contenant la liste des différentes alternatives :
La distribution multinomiale constitue une approche analytique de
ce problème ([21], pp.337sq., et [22a],
pp.167sq.). Un algorithme multinomial serait très lourd, puisqu'il devrait manipuler des
vecteurs entiers d'événements : sur n tirages, il devrait y avoir xs1
événements x1, xs2
événements x2, etc... Cette méthode se
révélerait passablement inefficace, comparée à la simplicité de la
synthèse directe des événements.
Il existe une approche analytique de ce problème : la
distribution hypergéométrique ([21], pp.316sq., et [22a],
pp.43-47), qui serait cependant peu utile ici. Une méthode
synthétique pourrait consister à modifier l'algorithme ALTERN,
ci-dessus, de manière à ce qu'il ajuste la liste PROB de
probabilités après chacun des tirages, ou de confier cette tâche au
programme appelant. Mais puisque vraisemblablement l'ensemble
fondamental sera d'un nombre restreint d'événements, il est plus
pratique d'utiliser l'algorithme de permutation ci-dessous (tiré de
[5], pp.70-73), en considérant le vecteur permuté, item par item,
comme une série de tirages exhaustifs.
2. Définitions préliminaires
2.1 Probabilité
Une probabilité est une fraction concernant un ensemble fondamental
E : l'ensemble de tous les événements possibles dans une
situation donnée. Les événements sont en quelque sorte les résultats
éventuels d'une expérience précise : les jeux que peuvent avoir
en main les partenaires d'une partie de cartes, les états d'une
machine, les couleurs de voitures défilant dans une rue, les quatre-vingt-huit
touches d'un piano, etc... La probabilité d'un événement
spécifique inclus dans l'ensemble fondamental (sous-ensemble de
celui-ci) est
La valeur de cette fraction doit vraisemblablement se situer entre 0
et 1 car :
(a)
Une probabilité est ainsi un rapport quantitatif entre deux
ensembles d'événements : l'ensemble fondamental et un
sous-ensemble de ce dernier, mesurant la proportion d'un événement
spécifique incluse dans l'ensemble fondamental. Plus grande est la
probabilité d'un événement, plus il est vraisemblable qu'il se
produise effectivement -- pourvu que quelque chose se produise !
2.2 Variable aléatoire
Une variable aléatoire (symbolisée ci-après par X) est une variable
qui assume aléatoirement une valeur spécifique (symbolisée par Xs)
correspondant à un événement spécifique inclus dans l'ensemble
fondamental. Ainsi, dans la situation où l'ensemble fondamental est
une urne renfermant douze boules colorées : trois rouges, cinq
bleues et quatre blanches, la variable aléatoire X est la couleur
d'une boule tirée au hasard. Elle peut assumer l'une des trois
valeurs (rouge, bleue, blanche), qui peuvent être abstraites et
ordonnées sous la forme symbolique {x1, x2, x3}.
Nous connaissons en outre les probabilités de ces valeurs :
ce qui se lit : « la probabilité que X égale x1 égale... » etc.
(b)
Dans l'exemple ci-dessus :
2.3 Fonction de probabilité
Le concept de variable aléatoire nous conduit à celui de la
probabilité en tant que fonction de x : pour s couvrant
l'ensemble des valeurs possibles de X, la fonction
est la fonction de probabilité de la variable aléatoire X. Nous venons
simplement d'affirmer que P{X= xs} est fonction de xs.
L'utilité de cette affirmation n'apparaît peut-être pas encore, dans
des cas tels que celui de l'urne du paragraphe
précédent, mais elle se révélera d'importance capitale par la suite,
lorsque nous aurons recours à d'authentiques
fonctions de x pour décrire des fonctions de probabilité -- ou
densités --, particulièrement dans le cas de variables
aléatoires continues (2.6, ci-dessous).
équivalent aux équations (a) ci-dessus, et
(c)
équivalent à (b) ci-dessus.
Une fonction de probabilité peut être visualisée sous la forme d'un
graphe en deux dimensions, comme toute fonction ; dans le cas
de probabilités, un tel graphe s'appelle un histogramme. La figure 1
représente l'histogramme de notre urne du paragraphe 2.2 ;
chaque « bâton » vertical est de hauteur proportionnelle à la
probabilité qu'il illustre.
2.4 Fonction de répartition
La fonction de probabilité f(x) doit être bien distinguée de la
fonction de répartition F(x), définie par
(d)
La somme des probabilités de tous les événements ordonnés n'excédant
pas xs. Cela revient à dire que F(xs) est la probabilité que X
assume l'une des valeurs
cet ensemble constituant aussi un sous-ensemble de E. L'équation (c)
de 2.3 énonçait le cas particulier de
F(xs=1) parce que s couvrait tout l'ensemble fondamental E. Mais,
dans le cas de notre urne, par exemple, on aura
deux fois sur trois, X sera x1, ou x2 (la boule ne sera pas
blanche).
2.5 Variable aléatoire discrète
Une variable aléatoire X est dite discrète si elle peut assumer
des valeurs parmi un ensemble ordonné et fini de possibilités. À
date, nous n'avons traité que de variables discrètes, afin de
jeter des bases solides avant d'aborder le paragraphe suivant sur
les variables continues. Concrètement, des variables discrètes
sont celles qui n'assument que des valeurs absolument distinctes,
comme x1, x2, ou x3, séparées par
de nettes solutions de continuité. Cela se traduit par des histogrammes constitués de
« bâtons » verticaux -- tel celui de la figure 1 --, et des
fonctions de répartition en escaliers -- comme sur la figure 2.
2.6 Variable aléatoire continue
Une variable aléatoire X est continue lorsque sa fonction de
répartition F(x) est continue. Ceci implique que sa
fonction de probabilité f(x) -- bien qu'elle puisse comprendre des
discontinuités -- n'est pas, comme dans le cas
d'une variable discrète, une énumération de valeurs distinctes (f(x1), f(x2), ... )
qui se traduit par une F(x) discontinue (en escalier), mais une f(x) définie sur un intervalle
de valeurs réelles pouvant être assuméee par X. La
figure 3 représente l'histogramme d'une fonction de probabilité
continue (la distribution normale) : cette variable
aléatoire peut assumer une infinité de valeurs : n'importe
quel nombre réel.
(e)
et, de façon analogue, la définition d'une fonction de répartition
continue est
(f)
au lieu de (d) (2.4, ci-dessus). La figure 4
illustre cette notion.
Donc, la « hauteur » de f(xs) n'est pas telle quelle la probabilité
de xs. Nous devons nous contenter de connaître la probabilité que
X assume une valeur comprise dans un certain intervalle appelé
différentielle (dx), qui peut être aussi ténu que l'on veut, mais
non nul. Ainsi, la fonction de probabilité d'une variable continue
X est f(x), mais la probabilité d'un xs spécifique est 0 :
Il nous faut introduire une multiplication par la différentielle
afin de manipuler une probabilité « tangible » :
La figure 5 illustre ceci : la surface sous f(xs) est nulle
(les points mathématiques xs et f(xs) n'ont aucune « largeur »)
et l'on doit approximer
au moyen d'un petit rectangle différentiel de largeur dx. Avec cette
précaution mathématique, l'histogramme d'une variable continue
peut se lire directement : plus grande est f(xs), plus
est probable.
2.6.1 La distribution continue uniforme
La variable continue uniforme, pour laquelle nous utiliserons le
symbole particulier U, est une variable aléatoire qui peut assumer
équiprobablement n'importe quelle valeur réelle u entre zéro et
un : dans l'intervalle [0,1]. Elle est définie par
La figure 6 représente son histogramme. L'aire rectangulaire
délimitée par f(u) et l'axe des u mesure 1 par 1 : elle est
donc égale à 1, conformément à l'équation
(g)
Nous ferons un usage constant de ce fait dans nos canons, puisque
la variable continue uniforme U (voir 4. 1, ci-dessous, pour de
plus amples détails) est donnée par la « générateur aléatoire »
standard des ordinateurs, sous des appellations comme RAN, RANF,
RAND, etc. ; et tous nos algorithmes y auront recours.
2.7 Structure continue des paramètres musicaux
Afin de nous assurer de la structure des paramètres musicaux sur
lesquels nous nous proposons d'agir, étudions l'exemple de la
hauteur, et, à titre d'hypothèse de départ, considérons la simple
capacité de percevoir des hauteurs distinctes, dont nous pouvons
gratifier toute oreille « normale ».
Cependant, dans le cas le plus général, ce groupe des intervalles
de sensations de hauteur possède la même structure, est isomorphe
à celui des nombres rationnels avec l'addition arithmétique comme
opération -- loi de composition. Les musiques anciennes et
non-tempérées, basées sur des échelles diverses, manipulaient
ainsi des nombres rationnels ; et l'on ne peut que gagner sur
le plan de la généralité théorique en étendant ce domaine à celui
de l'ensemble des nombres réels, dont les rationnels sont un
sous-ensemble, à tous les intervalles de hauteur possibles. Si,
comme dans notre cas, la tradition nous met en présence de gammes
tempérées, l'extension se ferait de façon analogue : on peut
étiqueter les intervalles au moyen du nombre d'intervalles
unitaires (demi-tons, par ex.) qu'ils représentent en taille et en
sens. Dans ce cas l'on forme un groupe isomorphe à celui des
entiers avec l'opération addition (un sous-groupe du précédent),
à partir duquel on peut gagner de proche en proche les nombres
rationnels, irrationnels et, finalement, réels, tout aussi bien.
2.8 Canons
In the final analysis, randomness,
La théorie des probabilités trouve normalement son utilisation
pratique dans les statistiques : on peut analyser les résultats
d'expériences, de sondages, vérifier s'ils se conforment à une
distribution quelconque, si des configurations anormales proviennent
de failles dans le dispositif expérimental, etc. : les
distributions de probabilité sont étudiées en tant que modèles
théoriques de population -- des événements ou des séries d'événements
"naturels", aussi bien de la vie quotidienne que d'expériences
scientifiques complexes.
like beauty, is in the eye of the beholder.
R. W. Hamming
3 Lois de probabilité discrètes
3.1 Distribution uniforme discrète
Cette distribution concerne n événements équiprobables. Elle
équivaut au choix aléatoire de l'un de n nombres entiers entre
deux limites J1 et J2
La fonction de probabilité est constante pour tous les événements
possibles :
où n=J2-J2+1, c'est-à-dire le nombre d'entiers inclus dans
l'ensemble fondamental. Un histogramme est représenté à la figure 8.
Nous ferons appel à l'arithmétique entière de l'ordinateur pour
tronquer ce X réel en un entier. L'équation précédente
pourrait être paraphrasée ainsi : étant donné un us réel dans
l'intervalle [0, 1], nous « étirons », au moyen d'une
multiplication par n, cet intervalle à [0,n], puis, par
l'addition de J1, nous le translatons à [J1, n+J1]. Une fois
tronqué, le résultat sera un entier dans [J2, J2].
FUNCTION INRECT(J1,J2)
U=RAN(0)
N=J2-J1+1
X=N*U+J1
INRECT=IFIX(X)
RETURN
END
3.2 Méthode générale pour l'obtention de distributions discrètes
Lorsque les probabilités affectées à n événements discrets ne sont
pas égales, il est nécessaire de recourir à une table cumulative
de probabilités. Cette table contient les n valeurs suivantes :
équivalentes à
............................................................
Puisque F(x1)>0 et F(xn)=1, toutes ces valeurs peuvent être
assimilées à des points subdivisant un segment réel [0,1] en plus
petits segments égaux aux différentes probabilités mises en jeu
(figure 9). Après l'obtention d'un us, à partir du canon U, il
nous suffit d'examiner à l'intérieur de quel segment il est
« tombé » pour désigner le xs choisi :
.........
Dans les canons qui suivent, une méthode simple sera
utilisée : on fera un balayage de F(x), à partir de F(x1)
vers F(xn), jusqu'à ce que l'on arrive au xs désigné. D'autres
algorithmes pour effectuer cette recherche sont décrits dans [11], pp.101-102.
.........................................
3.3 Quelques distributions discrètes
3.3.1 Choix entre deux alternatives
L'algorithme suivant effectue un choix entre deux alternatives de
probabilités données (vraisemblablement différentes). Il suffit de
spécifier P{X=x1} puisque P{X=x2}=1-P{X=x1}.
Les paramètres suivants sont transmis par la programme appelant :
Une version spéciale de ce canon peut être utile pour effectuer un
choix entre +1 et -1 en tant que signes équiprobables. De tels cas
sont fréquents dans [1], Chapitre IV, par exemple, dans des
formules du type
FUNCTION ALTER2(X1,X2,PX1)
ALTER2=X2
U=RAN(0)
IF(U.LT.PX1) ALTER2=X1
RETURN
END
où x provient d'une variable aléatoire toujours positive, étant
donc utilisée comme intervalle séparant deux événements
consécutifs. Cette équation pourrait alors se programmer
ainsi :
en faisant usage du sous-programme suivant (IBIDON est un
paramètre bidon, comme son nom l'indique).
ZNEUF=ZVIEUX+(XSIGNE(0)*appel à un canon),
FUNCTION XSIGNE(IBIDON)
XSIGNE=-1.0
U=RAN(0)
IF(U.LT.0.5) XSIGNE=l.0
RETURN
END
3.3.2 Distribution binomiale
Les choix entre deux alternatives exposés ci-dessus sont des
tirages bernoulliens. Une série de n tirages bernoulliens
synthétise une population conforme à la distribution binomiale
B(n, p), où p est la probabilité de l'une des alternatives, appelée
succès. Cette distribution examine a posteriori une série de
tirages bernoulliens, et sa variable aléatoire est le nombre de
succès obtenus au cours des n tirages :
Cette variable aléatoire correspond donc à un point de vue
analytique sur des choix entre deux alternatives.
pour x=0, 1, 2, ..., n, et où
c'est-à-dire le nombre de combinaisons sans répétition de x éléments choisis
parmi n (cf.2 .1, ci-dessus, pour des références sur l'analyse
combinatoire).
3.3.3 Distribution de Poisson
D'autre part, si n devient grand et p petit, on peut montrer que
la distribution binomiale peut être approximée par la distribution
de Poisson, ce qui procure l'avantage d'éliminer n des calculs
([21], pp.307-309, et [22a], pp.153 sq.). Cette
approximation est bonne pour des valeurs de n>50 et de p<0.1 de sorte que le
produit
soit de l'ordre de quelques unités. Ce
paramètre
s'appelle la densité moyenne de la
distribution de Poisson. Ce lien entre les distributions binomiale
et de Poisson implique donc aussi que, pour un grand
(quelque peu supérieur à 20), la formule de Poisson approxime une
distribution de Gauss-Laplace de moyenne
et d'écart type
([21], pp. 330-331, et [22a], pp.190 sq.). Dans de telles conditions, un
algorithme de Poisson pourrait être utilisé comme canon
Gauss-Laplace de nombres entiers -- mais l'avantage
serait mince, étant donné que la distribution de Poisson est
relativement lourde à programmer.
pour x=0, 1, 2,... .
L'énoncé SUBROUTINE POINIT (I ,N,D,TAB,ITOT,NMAX) marque le début
d'une section d'initialisation de la table (TAB) des différentes
F(x) requises. TAB a deux dimensions (ITOT,NMAX), étant
effectivement considérée comme ITOT vecteurs, chacun contenant la
F(x) de la i-ème distribution de Poisson de densité
:
SUBROUTINE POINIT(I,N,D,TAB,ITOT,NMAX)
DIMENSION TAB(ITOT,NMAX)
XKFAC=1 .0
DO 30 J=1 ,N-1
XK=FLOAT(J-1)
IF(XK.LE.1 .0) GOTO 20
XKF AC=XKF AC*XK
20 VAL=((D**XK)/XKF AC) *EXP(-D)
IF(XK .EQ.0 .0) GOTO 25
TAB(I,J)=TAB( I,J-I)+VAL
GOTO 30
25 TAB(I,1)=VAL
30 CONTINUE
TAB(I ,N)=1 .0
RETURN
ENTRY POISSO(I ,N, NBR,TAB,ITOT,NMAX)
U=RAN(0)
DO 1 J=1 ,N
IF(U.LT.TAB(I ,J)) GOTO 2
1 CONTINUE
2 NBR=J-1
RETURN
END
Ces vecteurs doivent être plus ou moins longs, selon les densités
On doit prévoir NMAX de telle sorte que, pour la plus
forte densité utilisée,
soit très petite et puisse être négligée : en effet,
l'algorithme ne peut jamais fournir de résultat plus grand que
NMAX-1.
Le programme principal doit appeler POINIT avec les paramètres
appropriés afin d'initialiser tous les ITOT vecteurs F(x) de TAB.
3.3.4 Choix entre plusieurs alternatives
Lorsque l'ensemble fondamental comprend plus de deux événements de
probabilités données, l'algorithme suivant est nécessaire. On y
explore simplement un cumul des probabilités, afin de désigner un
résultat xs à partir d'un us.
Les paramètres de l'appel sont
FUNCTION ALTERN(BOUL,PROB ,N)
DIMENSION BOUL(N),PROB(N)
SOM=0 .0
U=RAN(0)
DO 1 I=1,N
SOM=SOM+PROB(I)
IF(U .GE .SOM) GOTO 1
ALTERN=BOUL(I)
RETURN
1 CONTINUE
ALTERN=BOUL(N)
RETURN
END
PROB : le nom du vecteur déclaré dans le programme appelant,
contenant la liste des différentes probabilités associées aux
événements de BOUL, de sorte que
N : la dimension de BOUL et de PROB.
ALTERN renvoie le résultat xs=BOUL(I).
Les algorithmes précédents constituaient des cas particuliers de
ce dernier : INRECT lorsque toutes les probabilités sont
égales, et ALTER2 lorsque seulement deux alternatives sont en
présence.
et
ainsi que
3.3.5 Tirages exhaustifs, permutation
Un procédé typiquement sériel serait de choisir des événements d'un
ensemble fondamental sans répétition d'aucun événement avant
épuisement de l'ensemble fondamental ([4], pp.15-17 et
pp.32-34) ; on réaliserait ainsi une permutation des événements
de l'ensemble fondamental. Bien entendu, ce principe reste valable
même si certains des événements disponibles sont identiques -- les
séries dodécaphoniques ne sont qu'un cas particulier :
l'illustration classique de ce processus consiste à imaginer que
l'on tire au hasard des boules de couleurs variées contenues dans
une urne, sans les y replacer après tirage. La configuration
initiale est de N boules, dont n1 de couleur x1,
n2 de couleur x2, etc., de sorte qu'au premier tirage on a
Bien sûr, une fois que la première boule, de couleur xs, est sortie
de l'urne,
et ainsi de suite (cf. [21], pp.103-114).
Le programme principal doit avoir déclaré les deux tables
LENSMB(N) et ITRAV(2,N). Dans l'énoncé d'appel,
SUBROUTINE PERMUT(LENSMB,ITRAV,N,IOPT)
DIMENSION LENSMB(N),ITRAV(2,N)
IC=N
DO 1 I=1 ,N
ITRAV(1,I)=I
1 CONTINUE
2 IX=INRECT(1,IC)
IR=ITRAV(1,IX)
ITRAV(2,IC)=LENSMB(IR)
ITRAV(1,IX)=ITRAV(1,IC)
IC=IC-l
IF(IC.EQ.0) GOTO 3
GOTO 2
3 IF(IOPT.NE.1) RETURN
DO 4 I=1,N
LENSMB(I)=ITRAV(2,I)
4 CONTINUE
RETURN
END
Dans l'algorithme, IC est un compteur, ITRAV(1, J) est utilisé
pour prévenir les répétitions d'événements, et ITRAV(2, J)
emmagasine la permutation en cours d'élaboration. PERMUT fait
appel au canon INRECT (3 .1, ci-dessus). Un ou plusieurs programmes
appelants peuvent très bien utiliser plusieurs ensembles LENSMB,
mais une seule table de travail ITRAV(2, Nmax) serait nécessaire,
où Nmax serait la dimension du plus grand LENSMB.
4 . Lois de probabilité continues
4.1 Distributions uniformes
Sol per te le mie ore son generate.
Comme nous avons eu l'occasion de le voir, la distribution continue
uniforme dans l'intervalle [0, 1] est la base de tous nos
algorithmes, dispensatrice de tout aléatoire (cf. 2 .6 .1, ci-dessus).
Bien sûr, la continuité doit s'entendre comme limitée à la précision
des mots de l'ordinateur utilisé ; mals les précisions
courantes de huit chiffres décimaux ou d'avantage sont assez
adéquates.
Leonardo da Vinci
La disponibilité d'un canon U typique est considérée comme acquise ; si ce n'est pas le cas, il est toujours possible d'en programmer un, moyennant certaines connaissances, ou de s'en procurer un dans la littérature. Les algorithmes de canons U sont étudiés d'un point de vue général dans [13], pp.136-142, [11], pp.1-100, et [12], chapitre 2. Des exemples pratiques peuvent être consultés dans [14], p.77 (pour des mots de trente-deux bits), ou dans [5], p.69 (similaire au précédent, mais pour des mots de vingt-sept (sic) bits). Un algorithme FORTRAN complet, dont l'efficacité ne dépend pas des spécificités de l'ordinateur employé, est présenté dans [15]. L'on doit être conscient du fait que le canon U, deus ex machina par excellence de toute application stochastique, mérite qu'on lui accorde les plus grands soins. Particulièrement dans les cas où l'on fait une grande consommation de nombres aléatoires, seuls des algorithmes fiables et éprouvés devraient mériter notre confiance, afin que l'entreprise soit conséquente.
Conformément au concept même d'algorithme, il est remarquable que ces générateurs aléatoires sont rigoureusement déterministes ; chaque nombre « aléatoire » est élaboré au moyen de manipulations effectuées sur le nombre « aléatoire » précédent, ce qui leur vaut à bon droit l'appellation de pseudo-aléatoires :
Ils génèrent des séquences imperturbables de valeurs enchaînées les unes aux autres. Pour modifier ces séquences, il nous faut modifier le germe de l'algorithme, c'est-à-dire la valeur aléatoireo présente dans le générateur avant son premier appel -- cela peut se faire judicieusement au besoin, ou systématiquement, en donnant comme germe, par exemple, un nombre arbitrairement concocté à partir de la date et de l'heure de l'exécution du programme. Mais ces algorithmes incarnent bien exactement l'ancienne conception épicurienne du hasard comme étant une vue subjective sur une combinaison complexe de causes déterministes échappant à notre entendement : « Le hasard est une cause incertaine quant aux personnes aux temps et aux lieux » (Aetius, ln Épicure et les épicuriens, Paris, P.U.F., 1976, p.72).
Afin d'obtenir une distribution uniforme dans un intervalle autre que [0,1] on utilisera une fonction linéaire de U, exactement comme dans l'algorithme INRECT (3 .1, ci -dessus), mais cette fois sans tronquer le résultat : l'équation
où r1 et r2 sont deux limites réelles (r1<r2), génère une distribution rectangulaire uniforme dans [r1, r2]
On peut égaliser la fonction de répartition de U ((g), 2 .6 .1, ci-dessus),
et la F(x) de la variable désirée :
L'on a alors us, comme fonction de xs, et ceci peut être inversé algébriquement en xs comme fonction de us. Ainsi, us sera transformé en un xs conforme à la distribution recherchée :
([11], pp.102-103, [12], chapitre 3 [13], pp.142-143, [21], chapitre XV).
Ce procédé peut être saisi intuitivement comme l'utilisation du us dans l'intervalle [0,1] pour désigner une fraction de la surface sous la fonction de probabilité désirée ; on déduit ensuite à quel xs correspond cette fraction de surface (cf. figure 4) : il s'agit simplement d'une application plus générale, continue, de la méthode discrète exposée ci-dessus (3. 2).
Toutefois, certaines distributions de probabilité possèdent une
fonction de répartition F(x) qui ne peut être simplifiée
(intégrée) afin de subir cette inversion algébrique. De tels cas
appellent des algorithmes spéciaux : nous en étudierons deux
dans la section 4. 4, ci-dessous.
4.3 Quelques distributions continues d'obtention directe
4.3.1 Distribution linéaire
Cette distribution est décrite par Xenakis([1], p.27 et pp.219sq comme
étant la probabilité de tirer un segment de longueur x
à l'intérieur d'une droite de longueur g, lorsque les deux points
délimitant x sont désignés au hasard (avec une distribution
uniforme) sur la droite [0,g] :
Son histogramme est représente à la figure 12. Cette distribution est équivalente à la moitié droite de la distribution triangulaire décrite dans [22b], p.50.
Le canon se prépare ainsi :
En égalisant avec F(us)=us on obtient l'équation quadratique
qui possède deux racines : dont seulement est utile ici, puisque l'autre ferait toujours xs>g alors que nous devons nous limiter à l'intervalle 0<xs<g. Le terme (1-us) étant simplement un nombre aléatoire de distribution uniforme dans [0,1], symétrique de us par rapport à 0.5, l'on peut simplifier finalement à
Comme le montre l'histogramme (figure 12), les petites valeurs de X sont favorisées, ceci à cause de la relation qui tend à rapprocher toujours de zéro.
La distribution exponentielle de densité moyenne (intervalle moyen = ) est
La fonction de répartition est
Par égalisation avec F(us), l'on obtient
que l'on inverse en
Comme ci-dessus, l'on peut finalement simplifier en
Des histogrammes de la distribution exponentielle, pour trois densités différentes, sont représentés figure 13.
où est la fonction eulérienne gamma :
La distribution exponentielle de densité 1 (f(x)=e-x) est un cas particulier de la distribution gamma, pour v=1. Des histogrammes de la distribution gamma, pour trois v différents, sont représentés figure 14. Ils démontrent l'intérêt particulier de cette distribution : son asymétrie. Les plus fortes probabilités (le mode, en terminologie statistique) sont pour les valeurs de X proches de v-1, tandis que la moyenne de cette distribution est v ([21], p.350). Dans des applications rythmiques, elle peut produire une espèce de délié par rapport à l'exponentielle -- oserait-on dire : rubato ? (cf. section 5, ci -dessous).
On ne peut arriver à une formule permettant l'obtention directe de variables aléatoires gamma pour toutes valeurs réelles de v. Si nécessaire, un algorithme capable de cette performance est décrit dans [17], pp.13-15 ; mais il n'est pas si simple... En lui-même, il requiert le canon gamma restreint à des v entiers, décrit ci-dessous, plus un canon beta (cf. 4 .4 .2). Autrement, un algorithme d'approximation, analogue au premier canon beta exposé en 4 .4 .2, serait nécessaire.
Mais l'on peut démontrer l'égalité suivante pour des variables aléatoires gamma indépendantes de paramètres v et w ([21], pp.200-201) :
Pourvu que l'on se satisfasse de valeurs entières du paramètre v, l'on peut donc synthétiser une variable aléatoire en faisant la somme de v variables indépendantes :
Cette restriction n'est pas prohibitive, puisque l'on pourra toujours, après coup, multiplier la variable obtenue par un facteur quelconque , afin de situer le mode à et la moyenne à , ou même élaborer une fonction linéaire ([21], p. 352).
La formule-canon pour la variable , (exponentielle, avec =1) étant
Il nous suffira d'additionner des xs successifs v fois dans une boucle. En vertu de l'égalité
l'algorithme peut éviter de faire appel v fois à la fonction ALOG.
Cette méthode est décrite dans [11], p.115 (pour la distribution khi-carré (X2), proche de la gamma), et dans [17], pp.11-12.FUNCTION GAMMA(NU) SOM=1 .0 DO 1 N=1 ,NU SOM=SOM*RAN(0) 1 CONTINUE GAMMA=-ALOG(SOM) RETURN END
Un histogramme de cette distribution est représenté figure 15. Elle possède l'intérêt d'être une distribution symétrique centrée sur une moyenne, c'est-à-dire que l'abscisse du mode central est égale à la moyenne, mais d'une allure différente de celle de la plus banale distribution normale (4 .4 .1 ci-dessous).
La fonction de répartition est
En égalisant avec us et en scindant les résultats de sorte que
les deux formules suivantes réalisent la distribution :
Dans l'algorithme ci-dessous, l'on introduit deux paramètres d'appel, afin de générer directement une fonction linéaire de X :
peut être une moyenne autre que zéro, et est un paramètre affectant la dispersion (ambitus, ou « étalement horizontal ») de la distribution. Ainsi, notre algorithme génère effectivement la variable
FUNCTION PLAPLA(XMU,TAU) Y=RAN(0)*2.0 IF(Y.GT.1.0) GOTO 1 PLAPLA=(TAU*ALOG(Y))+XMU RETURN 1 Y=2.0-Y PLAPLA=(-TAU*ALOG(Y))+XMU RETURN END
Dotée d'un paramètre réglant la dispersion de la variable aléatoire, la distribution de Cauchy est
La fonction de répartition est
à partir de laquelle on obtient la formule-canon :
Le canon fonctionne donc en prenant la tangente d'un angle entre /2 et /2. Afin d'optimiser notre algorithme, nous pouvons aussi bien prendre la tangente d'un angle entre 0 et cela nous permet d'arriver à cette formule finale :
Cette équation rend intuitivement tangible l'absence de moyenne de la distribution de Cauchy : l'on sait que la tangente d'un angle proche de /2 est extrêmement grande ; puisque peut désigner un tel angle avec autant de probabilité que tout autre, de très grandes valeurs de X sont encore assez probables, et peuvent « déséquilibrer » une éventuelle tendance de la distribution vers une moyenne.
Une version modifiée de la distribution de Cauchy sera générée si le paramètre d'appel IOPT, de l'algorithme ci-dessous, est égal à 1 : seules des valeurs positives seront produites, conformes en fait à la distribution suivante :
Cette version possède à tout le moins un intérêt rythmique certain : elle peut générer des agrégats de points temporels très danses et irréguliers, parsemés dans des intervalles relativement énormes (cf.section 5, ci-dessous). Pour le compositeur, elle peut impliquer le risque de décourager certains auditeurs par des trous de quelques minutes entre deux sons successifs, mais elle peut parfaitement être utilisée avec quelques précautions poétiques... Quoiqu'il en soit, la distribution authentique de Cauchy, symétrique par rapport à zéro, a été utilisée par Xenakis dans des applications à la micro-composition ([3], chapitre IX), à titre de source de dissymétries radicales.
FUNCTION CAUCHY(TAU,IOPT) DATA PI/3.141592654/ U=RAN(0) IF(IOPT.EQ.1) U=U/2.0 U=PI*U CAUCHY=T*(SIN(U)/COS(U)) RETURN END
La fonction de répartition étant
l'on peut aisément arriver au canon suivant :
La figure 18 montre son histogramme : il s'agit encore d'une distribution symétrique, avec un mode pour d'ordonnée (« hauteur »)
pour tout x ou
et pour
Les paramètres et contrôlent ainsi à la fois la moyenne et la dispersion de la distribution (la dispersion est inversement proportionnelle à ).
La fonction de répartition ([22b], p.52) est
qui peut être inversée en la formule-canon
Les distributions cosinus hyperbolique et logistique ont toutes deux été utilisées par Xenakis en micro-composltion ([3], chapitre IX).
afin de la faire couvrir un intervalle quelconque [r1, r2]. La fonction de probabilité est
La fonction de répartition étant
elle noue livre le canon
(a)Par contre, [22b], p.50, donne comme formule :
ce qui revient au même, mais cette seconde formule donne le canon suivant :
(b)Un algorithme réalisant (b) comporterait trois multiplications, tandis que la formule (a), avec deux multiplications et deux soustractions, est à même de nous faire économiser quelques microsecondes -- la vie est courte.
et nomme distributions de Gauss-Laplace les application concrètes de la distribution normale, dotée d'une moyenne et d'un écart type quelconques. On peut concevoir une distribution de Gauss-Laplace soit comme une fonction linéaire d'une variable normale :
soit comme la fonction complète.
Nous avons adopté cette terminologie.
L'importance théorique de la distribution normale a déjà été signalée (3. 3. 3). C'est la distribution classique, en forme de « cloche », représentée à la figure 3. Statistiquement, elle rend compte d'un grand nombre de phénomènes, à cause de ses bases et de son rôle théorique très fondamentaux, ce qui justifie bien son « allure naturelle » : elle présente des probabilités relativement fortes pour la moyenne, et près de la moyenne, un mode arrondi, une moelleuse atténuation des probabilités de valeurs disparates par rapport à la moyenne, etc. La figure 20 illustre certaines caractéristiques de cette distribution très importante. Notez, par exemple, que la probabilité de valeurs hors de l'intervalle est , et hors de est inférieure à 0.003. Des tables de valeurs de f(x) et F(x) sont annexées à tout ouvrage respectable sur les probabilités.
En dépit de sa grande noblesse, nous sommes libres d'utiliser la distribution de Gauss-Laplace en toute liberté. Par exemple, Xenakis l'a utilisée pour des durées ([1], p.174) et pour ses fameuses textures de glissandi (Pithoprakta 1955-56, en particulier, cf. [1], pp.27sq., etc. et [7], pp.243sq.) par analogie avec la distribution de Maxwell-Boltzmann, rendant compte des vitesses tridimensionnelles de molécules dans un gaz (voir aussi [22b], pp.29-32).
À cause de certaines propriétés mathématiques (il est impossible d'extraire l'ntégrale de F(x), pour ainsi dire), il n'existe pas de formule-canon simple pour la distribution de Gauss-Laplace, et l'on doit recourir à des approximations. L'algorithme décrit ici est esquissé dans [13], p.143, et développé dans [14], p.77. Il est basé sur la formule suivante, déduite du théorème central limite (cf. [20], pp. 91-92, par exemple, où ce théorème est énoncé sous une forme similaire à cette formule) : :
où les ui, sont, comme d'habitude, des valeurs aléatoires uniformes dans l'ntervalle [0,1], et où X tend vers une distribution normale lorsque k tend vers l'infini. Un compromis, qui a l'avantage d'alléger l'algorithme, consiste à adopter k=12 : la formule simplifiée est alors :
L'ajustement aux et désirés se fait comme
en fonction linéaire de cette variable aléatoire.
L'efficience de cet algorithme laisse à désirer : douze appels au canon U sont requis pour chaque valeur aléatoire gaussienne ; mais sa simplicité est assez séduisante. Dans des cas où la rapidité d'exécution serait cruciale, il serait peut-être préférable d'utiliser une table de la fonction de répartition F(x), dans un processus similaire au premier algorithme donné ci-dessous pour la distribution beta (4. 4. 2) -- la table pouvant être calculée par l'algorithme, bien entendu, ou repiquée dans un manuel et introduite à titre de données ([21], p.455, [22a], p.176, par exemple). On peut mettre au point des méthodes plus efficaces qu'un simple balayage pour explorer cette table, on peut réduire la taille de la table, et donc les temps de recherche, en se fiant d'avantage à l'interpolation, etc.FUNCTION GAUSS(XMU,SIGMA) S=0.0 DO 1 I=1, 12 S=S+RAN(0) 1 CONTINUE GAUSS=((S-6.0)*SIGMA)+XMU RETURN END
où B(a,b) est la fonction eulérienne beta :
pour 0<x<1
et a>0, b>0,
Selon différentes valeurs des paramètres, les histogrammes de la distribution beta peuvent épouser diverses formes : en cloches plus ou moins symétriques, exponentielles croissantes ou décroissantes (voyez des graphes dans [21], p.358, ou [20], p.97). Toutefois, nous nous limiterons aux cas où a<1 et b<1, à cause des distributions très intéressantes qu'impliquent ces valeurs : des histogrammes en forme de « U » plus ou moins symétriques. La figure 21 illustre quelques cas : le « creux » de la distribution est inversement proportionnel à a vers 1, et à b vers 0. Pour a=b=1, on obtient la distribution continue uniforme à titre de cas particulier.
Pour a=b=0.5, on obtient une distribution arc sinus (cf. 4. 3. 8).
Pour mettre un canon au point, nous utiliserons une table de F(x). L'algorithme suivant peut gérer plusieurs distributions beta de couples de paramètres (a, b) différents ; pour le i-ème couple (a,b)i, on y prépare une table d'approximations de F(x), x croissant en vingt pas de 0.05 entre 0 et 1 :
Afin de calculer le facteur
pour (a, b)i.
nous aurons recours à la propriété
(cf. 4 .3 .3 pour une définition de (a)). Nous pourrons donc utiliser la fonction FGAMMA(Z) ci-dessous pour ce calcul , et ensuite approximer F(x) pas à pas avec un micro-incrément dx=1.25*104 :
Pour les besoins de la TABL (i,n) on ne retiendra cependant que les vingt valeurs obtenues tous les quatre cents micro-incréments : 400dx=0.05. Cette initialisation est faite dans la première partie du sous-programme (SUBROUTINE BEINIT...) ; elle implique bien entendu un temps de calcul important -- mais les tables résultantes peuvent être stockées à part, et récupérées rapidement lors d'utilisations ultérieures.
Les appels destinés à obtenir effectivement une valeur aléatoire doivent utiliser l'ENTRY BETA. De façon analogue au cas de la distribution discrète de Poisson, on utilise alors un us comme pointeur « tombant » quelque part entre deux valeurs de la table de F(x) ; une interpolation linéaire simule ensuite la continuité.
Les paramètres d'appel à BEINIT sontSUBROUTINE BEINIT(NORDR,XA,XB,TABL,NTOT) DIMENSION TABL(NTOT,21) DATA DX/12SE-6/ AB=XA+XB SBETA=FGAMMA(AB)/(FGAMMA(XA)*FGAMMA(XB)) TABL(NORDR,1)=0.0 SOM=0.0 X=-625E-7 A=XA-1.0 B=XB-1.0 DO 30 I=2,20 DO 20 J=1,400 X=X+DX PX=(X**A)*((1.0-X)**B)*SBETA SOM=SOM+(PX*DX) 20 CONTINUE TABL(NORDR,I)=SOM 30 CONTINUE TABL(NORDR,21)=1.0 RETURN ENTRY BETA(NORDR,XX,TABL.NTOT) U=RAN(0) DO 5O K=2,21 IF(U.LT.TABL(NORDR,K)) GOTO 55 50 CONTINUE 55 Z=TABL(NORDR, (K-1)) DS=U-Z DB=TABL(NORDR, K)- Z XX=0.05*((DS/DB)+(K-2) RETURN END
Mais, de par l'égalité
on peut aussi l'utiliser pour z tout court, où
Après le calcul des tables F(x), l'algorithme beta précédent est assez efficace : il requiert un appel au canon U, une recherche dans une table, et une interpolation linéaire. Cependant, il manque certainement d'élégance... Nous l'avons décrit néanmoins, principalement à titre d'exemple destiné à illustrer les cas où le recours à une table et à l'interpolation seraient inévitables ou d'une efficience supérieure extensive de la distribution de Gauss-Laplace, par exemple (4. 4 .1). Jöhnk a conçu cependant un canon beta très astucieux ([17], pp.9-10), valable pour tous paramètres positifs réels a et b, et sans la faiblesse théorique de l'approximation.FUNCTION FGAMMA(Z) DIMENSION C(7) DATA C/-57710166E-8, 98585399E-8, 1 -87642182E-8, 8328212E-7, -5684729E-7, 1 25482049E-8, -514993E-7/ X=Z IFL=0 IF(X.LT.1.0) GOTO 1 X=X-1.0 IFL=1 1 R=1.0 DO 2 I=1,7 R=R+(C(I)*(X**I)) 2 CONTINUE FGAMMA=R IF(IFL.EQ.0) FGAMMA=R/X RETURN END
L'efficience de ce dernier algorithme est intéressante, du moins pour les valeurs de paramètres qui nous intéressent (a<1 et b<1) : dans de tels cas, S=Y1+Y2 a de bonnes chances de ne pas être supérieur à 1, puisque les exposants EA et EB sont plus grands que 1 ; ainsi Y1 et Y2 sont encore plus petits que les u qui les génèrent. Pour a=b=0.75, une moyenne de 3.15 appels à RAN sont nécessaires ; et 2.55 appels lorsque a=b=0.5.FUNCTION BETA (A,B) EA=1.0/A EB=1.0/B 1 Y1=RAN(0)**EA Y2=RAN(0)**EB S=Yl+Y2 IF(S.GT.I.0) GOTO 1 BETA=Y1/S RETURN END
L'action n'est possible que dansDans le but de comparer les cinq distributions symétriques avec mode central que nous avons présentées (première loi de Laplace, de Cauchy, cosinus hyperbolique, logistique et de Gauss-Laplace), nous pouvons les astreindre à une caractéristique commune. Par exemple, on peut doser leurs dispersions au moyen d'un facteur multiplicatif. Comme point de départ, prenons BLOCKQUOTE> de la distribution normale la probabilité de valeurs supérieures à 3 est 1-y=0.00135. Nous centrerons aussi les autres distributions sur zéro, et réglerons leurs dispersions de manière à satisfaire cette condition. Le calcul des facteurs de dispersion nécessaires se fait simplement en remplaçant, dans les formules-canons, xs par 3 et us par y=0.99865, et en résolvant les équations.
une certaine insouciance et la vie
n'est qu'un acte de confiance en
nous-mêmes et dans la bienveillance
des hasards.
Rémy de Gourmont
L'on obtient, pour la première loi de Laplace :
pour la distribution de Cauchy :
pour la cosinus hyperbolique :
logistique (avec , afin de disposer la moyenne à 0) :
La figure 22 montre les moitiés droites des histogrammes résultants, avec les facteurs de dispersion appropriés. La distribution de Cauchy n'est pas illustrée, parce qu'elle ne pourrait être représentée à la même échelle que les autres : avec le ci-dessus, elle donne
un mode vertigineusement abrupt. Autrement, la figure parle d'elle-même : chacune des distributions laisse voir une certaine « personnalité », une certaine allure, et leurs différences pourraient être exploitées afin de modeler, par exemple, les hauteurs de « nuages » de sons d'aspects variés, plus ou moins concentrés sur leur hauteur moyenne -- bien entendu, une grande quantité de valeurs aléatoires seraient nécessaires pour affirmer des caractéristiques aussi franches que les promettent les histogrammes.
Les variables aléatoires générées par la distribution gamma -- y incluse l'exponentielle -- et la distribution linéaire, peuvent être utilisées pour des intervalles séparant des points dans le temps, par exemple. Encore une fois, chaque distribution affirme une personnalité.
Afin de rendre la comparaison probante, toutes les séquences d'intervalles aléatoires de temps devraient être ajustées à la même moyenne : nous choisissons arbitrairement e=2.71928... points par seconde. La moyenne de la distribution linéaire, de paramètre g, est g/3. En faisant g= 3/e l'on produira l'intervalle moyen 1/e, c'est-à-dire e points par seconde. Le canon exponentiel, pour sa part, sera directement appelé avec Pour ce qui est de la distribution gamma, l'on sait que la moyenne d'une variable est v ; afin de régler cette moyenne à 1/e, l'on doit faire
Nous avons choisi de tester cette distribution (y comprise l'exponentielle comme ) avec v=1, 2, 4, 8, 16. Il s'avère que cette progression exponentielle de v a pour effet, à la perception, une régularisation rythmique d'apparence plutôt linéaire. La régularisation elle-même est évidemment due au fait que la distribution gamma perd son asymétrie pour de grandes valeurs de v.
La figure 23, de (b) à (f) , fait voir cette comparaison. Chaque rectangle de la figure représente quarante unités de temps, réparties sur trois lignes, et la densité moyenne de points par unité est chaque fois très proche de e (moins de 2% de différance). De (b) à , l'accroissement de symétrie est évident. La distribution linéaire (a) produit un effet en quelque sorte intermédiaire entre la et la Pour le plaisir de la comparaison, le rectangle (g) montre une distribution de Cauchy d'intervalles (obtenue avec IOPT=1 dans l'algorithme de 4 .3 .5) qui ont été ajustés a posteriori à la même moyenne de e points par unité : l'irrégularité de cette distribution semble relever véritablement d'un imprévisible totalement « inhumain », et il n'est pas de romantique tentative de la dompter avec un paramètre de dispersion qui puisse surmonter le fait mathématique qu'elle n'a pas de moyenne prévisible. Ce rectangle (g) de la figure 23 a été choisi à titre d'illustration d'une espèce d'asymétrie maximale acceptable ; il serait difficile d'en permettre d'avantage dans un tel contexte.
De même, dans des applications rythmiques, la distribution beta, y comprise la distribution continue uniforme comme étant le cas particulier , peut faire l'effet d'une progression intéressante. La moyenne d'une distribution est
Puisque l'on veut encore comparer différentes distributions avec une densité moyenne commune de e points par unité, un facteur multiplicatif devra être appliqué aux valeurs aléatoires qui seront générées dans l'intervalle [0,1] par le canon, afin d'amener l'intervalle moyen à 1/e ; l'équation suivante fait cet ajustement :
L'on a alors des cas (figure 24) d'intervalles de temps dans l'intervalle fini
Dans nos exemples, puisque nous avons toujours utilisé a=b, l'intervalle est effectivement [0,2/e]. Relativement à la figure 23, on réalise une plus grande homogénéité, même dans le rectangle (a), à cause de la présence d'une limite supérieure à la longueur des intervalles (2/e), qui se traduit par l'émergence d'une espèce de pulsation de base ; et les intervalles plus courts semblent-être perçus comme des subdivisions de ce quasi-tempo. Dans (a), puisque la distribution favorise considérablement les valeurs proches de 0 et de 1, l'on remarque de nombreuses configurations de type
avec des nombres variés de « petites notes ». De (a) à (e), la prédominance de cette caractéristique s'estompe, puisque des valeurs moyennes deviennent de plus en plus probables, jusqu'à atteindre l'équiprobabilité totale en (e).
Les comparaisons et applications précédentes n'ont la prétention que d'exemples et de suggestions. Une fois définis ces canons stochastiques, le problème crucial demeure, d'appliquer ces variables aléatoires à des phénomènes musicaux. Il n'y a pas de limite à l'utilisation de variables stochastiques en musique. Par exemple, les points de la figure 23 pourraient bien être lus comme des listes de hauteurs sélectionnées sur un axe de fréquences, destinées à des développements ultérieurs. Les durées des sons attaqués aux points de cette même figure 23 pourraient être contrôlées par quelque distribution symétrique à mode central, ou éventuellement par des distributions asymétriques aussi, mais chaque fois différentes de celles générant les intervalles entre les attaques, etc.
Au-delà de ces applications directes et statiques, il est possible de concevoir des mécanismes de transitions -- stochastiques elles-mêmes, éventuellement -- entre différentes distributions ; ou encore des méthodes de contrôle stochastique des paramètres de distributions, qui exploiteraient plusieurs niveaux d'interdépendance, etc.
Si la théorie des probabilités est bien une réponse à des problèmes de choix, il reste encore beaucoup à choisir... reste à faire face à la musique.
d.l. ____________________________ ____________________________
Paris, Montréal
10/79-6/80
Figures
Figure 1 - Histogramme de l'urne du §2.2
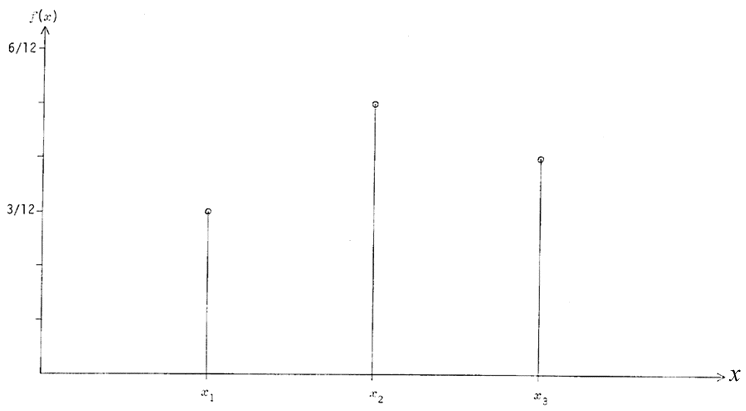
Figure 2 - Fonction de répartition de l'urne du §2.2
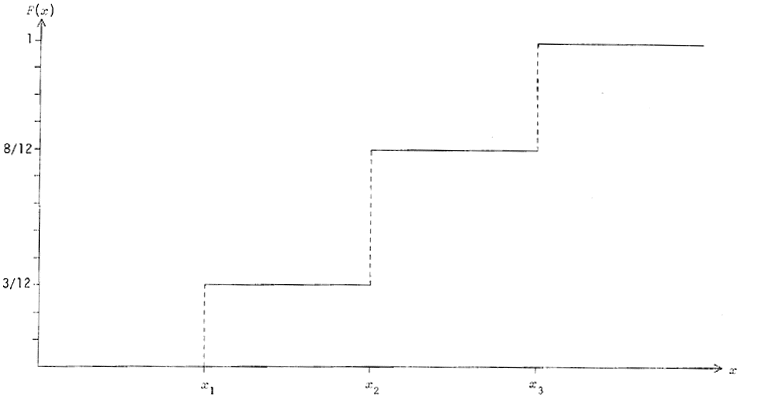
Figure 3 - Histogramme d'une distribution continue (la distribution normale).
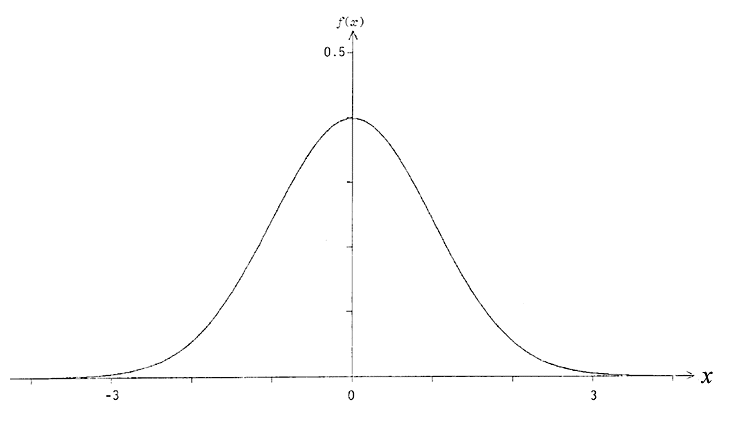
Figure 4 - La fonction de répartition comme la surface sous la fonction de probabilité : l'aire
hachurée est
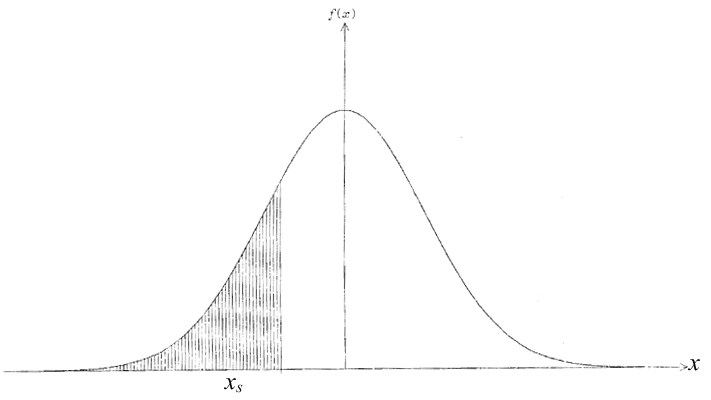
Figure 5 - La surface du rectangle mesurant f(xs)
par dx est la probabilité que X prenne une valeur dans l'intervalle dx autour de xs.
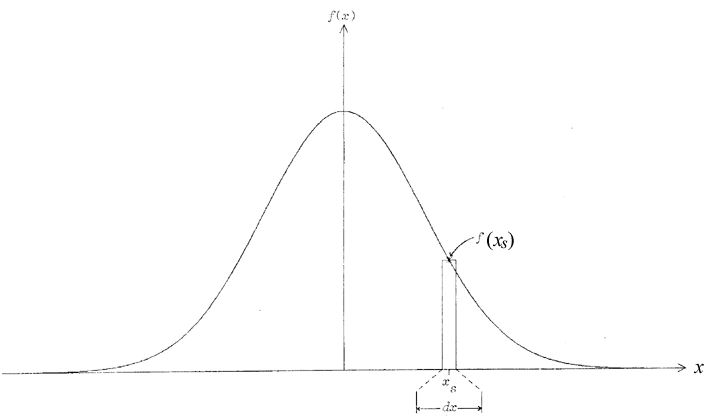
Figure 6 - Histogramme de la distribution continue uniforme U.

Figure 7 - Fonction de répartition de la distribution continue uniforme U.
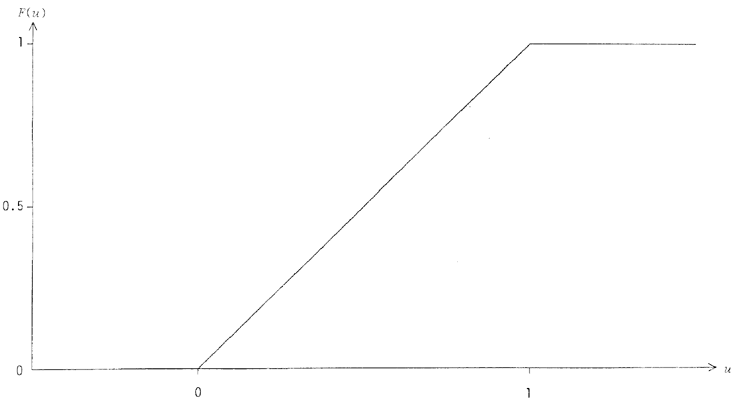
Figure 8 - Histogramme de la distribution uniforme discrète.
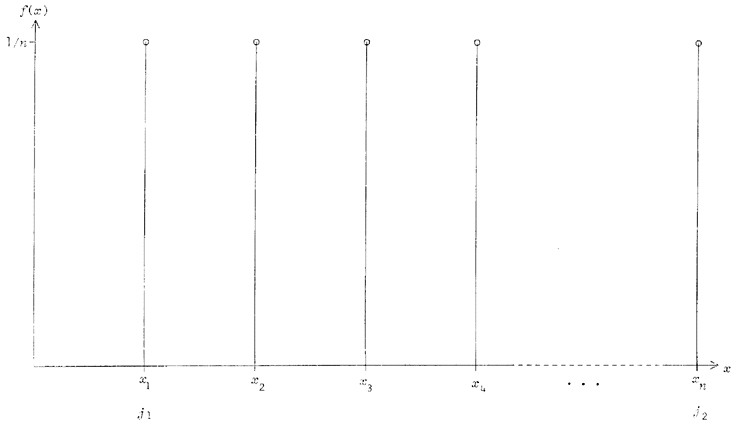
Figure 9 - P{X=x} comme des segments de droite dans l'intervalle [0,1].

Figure 10 - Histogramme de la distribution binomiale B(50,0.05).
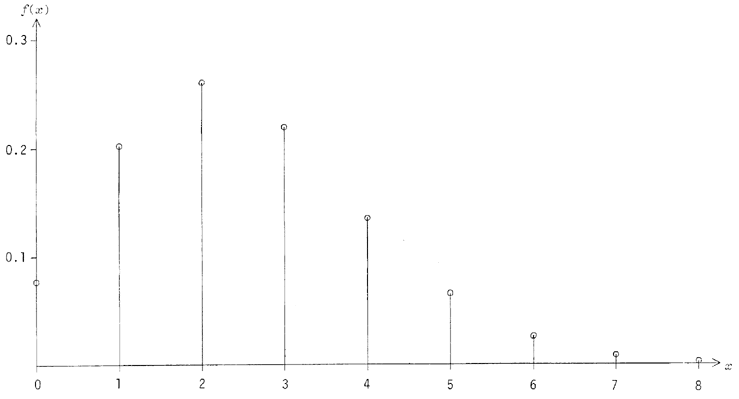
Figure 11 - Histogramme de la distribution de Poisson pour
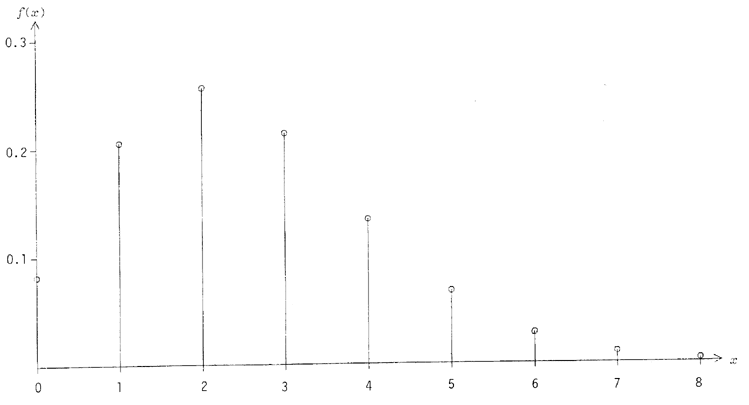
Figure 12 - Histogramme de la distribution linéaire, de paramètre g.
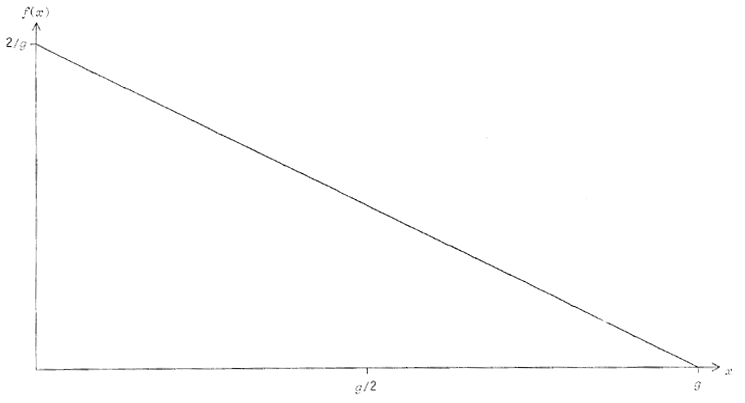
Figure 13 - Histogramme de la distribution exponentielle, pour différentes valeurs de
.
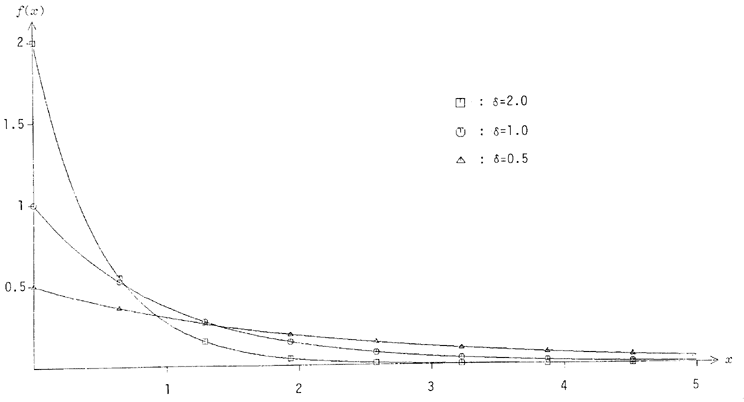
Figure 14 - Histogrammes de la distribution gamma, pour différentes valeurs de v.
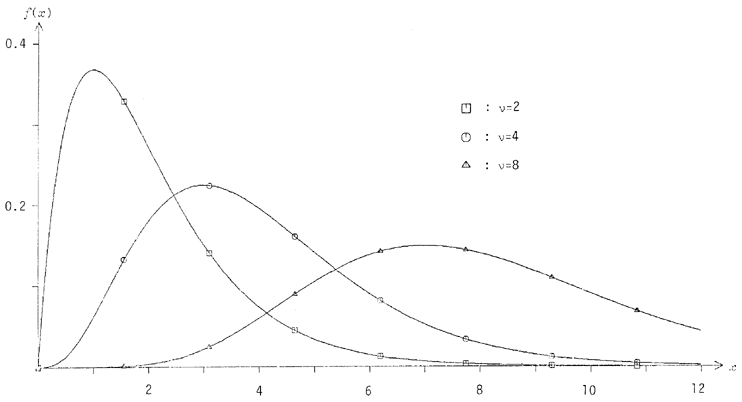
Figure 15 - Histogramme de la première loi de Laplace (avec nos paramètres
et
).
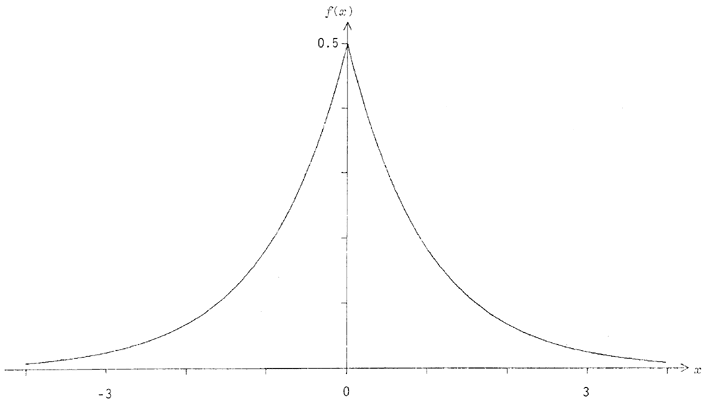
Figure 16 - Histogramme de la distribution de Cauchy
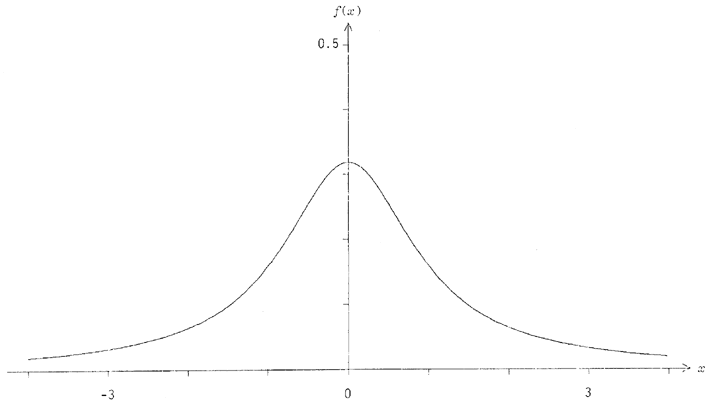
Figure 17 - Histogramme de la distribution cosinus hyperbolique.
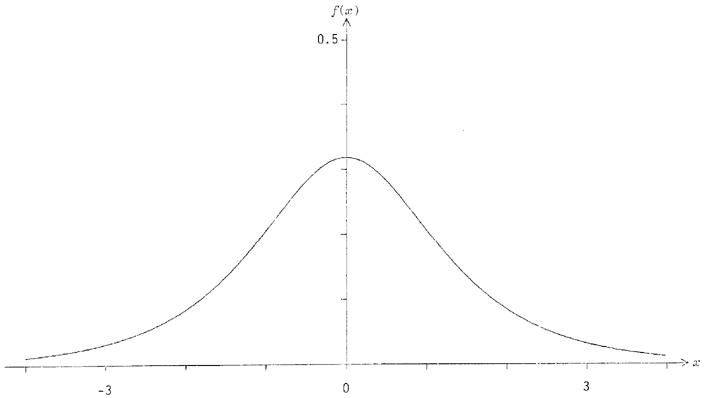
Figure 18 - Histogramme de la distribution logistique pour
(moyenne 0) et
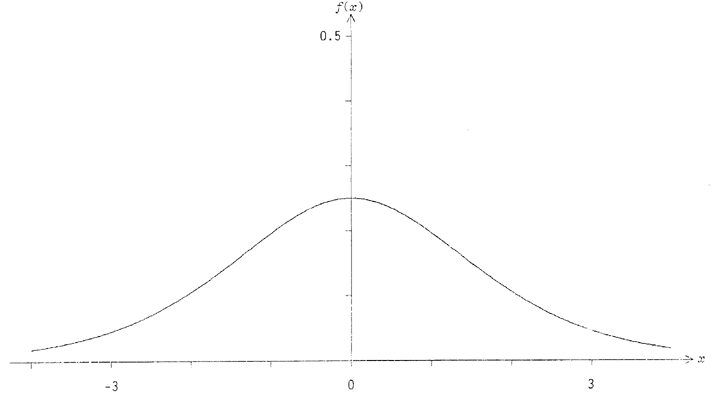
Figure 19 - Histogramme de la distribution arc sinus.
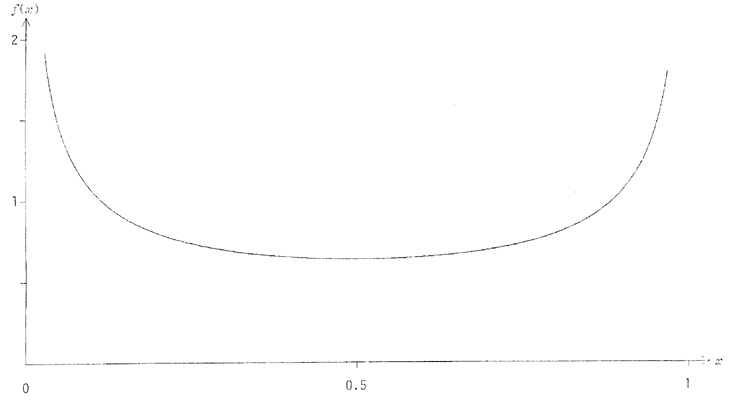
Figure 20 - Histogramme de la distribution normale
Quelques caractéristiques importantes sont représentées. Les pourcentages sont de la surface sous f(x).
([22a]), p.178).
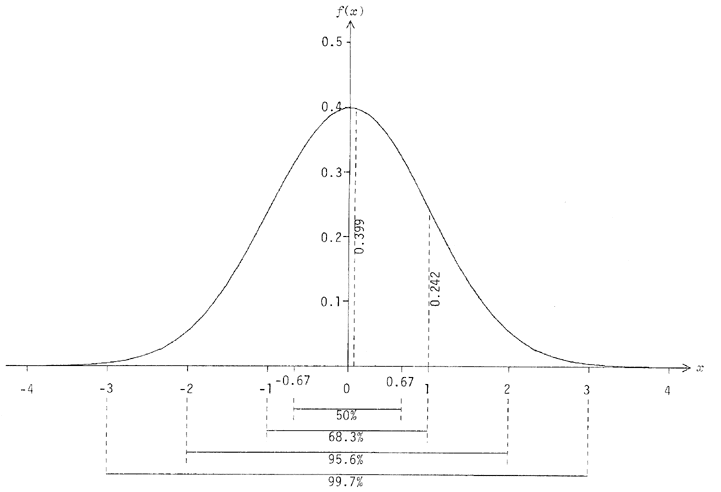
Figure 21 - Histogrammes de la distribution beta, pour quatre différents couples
de paramètres(a, b).
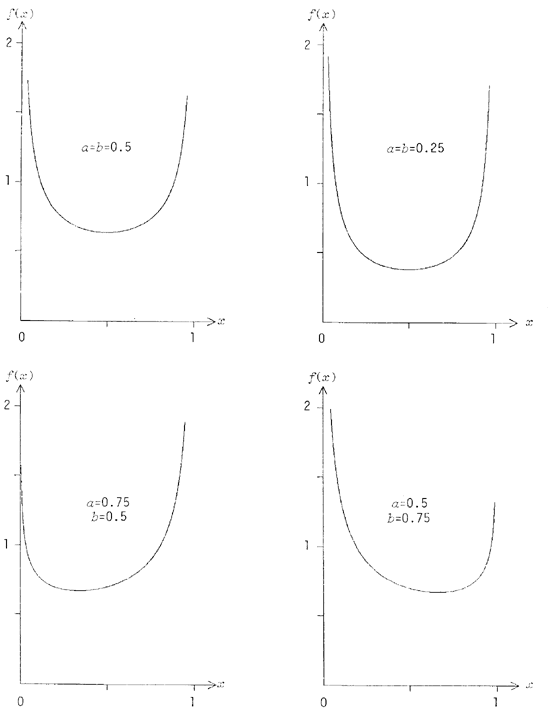
Figure 22 - Moitiés droites des histogrammes de quatre distributions,
toujours ajustées de sorte que F(3)=0.99865.
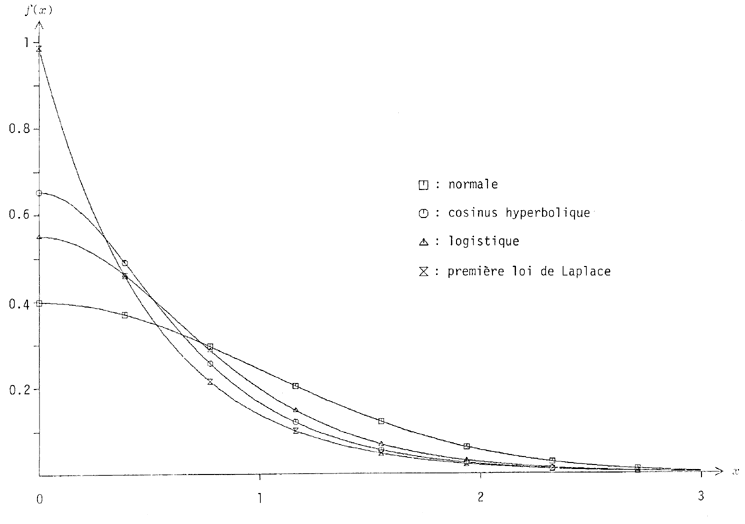
Figure 23 - La même densité moyenne générée par différentes distributions :
(a) linéaire,
(b)
(exponentielle), (c)
(d)
(e)
(f)
(g) de Cauchy ajustée (voir section 5). Un X représente un « point » on a fait
usage de rotations de ce symbole afin de rendre quelque peu visibles des agrégats de deux ou plusieurs
points rapproché, superposés à cause de l'exiguïté de la figure. Il y a trois lignes de points
par rectangle, représentant un total de quarante unités.

Figure 24 - La même densité moyenne réalisée par différentes variables beta :
(a)
(b)
(c)
(d)
(e)
équivalente à la distribution
continue uniforme. Un X représente un « point » ; on a fait usage de rotations de ce
symbole afin de rendre quelque peu visibles des agrégats de deux ou plusieurs points
rapprochés, superposés à cause de l'exiguïté de la figure. Il y a trois lignes de points par
rectangle, représentant un total de quarante unités.

Bibliographie
Ouvrages musicaux et généraux
Canons
Théorie des probabilités
b. Feller, William. An Introduction to Probability Theory and
Its Applications, vol. II, John Wiley, N.Y., 1971
Théorie des probabilités
Server © IRCAM-CGP, 1996-2008 - file updated on .
Serveur © IRCAM-CGP, 1996-2008 - document mis à jour le .